Расчет параметров входного фильтра

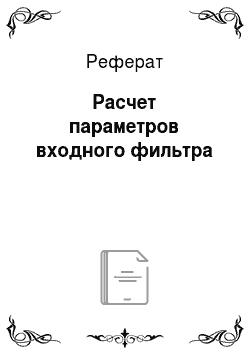
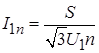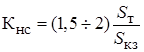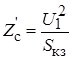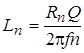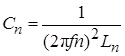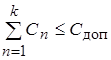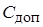При расчете параметров входного фильтра, представленного на рис. 7, исходят из того, что коэффициент несинусоидальности напряжения.

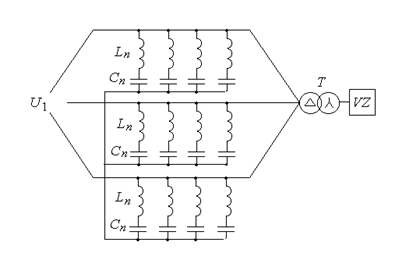
Рис. 7. Схема входных фильтров

определяется первыми четырьмя каноническими гармониками тока.

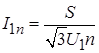
(17).

где n — номер гармоники входного тока, зависящий от числа фаз выпрямителя, n=km+1, где m — число фаз выпрямителя (3 или 6); k — целое число (1, 2, 3 и так далее).

Коэффициент несинусоидальности при отсутствии фильтра будет примерно равен.

Расчет каждого контура начинают с определения активного сопротивления индуктивности контура (рис.7), настроенного на данную гармонику.

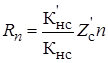
(18).

где — сопротивление системы внешней сети, приведенное к входному напряжению, т. е. ко входу силового трансформатора, где устанавливаются фильтры.

. (19).

Задаваясь добротностью контура Q, определяем значение.

и затем значение емкости контура.

.

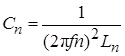
Так как входной фильтр не только снижает высшие гармоники, но и компенсирует реактивную мощность выпрямителя, то для того чтобы не возникла нежелательная перекомпенсация, необходимо на суммарную емкость контуров наложить дополнительное условие.

. (20).

определяется по мощности выпрямителя.

.

где при f=50 Гц.

При cos выпрямителя 0,93 — 0,95 sin= 0,37 — 0,31.

В результате следует привести полную схему рассчитанного выпрямителя. Пример такой схемы приведен на рис. 8.

Оформляется контрольная работа в виде пояснительной записки с рисунками и чертежами на листах писчей (желательно в клеточку) бумаги формата А4 с полями и только на одной стороне листа.

Записка должна содержать титульный лист, задание, расчеты и рисунки согласно заданию, заключение и список использованной литературы.