Сущность двухшагового метода наименьших квадратов

Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.

Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.

История До начала XIX в. учёные не имели опредёленных правил для решения системы уравнений, в которой число неизвестных менее числа уравнений; до этого времени употреблялись частные приёмы, зависевшие от вида уравнений и от остроумия вычислителей, и потому разные вычислители, исходя из тех же данных наблюдений, приходили к различным выводам. Лежандру (1805−06) и Гауссу (1794−95) принадлежит первое применение к решению указанной системы уравнений теории вероятности, исходя из начал, аналогичных с началом арифметической середины, уже издавна и, так сказать, бессознательно применяемых к выводам результатов в простейшем случае многократных измерений. Как и в случае арифметической середины, вновь изобретённый способ не даёт, конечно, истинных значений искомых, но даёт зато вероятнейшие значения. Этот способ распространён и усовершенствован дальнейшими изысканиями Лапласа, Энке, Бесселя, Ганзена и др. и получил название метода наименьших квадратов, потому что после подстановки в начальные уравнения неизвестных величин, выведенных этим способом, в правых частях уравнений получаются если и не нули, то небольшие величины, сумма квадратов которых оказывается меньшей, чем сумма квадратов подобных же остатков, после подстановки каких бы то ни было других значений неизвестных. Помимо этого, решение уравнений по способу наименьших квадратов даёт возможность выводить вероятные ошибки неизвестных, то есть даёт величины, по которым судят о степени точности выводов.

Постановка задачи Задача метода наименьших квадратов состоит в выборе вектора, минимизирующего ошибку. Эта ошибка есть расстояние от вектора до вектора. Вектор лежит в простанстве столбцов матрицы, так как есть линейная комбинация столбцов этой матрицы с коэффициентами. Отыскание решения по методу наименьших квадратов эквивалентно задаче отыскания такой точки, которая лежит ближе всего к и находится при этом в пространстве столбцов матрицы. Таким образом, вектор должен быть проекцией на пространство столбцов и вектор невязки должен быть ортогонален этому пространству. Ортогональность состоит в том, что каждый вектор в пространстве столбцов есть линейная комбинация столбцов с некоторыми коэффициентами, то есть это вектор. Для всех в пространстве, эти векторы должны быть перпендикулярны невязке :

Так как это равенство должно быть справедливо для произвольного вектора, то решение по методу наименьших квадратов несовместной системы, состоящей из уравнений с неизвестными, есть уравнение которое называется нормальным уравнением. Если столбцы матрицы линейно независимы, то матрица обратима и единственное решение Проекция вектора на пространство столбцов матрицы имеет вид Матрица называется матрицей проектирования вектора на пространство столбцов матрицы. Эта матрица имеет два основных свойства: она идемпотентна,, и симметрична,. Обратное также верно: матрица, обладающая этими двумя свойствами есть матрица проектирования на свое пространство столбцов.

Примеры Пусть надо решить систему уравнений.

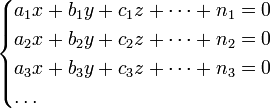
(1).

число которых более числа неизвестных x, y, Чтобы решить их по способу наименьших квадратов, составляют новую систему уравнений, число которых равно числу неизвестных и которые затем решаются по обыкновенным правилам алгебры. Эти новые, или так называемые нормальные уравнения составляются по следующему правилу: умножают сперва все данные уравнения на коэффициенты у первой неизвестной x и, сложив почленно, получают первое нормальное уравнение, умножают все данные уравнения на коэффициенты у второй неизвестной y и, сложив почленно, получают второе нормальное уравнение и т. д. Если означить для краткости:

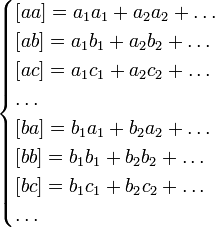
то нормальные уравнения представятся в следующем простом виде:

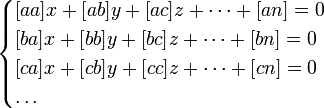
(2).

Легко заметить, что коэффициенты нормальных уравнений весьма легко составляются из коэффициентов данных, и притом коэффициент у первой неизвестной во втором уравнении равен коэффициенту у второй неизвестной в первом, коэффициент у первой неизвестной в третьем уравнении равен коэффициенту у третьей неизвестной в первом и т. д. Для пояснения сказанного ниже приведено решение пяти уравнений с двумя неизвестными:

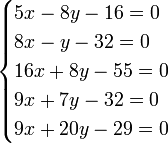
Составив значения [aa], [ab], получаем следующие нормальные уравнения:

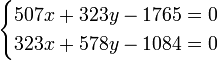
откуда x = 3,55;

y =? 0,109 Уравнения (1) представляют систему линейных уравнений, то есть уравнений, в которых все неизвестные входят в первой степени. В большинстве случаев уравнения, связывающие наблюдаемые и искомые величины, бывают высших степеней и даже трансцендентные, но это не изменяет сущности дела: предварительными изысканиями всегда можно найти величины искомых с таким приближением, что затем, разложив соответствующие функции в ряды и пренебрегая высшими степенями искомых поправок, можно привести любое уравнение к линейному.

Строгое обоснование и установление границ содержательной применимости метода даны А. А. Марковым и А. Н. Колмогоровым.

Свойства оценок на основе МНК Возможны разные виды уравнений множественной регрессии: линейные и нелинейные.

Ввиду четкой интерпретации параметров наиболее широко используется линейная функция. В линейной множественной регрессии параметры при называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

Рассмотрим линейную модель множественной регрессии. (2.1) Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака от расчетных минимальна:

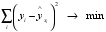
. (2.2).

Как известно из курса математического анализа, для того чтобы найти экстремум функции нескольких переменных, надо вычислить частные производные первого порядка по каждому из параметров и приравнять их к нулю.

Имеем функцию аргумента:

.

Находим частные производные первого порядка:

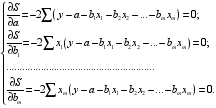
После элементарных преобразований приходим к системе линейных нормальных уравнений для нахождения параметров линейного уравнения множественной регрессии (2.1):

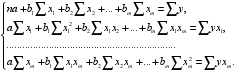
(2.3).

Для двухфакторной модели данная система будет иметь вид:

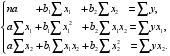
Метод наименьших квадратов применим и к уравнению множественной регрессии в стандартизированном масштабе:

(2.4).

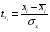
где — стандартизированные переменные:, , для которых среднее значение равно нулю:, а среднее квадратическое отклонение равно единице:; - стандартизированные коэффициенты регрессии.

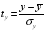
Стандартизованные коэффициенты регрессии показывают, на сколько единиц изменится в среднем результат, если соответствующий фактор изменится на одну единицу при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии можно сравнивать между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.

Применяя МНК к уравнению множественной регрессии в стандартизированном масштабе, получим систему нормальных уравнений вида.

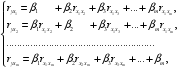
(2.5).

где и — коэффициенты парной и межфакторной корреляции.

Коэффициенты «чистой» регрессии связаны со стандартизованными коэффициентами регрессии следующим образом:

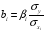
. (2.6).

Поэтому можно переходить от уравнения регрессии в стандартизованном масштабе (2.4) к уравнению регрессии в натуральном масштабе переменных (2.1), при этом параметр определяется как .

Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов — из модели исключаются факторы с наименьшим значением .

На основе линейного уравнения множественной регрессии.

(2.7).

могут быть найдены частные уравнения регрессии:

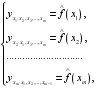
(2.8).

т.е. уравнения регрессии, которые связывают результативный признак с соответствующим фактором при закреплении остальных факторов на среднем уровне. В развернутом виде систему (2.8) можно переписать в виде:

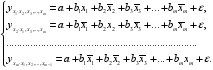
При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т. е. имеем.

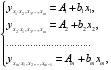
(2.9) где.

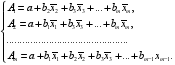
В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности:

(2.10).

где — коэффициент регрессии для фактора в уравнении множественной регрессии, — частное уравнение регрессии.

Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности:

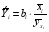
(2.11).

которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.

Парная линейная регрессия. Метод наименьших квадратов.

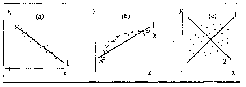
Рис. 1.

На рисунке изображены три ситуации:

на графике (а) взаимосвязь х и у близка к линейной; прямая линия (1) здесь близка к точкам наблюдений, и последние отклоняются от нее лишь в результате сравнительно небольших случайных воздействий;

на графике (b) реальная взаимосвязь величин х и у описывается нелинейной функцией (2), и какую бы мы ни провели прямую линию (например, 1), отклонения точек наблюдений от нее будут существенными и неслучайными;

на графике © явная взаимосвязь между переменными х и у отсутствует; какую бы мы ни выбрали формулу связи, результаты ее параметризации будут здесь неудачными. В частности, прямые линии 1 и 2, проведенные через «центр» «облака» точек наблюдений и имеющие противоположный наклон, одинаково плохи для того, чтобы делать выводы об ожидаемых значениях переменной у по значениям переменной х.

Начальным пунктом эконометрического анализа зависимостей обычно является оценка линейной зависимости переменных. Если имеется некоторое «облако» точек наблюдений, через него всегда можно попытаться провести такую прямую линию, которая является наилучшей в определенном смысле среди всех прямых линий, то есть «ближайшей» к точкам наблюдений по их совокупности. Для этого мы вначале должны определить понятие близости прямой к некоторому множеству точек на плоскости; меры такой близости могут быть различными. Однако любая разумная мера должна быть, очевидно, связана с расстояниями от точек наблюдений до рассматриваемой прямой линии (задаваемой уравнением у= а + bх).

Обычно в качестве критерия близости используется минимум суммы квадратов разностей наблюдений зависимой переменной у и теоретических, рассчитанных по уравнению регрессии значений (а + bхi): Q = ei2 = (yi- (a+bxi)) 2 min (1) считается, что у и х — известные данные наблюдений, а и b — неизвестные параметры линии регрессии. Поскольку функция Q непрерывна, выпукла и ограничена снизу нулем, она имеет минимум. Для соответствующих точке этого минимума значений, а и b могут быть найдены простые и удобные формулы (они будут приведены ниже). Метод оценивания параметров линейной регрессии, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от искомой линейной функции, называется Методом наименьших квадратов (МНК), или Least Squares Method (LS).

" Наилучшая" по МНК прямая линия всегда существует, но даже наилучшая не всегда является достаточно хорошей. Если в действительности зависимость y=f (х) является, например, квадратичной (как на рисунке 1 (b)), то ее не сможет адекватно описать никакая линейная функция, хотя среди всех таких функций обязательно найдется «наилучшая». Если величины х и у вообще не связаны (рис. 1 (с)), мы также всегда сможем найти «наилучшую» линейную функцию у = а+bх для данной совокупности наблюдений, но в этом случае конкретные значения, а и b определяются только случайными отклонениями переменных и сами будут очень сильно меняться для различных выборок из одной и той же генеральной совокупности. Возможно, на рис. 1 © прямая 1 является наилучшей среди всех прямых линий (в смысле минимального значения функции Q), но любая другая прямая, проходящая через центральную точку «облака» (например, линия 2), ненамного в этом смысле хуже, чем прямая 1, и может стать наилучшей в результате небольшого изменения выборки.

Рассмотрим теперь задачу оценки коэффициентов парной линейной регрессии более формально. Предположим, что связь между х и у линейна: у = +х. Здесь имеется в виду связь между всеми возможными значениями величин х и у, то есть для генеральной совокупности. Наличие случайных отклонений, вызванных воздействием на переменную у множества других, неучтенных в нашем уравнении факторов и ошибок измерения, приведет к тому, что связь наблюдаемых величин xi и yi приобретет вид уi=+хi+єi,. Здесь єi. — случайные ошибки (отклонения, возмущения). Задача состоит в следующем: по имеющимся данным наблюдений {xi}, {уi} оценить значения параметров айв, обеспечивающие минимум величины Q. Если бы были известны точные значения отклонений єi, то можно было бы (в случае правильности предполагаемой линейной формулы) рассчитать значения параметров и. Однако значения случайных отклонений в выборке неизвестны, и по наблюдениям xi и уi можно получить оценки параметров с и р, которые сами являются случайными величинами, поскольку соответствуют случайной выборке. Пусть, а — оценка параметра, b — оценка параметра. Тогда оцененное уравнение регрессии будет иметь вид:

yi=а+bxi+еi, где еi — наблюдаемые значения ошибок єi.

Для оценки параметров и воспользуемся МНК, который минимизирует сумму квадратов отклонений фактических значений уi от расчетных. Минимум ищется по переменным, а и b.

Для того, чтобы полученные МНК оценки, а и b обладали желательными свойствами, сделаем следующие предпосылки об отклонениях єi:

• 1) величина єi является случайной переменной;
• 2) математическое ожидание єi равно нулю: М (єi) = 0;
• 3) дисперсия є постоянна: D (єi) = D (єi) = 2 для всех i, j;
• 4) значения єi независимы между собой. Откуда вытекает, в частности, что (2) Известно, что, если условия 1) — 4) выполняются, то оценки, сделанные с помощью МНК, обладают следующими свойствами:
• 1) Оценки являются несмещенными, т. е. математическое ожидание оценки каждого параметра равно его истинному значению: М (а) =; М (b) =. Это вытекает из того, что М (єi) = 0, и говорит об отсутствии систематической ошибки в определении положения линии регрессии.
• 2) Оценки состоятельны, так как дисперсия оценок параметров при возрастании числа наблюдений стремится к нулю:;. Иначе говоря, если п достаточно велико, то практически наверняка, а близко к, а b близко к: надежность оценки при увеличении выборки растет.
• 3) Оценки эффективны, они имеют наименьшую дисперсию по сравнению с любыми другими оценками данного параметра, линейными относительно величин уi. В англоязычной литературе такие оценки называются BLUE (Best Linear Unbiased Estimators — наилучшие линейные несмещенные оценки).

Перечисленные свойства не зависят от конкретного вида распределения величин єi, тем не менее, обычно предполагается, что они распределены нормально N (0; y2). Эта предпосылка необходима для проверки статистической значимости сделанных оценок и определения для них доверительных интервалов. При ее выполнении оценки МНК имеют наименьшую дисперсию не только среди линейных, но среди всех несмещенных оценок.

Если предположения 3) и 4) нарушены, то есть дисперсия возмущений непостоянна и/или значения є. связаны друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности — нет.

Рассмотрим теперь процедуру оценивания параметров парной линейной регрессии, а и b. Для того, чтобы функция Q = ei2 = (yi- (a+bxi)) 2достигала минимума, необходимо равенство нулю ее частных производных:

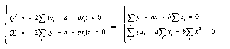
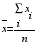
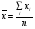
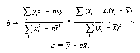
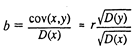
(3) (4) Если уравнение (3) разделить на n, то получим у=а+bх (здесь — средние значения х и у). Таким образом, линия регрессии проходит через точку со средними значениями х и у. Подставив величину, а из (3) в (4), получаем Откуда (5) (6) Иначе можно записать, что (где r коэффициент корреляции х и у). Таким образом, коэффициент регрессии пропорционален показателю ковариации и коэффициенту корреляции х и у, а коэффициенты этой пропорциональности служат для соизмерения перечисленных разноразмерных величин. Оценки a и b, очевидно, являются линейными относительно yi (если xi считать коэффициентами) — выше об этом упоминалось.

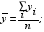
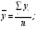
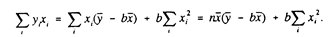
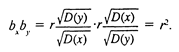
Итак, если коэффициент r уже рассчитан, то легко рассчитать коэффициент парной регрессии, не решая системы уравнений. Ясно также, что если рассчитаны линейные регрессии х (у) и у (х), то произведение коэффициентов dx и by, равно r2: (7) [1] Взвешенный метод наименьших квадратов Далеко не все задачи исследования взаимосвязей экономических переменных описываются обычной линейной регрессионной моделью. Во-первых, исходные данные могут не соответствовать тем или иным предпосылкам линейной регрессионной модели и требовать либо дополнительной обработки, либо иного модельного инструментария. Во-вторых, исследуемый процесс во многих случаях описывается не одним уравнением, а системой, где одни и те же переменные могут быть в одних случаях объясняющими, а в других — зависимыми. В-третьих, исследуемые взаимосвязи могут быть (и обычно являются) нелинейными, а процедура линеаризации не всегда легко осуществима и может приводить к искажениям. В-четвертых, структура описываемого процесса может обусловливать наличие различного рода связей между оцениваемыми коэффициентами регрессии, что также предполагает необходимость использования специальных методов.

Наиболее распространенным в практике статистического оценивания параметров уравнений регрессии является метод наименьших квадратов. Этот метод основан на ряде предпосылок относительно природы данных и результатов построения модели. Основные из них — это четкое разделение исходных переменных на зависимые и независимые, некоррелированность факторов, входящих в уравнения, линейность связи, отсутствие автокорреляции остатков, равенство их математических ожиданий нулю и постоянная дисперсия. Эмпирические данные не всегда обладают такими характеристиками, т. е. предпосылки МНК нарушаются. Применение этого метода в чистом виде может привести к таким нежелательным результатам, как смещение оцениваемых параметров, снижение их состоятельности, устойчивости, а в некоторых случаях может и вовсе не дать решения. Для смягчения нежелательных эффектов при построении регрессионных уравнений, повышения адекватности моделей существует ряд усовершенствований МНК, которые применяются для данных нестандартной природы.

Одной из основных гипотез МНК является предположение о равенстве дисперсий отклонений еi, т. е. их разброс вокруг среднего (нулевого) значения ряда должен быть величиной стабильной. Это свойство называется гомоскедастичностью. На практике дисперсии отклонений достаточно часто неодинаковы, то есть наблюдается гетероскедастичность. Это может быть следствием разных причин. Например, возможны ошибки в исходных данных. Случайные неточности в исходной информации, такие как ошибки в порядке чисел, могут оказать ощутимое влияние на результаты. Часто больший разброс отклонений єi, наблюдается при больших значениях зависимой переменной (переменных). Если в данных содержится значительная ошибка, то, естественно, большим будет и отклонение модельного значения, рассчитанного по ошибочным данным. Для того, чтобы избавиться от этой ошибки нам нужно уменьшить вклад этих данных в результаты расчетов, задать для них меньший вес, чем для всех остальных. Эта идея реализована во взвешенном МНК.

Пусть на первом этапе оценена линейная регрессионная модель с помощью обычного МНК. Предположим, что остатки еi независимы между собой, но имеют разные дисперсии (поскольку теоретические отклонения еi нельзя рассчитать, их обычно заменяют на фактические отклонения зависимой переменной от линии регрессии, для которых формулируются те же исходные требования, что и для єi). В этом случае квадратную матрицу ковариаций cov (ei, ej) можно представить в виде:

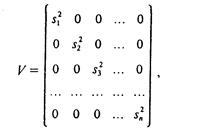
где cov (ei, ej) =0 при i j; cov (ei, ej) =S2; n — длина рассматриваемого временного ряда.

Если величины известны, то далее можно применить взвешенный МНК, используя в качестве весов величины и минимизируя сумму.

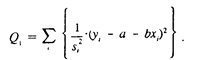
Формула Q, записана для парной регрессии; аналогичный вид она имеет и для множественной линейной регрессии. При использовании IVLS оценки параметров не только получаются несмещенными (они будут таковыми и для обычного МНК), но и более точными (имеют меньшую дисперсию), чем не взвешенные оценки.

Проблема заключается в том, чтобы оценить величины s2, поскольку заранее они обычно неизвестны. Поэтому, используя на первом этапе обычный МНК, нужно попробовать выяснить причину и характер различий дисперсий еi. Для экономических данных, например, величина средней ошибки может быть пропорциональна абсолютному значению независимой переменной. Это можно проверить статистически и включить в расчет МНК веса, равные .

Существуют специальные критерии и процедуры проверки равенства дисперсий отклонений. Например, можно рассмотреть частное от деления cумм самых больших и самых маленьких квадратов отклонений, которое должно иметь распределение Фишера в случае гомоскедастичности.

Использование взвешенного метода в статистических пакетах, где предоставлена возможность задавать веса вручную, позволяет регулировать вклад тех или иных данных в результаты построения моделей. Это необходимо в тех случаях, когда мы априорно знаем о не типичности какой-то части информации, т. е. на зависимую переменную оказывали влияние факторы, заведомо не включаемые в модель. В качестве примера такой ситуации можно привести случаи стихийных бедствий, засух. При анализе макроэкономических показателей (ВНП и др.) данные за эти годы будут не совсем типичными. В такой ситуации нужно попытаться исключить влияние этой части информации заданием весов. В разных статистических пакетах приводится возможный набор весов. Обычно это числа от О до 100. По умолчанию все данные учитываются с единичными весами. При указании веса меньше 1 мы снижаем вклад этих данных, а если задать вес больше единицы, то вклад этой части информации увеличится. Путем задания весового вектора мы можем не только уменьшить влияние каких — либо лет из набора данных, но и вовсе исключить его из анализа. Итак, ключевым моментом при применении этого метода является выбор весов. В первом приближении веса могут устанавливаться пропорционально ошибкам не взвешенной регрессии. [1] Системы одновременных уравнений При статистическом моделировании экономических ситуаций часто необходимо построение систем уравнений, когда одни и те же переменные в различных регрессионных уравнениях могут одновременно выступать, с одной стороны, в роли результирующих, объясняемых переменных, а с другой стороны — в роли объясняющих переменных. Такие системы уравнений принято называть системами одновременных уравнений. При этом в соотношения могут входить переменные, относящиеся не только к текущему периоду t, но и к предшествующим периодам. Такие переменные называются лаговыми. Переменные за предшествующие годы обычно выступают в качестве объясняющих переменных.

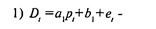
В качестве иллюстрации приведем пример из экономики. Рассмотрим модель спроса и предложения. Как известно, спрос D на некоторый продукт зависит от его цены р. От этого же параметра, но с противоположным по знаку коэффициентом, зависит и предложение этого продукта. Силы рыночного механизма формируют цену таким образом, что спрос и предложение уравниваются. Нам нужно построить модель описанной ситуации. Для этого имеются данные об уровне равновесных цен и спросе (который равен предложению). Представленную ситуацию можно формализовать в виде следующей линейной модели: (3.1) спрос пропорционален цене с коэффициентом пропорциональности a10, т. е. связь положительная; (3.3) Здесь еl, е’l, (l=1,., n) — ошибки модели, имеющие нулевое математическое ожидание.

Первые два из представленных уравнений, если их рассматривать отдельно, могут показаться вполне обычными. Мы можем определить коэффициенты регрессии для каждого из этих уравнений. Но в этом случае остается открытым вопрос о равенстве спроса и предложения, т. е. может не выполняться третье равенство, в котором спрос выступает в качестве зависимой переменной. Поэтому расчет параметров отдельных уравнений в такой ситуации теряет смысл.

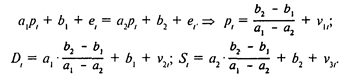
Экономическая модель как система одновременных уравнений может быть представлена в структурной или в приведенной форме. В структурной форме ее уравнения имеют исходный вид, отражая непосредственные связи между переменными. Приведенная форма получается после решения модели относительно эндогенных (внутренних) переменных, то есть выражения этих переменных только через экзогенные (задаваемые извне) переменные и параметры модели. Например, в модели спроса и предложения эндогенными являются переменные pl, Sl, Dl, ее параметры — a1, a2, b1, b2, а экзогенных переменных в ней нет. Таким образом, в приведенной форме переменные pl, Sl, Dl, должны выражаться только через параметры модели. Подставив Sl и Dl из (1) и (2) в (3), получаем Здесь v1l, v2l, v3l — преобразованные отклонения. Мы можем оценить как среднее значение pl (т.е.), а также, , но из этих трех соотношений невозможно рассчитать параметры первоначальной модели a1, a2, b1 и b2 (поскольку их четыре). Тем самым мы подошли к проблеме идентификации — оценке параметров структурной формы модели (в чем, собственно, и состоит наша задача) по параметрам приведенной формы. Параметры приведенной формы могут быть оценены обычным МНК, но по ним далеко не всегда может быть идентифицирована исходная модель (как, например, в описанном случае модели спроса и предложения). Для того чтобы структурная форма модели могла быть идентифицирована, вводят дополнительные предпосылки (например, о равенстве некоторых коэффициентов нулю или об их взаимосвязи между собой). Часто уже на этапе построения модели стараются выбрать такую ее форму, которая была бы идентифицируема. Такой, например, является треугольная форма модели: (3.4) где х — вектор объясняющих переменных, yi — зависимая переменная. Нежелательна и сверхидентифицируемость модели, когда для параметров структурной формы получается слишком много со отношений из приведенной формы модели. В этом случае модель также нуждается в уточнении.

Для оценивания систем одновременных уравнений имеется ряд методов. В целом их можно разбить на две группы. К первой группе относятся методы, применяемые к каждому уравнению в отдельности. Вторая группа содержит методы, предназначенные для оценивания всей системы в целом. В пакете TSP, в частности, представлено по одному методу из каждой группы. Для оценивания отдельных уравнений можно применять двухшаговый метод наименьших квадратов (Two-Stage Least Squares). Из второй группы методов в этом пакете реализован трехшаговый метод наименьших квадратов (Three-Stage Least Squares), Остановимся вначале на двухшаговом методе. Он применяется при наличии в оцениваемой модели лаговых переменных.

Содержательный смысл двухшагового метода состоит в следующем. Как известно, МНК-оценки параметров уравнения равны b= (Х'Х) — 1 X’Y, но лаговые значения у, используемые как объясняющие переменные (в этой формуле они являются частью матрицы X), заранее неизвестны. Поэтому для того, чтобы воспользоваться этой формулой, сначала, на первом шаге, определяются недостающие значения объясняемых переменных. Это в данном случае делается путем расчета МНК-оценок, т. е. строится регрессия, в которой в роли объясняемых переменных выступают только имеющиеся в исходной информации. После этого, когда исходные эмпирические данные дополнены рассчитанными значениями и сформирован полный набор данных, можно приступать к оценке искомых параметров.

Двухшаговый МНК применяется и при сверхидентифицируемости модели. В этом случае на первом шаге оцениваются параметры приведенной формы модели. С помощью уравнений приведенной формы, при заданных значениях объясняющих переменных, рассчитываются оценки зависимых переменных. Далее эти оценки подставляются в правые части уравнений модели в структурной форме, и вновь используется обычный МНК для оценки ее параметров.

Для оценки параметров всей системы уравнений в целом используется трехшаговый МНК. К его применению прибегают в тех случаях, когда переменные, объясняемые водном уравнении, в другом выступают в роли объясняющих. Так было в нашем примере с моделью спроса и предложения, где спрос и предложение, с одной стороны, определяются рыночной ценой, а с другой стороны, предложение должно быть равно спросу. При расчете параметров таких моделей необходимо учитывать всю систему соотношений. В трехшаговом методе это реализуется в три этапа. Первые два из них похожи на двухшаговый метод, т. е. производится оценка параметров в уравнениях с лаговыми переменными. В нашем примере лаговые переменные в уравнения не включены, и на этом этапе будут рассчитываться обычные коэффициенты регрессии. После этого нам нужно увязать все уравнения системы между собой. В качестве меры связи здесь выступает матрица ковариаций ошибок моделей, т. е. чтобы оценить, насколько несвязанными получатся уравнения спроса и предложения при расчете их отдельно, нужно рассчитать ковариацию ошибок е и е'. Для увеличения этой связи на следующем этапе, при очередном расчете коэффициентов регрессии учитывается матрица ковариаций ошибок. Таким приемом достигается взаимосязанность всей системы уравнений. [1].

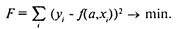
Нелинейная регрессия На практике часто встречается ситуация, когда априорно известен нелинейный характер зависимости между объясняемыми и объясняющими переменными. В этом случае функция f в уравнении у= (а, х) нелинейна (а — вектор параметров функции, которые нам нужно оценить). Например, вид зависимости между ценой и количеством товара в той же модели спроса и предложения: она не всегда предполагается линейной, как в нашем примере. Нелинейную функцию можно преобразовать в линейную, как это было сделано, например, логарифмированием с функцией Кобба-Дугласа. Однако не все функции поддаются такой непосредственной линеаризации. Любую дифференцируемую нужное число раз функцию можно разложить в функциональный ряд и затем оценить регрессию объясняемой переменной с членами этого ряда. Тем не менее такое разложение всегда осуществляется в окрестности определенной точки, и лишь в этой окрестности достаточно точно аппроксимирует оцениваемую функцию. В то же время оценить зависимость требуется обычно на более или менее значительном интервале, а не только в окрестности некоторой точки. При линеаризации функции или разложении её в ряд с целью оценки регрессии возникают и другие проблемы: искажение отклонений ей нарушение их первоначальных свойств, статистическая зависимость членов ряда между собой. Например, если оценивается формула полученная путем линеаризации или разложения в ряд, то независимые переменные х и х2 связаны между собой даже не статистически, но функционально. Если исходная ошибка е здесь связана с переменной х, то добавление х2 приводит к появлению (с соответствующими коэффициентами) квадрата этой переменной и её удвоенного произведения с х, что искажает исходные предпосылки модели. Поэтому во многих случаях актуальна непосредственная оценка нелинейной формулы регрессии. Для этого можно воспользоваться нелинейным МНК. Идея МНК основана на том, чтобы минимизировать сумму квадратов отклонений расчетных значений от эмпирических, т. е. нужно оценить параметры о функции f (a, x) таким образом, чтобы ошибки еi= уi-f (а, х), точнее — их квадраты, по совокупности были минимальными. Для этого нужно решить задачу минимизации (4.1) Для решения этой задачи существует два пути. Во-первых, может быть осуществлена непосредственная минимизация функции F с помощью методов нелинейной оптимизации, позволяющих находить экстремумы выпуклых линий. Это, например, метод наискорейшего спуска, при использовании которого в некоторой исходной точке определяется антиградиент (направление наиболее быстрого убывания) функции F. Далее находится минимум F при движении в данном направлении, и в точке этого минимума снова определяется градиент. Процедура повторяется до тех пор, пока разница значений f на двух последовательных шагах не окажется меньше заданной малой величины. Другой путь состоит в решении системы нелинейных уравнений, которая получается из необходимых условий экстремума функции F. Эти условия — равенство нулю частных производных функции F по каждому из параметров аj., т. е.

Faj = 0, j =1,., m. Получается система уравнений -2 (yi-f (a, xi)) *fai' (a, xi) = 0, j = 1,., m (4.2) нелинейность которой обусловлена нелинейностью функции f относительно параметров аj. Эта система уравнений может быть решена итерационными методами (когда последовательно находятся векторы параметров, все в меньшей степени нарушающие уравнения системы). Однако в общем случае решение такой системы не является более простым способом нахождения вектора а, чем непосредственная оптимизация методом наискорейшего спуска.

Существуют методы оценивания нелинейной регрессии, сочетающие непосредственную оптимизацию, использующую нахождение градиента, с разложением в функциональный ряд (ряд Тейлора) для последующей оценки линейной регрессии. Наиболее известен из них метод Марквардта, сочетающий в себе достоинства каждого из двух используемых методов.

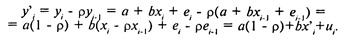
При построении нелинейных уравнений более остро, чем в линейном случае, стоит проблема правильной оценки формы зависимости между переменными. Неточности при выборе формы оцениваемой функции существенно сказываются на качестве отдельных параметров уравнений регрессии и, соответственно, на адекватности всей модели в целом. [1] Авторегрессионное преобразование Важной проблемой при оценивании регрессии является автокорреляция остатков е, которая говорит об отсутствии первоначально предполагавшейся их взаимной независимости. Автокорреляция остатков первого порядка, выявляемая с помощью статистики Дарбина-Уотсона, говорит о неверной спецификации уравнения либо о наличии неучтенных факторов. Естественно, для её устранения нужно попытаться выбрать более адекватную формулу зависимости, отыскать и включить важные неучтенные факторы или уточнить период оценивания регрессии. В некоторых случаях, однако, это не даст результата, а отклонения еi просто связаны авторегрессионной зависимостью. Если это авторегрессия первого порядка, то её формула имеет вид еi=ei-1 + ui (- коэффициент авторегрессии, ||<1), и мы предполагаем, что остатки ui в этой формуле обладают нужными свойствами, в частности — взаимно независимы. Оценив, введем новые переменные у’i=уi — yi-1; x’i=xi — xi-1;^,. (это преобразование называется авторегрессионным (AR), или преобразованием Бокса-Дженкинса). Пусть мы оцениваем первоначально формулу линейной регрессии уi= а + bxi + еi. Тогда Если величины ui. действительно обладают нужными свойствами, то в линейной регрессионной зависимости у’i= а1 + bx’i + ui автокорреляции остатков ui уже не будет, и статистика DW окажется близкой к двум. Коэффициент b этой формулы принимается для исходной формулы у = а+bх+е непосредственно, а коэффициент а, рассчитывается по формуле .

Оценки коэффициентов, а и b нужно сравнить с первоначальными оценками, полученными для расчета отклонений еi Если эти оценки совпадают, то процесс заканчивается; если нет — то при новых значениях, а и b вновь рассчитываются отклонения е до тех пор, пока оценки, а и b на двух соседних итерациях не совпадут с требуемой точностью.

В случае, когда остатки «также автокоррелированы, авторегрессионное преобразование может быть применено ещё раз. Это означает использование авторегрессионного преобразования более высокого порядка, которое заключается в оценке коэффициентов авторегрессии соответствующего порядка для отклонений е. и использовании их для построения новых переменных. Такое преобразование вместо AR (1) называется AR (s) — если используется авторегрессия порядка s.

О целесообразности применения авторегрессионного преобразования говорит некоррелированность полученных отклонений ui,. Однако даже в этом случае истинной причиной первоначальной автокорреляции остатков может быть нелинейность формулы или неучтенный фактор. Мы же, вместо поиска этой причины, ликвидируем её бросающееся в глаза следствие. В этом — основной недостаток метода AR и содержательное ограничение для его применения.

Кроме авторегрессионного преобразования, для устранения автокорреляции остатков и уточнения формулы регрессионной зависимости может использоваться метод скользящих средних (MovingAve-rages, или МА). В этом случае считается, что отклонения от линии регрессии еi описываются как скользящие средние случайных нормально распределенных ошибок еi предполагается, что (5.1) Это формула для преобразования МА q-го порядка, или MA (q); МА (1), например, имеет вид еi = єi + iєi-1. Параметры i, как и в случае авторегрессионного преобразования, могут оцениваться итерационными методами.

Во многих случаях сочетание методов AR и МА позволяет решить проблему автокорреляции остатков даже при небольших s и q. Еще раз повторим, что адекватным такое решение проблемы является лишь в том случае, если автокорреляция остатков имеет собственные внутренние причины, а не вызвана наличием неучтенных (одного или нескольких) факторов.

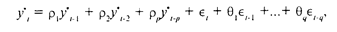
Методы AR и МА могут использоваться в сочетании с переходом от объемных величин в модели к приростным, для которых статистическая взаимосвязь может быть более точной и явной. Модель, сочетающая все эти подходы, называется моделью ARIMA (Autoregressive Integrated Moving Averages). В общем виде ее формулу можно записать так: (5.2) где {р^} и {9^} - неизвестные параметры, и е — независимые, одинаково нормально распределенные СВ с нулевым средним. Величины у* представляют собой конечные разности порядка d величин у, а модель обозначается как АRIМА (р, d, q).

Применение МНК в экономике Порядок применения шкалы регрессии ставок единого социального налога налогоплательщиками, указанными в подпункте 1 пункта 1 статьи 235 Налогового кодекса Российской Федерации (т.е. налогоплательщиками-работодателями, включая работодателей-предпринимателей без образования юридического лица).

В соответствии с пунктом 2 статьи 241 и статьи 245 Налогового кодекса Российской Федерации шкала регрессии ставок единого социального налога в 2001 г. применяется налогоплательщиками при условии, что фактический размер выплат, начисленный в среднем на одного работника и принимавшийся за базу при расчете страховых взносов в Пенсионный фонд Российской Федерации во втором полугодии 2000 г., превышал 25 000 рублей.

При этом у налогоплательщиков с численностью работников свыше 30 человек не учитываются выплаты 10 процентам работников, имеющих наибольшие по размеру выплаты, у налогоплательщиков с численностью работников до 30 человек (включительно) — выплаты 30 процентам работников, имеющих наибольшие по размеру выплаты.

Широкое применение линейной регрессии обусловлено тем, что достаточно большое количество реальных процессов в экономике и бизнесе можно с достаточной точностью описать линейными моделями. В Data Mining, регрессия широко используется для решения задачпрогнозирования и численного предсказания.

Заключение

Информация, представленная в настоящем реферате, может стать основой для дальнейшей проработки и усовершенствования приведенных статистических методов. По каждому из описанных методов может быть предложена задача построения соответствующих алгоритмов. По разработанным алгоритмам в дальнейшем возможна разработка программных продуктов для практического использования методов в аналитических, исследовательских, коммерческих и других областях.

Наиболее полная информация приведена по применению скользящих средних. В работе описывается лишь малая часть имеющихся в настоящее время методов для исследования и обработки различных видов статистической информации. Здесь представлен краткий и поверхностный обзор некоторых методов, исходя из незначительного объёма настоящей работы.

• 1. О. О. Замков, А. В. Толстопятенко, Р. Н. Черемных Взвешенный метод наименьших квадратов Взвешенный метод наименьших квадратов Математические методы в экономике. — М.: Дис, 1997.
• 2. Анна Эрлих Технический анализ товарных и финансовых рынков. — М.: ИНФРА, 1996.
• 3. Я. Б. Шор Статистические методы анализа и контроля качества и надёжности. — М.: Советское радио, 1962.
• 4. В. С. Пугачёв Теория вероятностей и математическая статистика. — М.: Наука, 1979. — 394 с.
• 5. Стренг Г. Линейная алгебра и ее применения. М.: Мир. 1980.
• 6. Каханер Д., Моулер К., Нэш С. Численные методы и программное обеспечение. М.: Мир. 1998.
• 7. Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008.55 с. Брошюра, PDF.