Вопросы и задания для повторения

• 1. Что называется пространством элементарных исходов?
• 2. Какие события называются случайными, несовместными?
• 3. Что называется вероятностью события? Каковы ее свойства?
• 4. Что называется вероятностным пространством?
• 5. Что называется статистической устойчивостью частот?
• 6. Привести условия реализации формулы классической вероятности.
• 7. Что такое геометрическая вероятность?
• 8. Какие события называются независимыми?
• 9. Что называется условной вероятностью?
• 10. Сформулировать и доказать теорему умножения вероятностей. Привести следствия теоремы.
• 11. Вывести формулу полной вероятности.
• 12. Вывести формулу Байеса.

Примеры решения задач

Задача 2.1. На юбилей фирмы каждому из 30 сотрудников давался номерной пригласительный билет в ресторан. Среди других мероприятий были разыграны 15 призов по случайно выбранным номерам. Какова вероятность того, что среди 15 сотрудников, оказавшихся за одним столом, восемь человек получили призы?

Решение. Из 30 билетов одновременно выбирается 15 шт., порядок выбора не существен. Пространство элементарных исходов есть число сочетаний из 30 по 15: С^. Среди 15 призеров за первым столом оказались 8 человек. Число способов выбора равно Cf₅. Оставшиеся 7 человек за столом не получили призы. Это величина С^₅. Возможен другой вариант, когда за вторым столом оказалось 8 призеров. Вероятность того, что за одним из двух столов сидели 8 призеров, равна

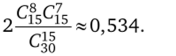
Задача 2.2. Найти вероятность того, что в семизначном номере присутствуют всего три различные цифры, причем две из них встречаются трижды.

Решение. Пространство элементарных исходов содержит события, число которых есть число размещений с повторениями, равное 10⁷. Выбираем одну из 10 цифр (всего 10 вариантов) и ставим на три места семизначного номера (всего С| способов). Затем из оставшихся 9 цифр выбираем также одну (9 вариантов) и заполняем ею три места из оставшихся (всего С| способов). Наконец из 8 цифр выбираем одну (всего 8 вариантов) и размещаем ее на единственном оставшемся месте (1 вариант). Вероятность события.

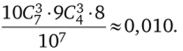
Задача 2.3. Одновременно бросаются пять игральных кубиков. Найти вероятность того, хотя бы на одном из них выпадет шестерка.

Решение. Задача может быть решена при суммировании вероятностей случаев выпадения шестерки один раз, два раза и т. д. Тем не менее задачи, в которых встречается сочетание «хотя бы один раз», удобно решать методом от противного. Вероятность того, что шестерка не выпадет при одном бросании кубика, равна —. Вероятность того, что.

шестерка не выпадет на пяти кубиках, равна. Тогда вероятность.

( 5^.

выпадения шестерки хотя бы один раз будет равна 1−1 — 1 * 0,598.

Задача 2.4. Наудачу взяты два натуральных числа х и у, каждое из которых не превышает десяти. Найти вероятность того, что их сумма окажется не более 12.

Решение. Пространство элементарных исходов содержит события, число которых равно 10 • 10 = 100. Возьмем первое число равным единице. Тогда второе может быть любым от 1 до 10, всего 10 случаев. Если первое число равно 2, то второе также может быть любым от 1 до 10. Если первое число равно 3, то второе может меняться от 1 до 9. Перебирая таким образом значения первого числа от 1 до 10, получим количество случаев 10 + 10 + 9 + 8 + 7−1-6−1-5−1-4−1-3 + 2 = 64. Вероятность того, что их сумма окажется не более 12, равна 64/100 = 0,64.

Задача 2.5. Эксперт принимает правильное решение с вероятностью р >—. Чтобы увеличить число верных решений, была создана группа для принятия решений в составе трех человек, два из которых — известные эксперты, компетентность третьего неизвестна. Как будет меняться доля правильных решений группы по сравнению с решением, принимаемым одним экспертом, в зависимости от компетентности третьего члена комиссии?

Решение. Пусть вероятность принятия правильного решения независимыми экспертами, А и В равна р, третьим членом группы С — х. Правильное решение принимается группой в составе трех человек большинством голосов с вероятностью.

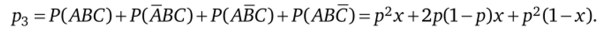
Сравним работу группы с работой одного эксперта. Предположим, что доля правильных решений группы выше. Тогда.

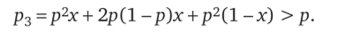
После преобразований получим р₃ — р = (1 — р) р (2х — 1) > 0.

1. Если вероятность х принятия правильного решения третьим членом группы больше —, то число правильных решений при этом повышается по сравнению с работой одного эксперта. Пусть х = р. Процент верных решений повысится на величину.

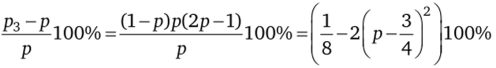
и может достичь величины 12,5% (процент повышения правильных решений группой экспертов по сравнению с одним экспертом).

2. Если третий член группы экспертов некомпетентен, принимая решения случайным образом «чет-нечет» (х = —), то р₃ = р. Некомпетентный член группы как бы нейтрализует работу одного из двух экспертов.

3. Наконец, если третий член группы, имея искаженные знания о предмете, чаще принимает неверные решения (х<�Д), то работа экспертной группы фактически блокируется: р₃ < р.

Задача 2.6. На окружности радиусом R наудачу проводится хорда, параллельная данному направлению. Какова вероятность того, что длина хорды не превысит Я?

Решение. Совместим центр окружности с началом декартовой системы координат. Из геометрических соображений находим длину хорды: l = 2IR^[1] -х^[1], где х — расстояние от начала координат до хорды. Поскольку она должна быть не больше радиуса, то, решая неравенство.

• 2IR^[1]-x^[1] получаем |х|>^-Р. Событию l благоприятствует мно-
• 7з 7з

жество значений х е -R;——R u -^-R;R из промежутка х е [-Я;Р]. Вероятность этого события равна.

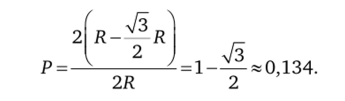
Задача 2.7. Рабочий, имея в ящике 10 деталей, среди которых четыре бракованные, должен вынуть стандартную. Какова вероятность, что ею окажется четвертая деталь, вынутая из ящика?

Решение. Если только четвертая деталь оказалась стандартной, то первые три были бракованные. Рабочий вынимает первую бракован;

ную деталь с вероятностью — (исход Л), вторую бракованную деталь —.

с вероятностью — (исход В), третью бракованную деталь — с вероятноРешение, а) Известно, что ребята сели в разные автобусы. Пространство элементарных исходов будет равно А| (событие А). Число случаев, благоприятствующих событию В (кто-то сел в первый автобус) при упорядоченном выборе равно А. Второй попал либо во второй, либо в третий автобус. Всего два случая. Тогда вероятность Р (В |А) того, что один из них сядет в первый автобус, если известно, что они сели в разные, имеет вид.

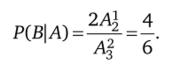
б) В отличие от первого вопроса при ответе на второй надо учитывать, что, хотя они могли расположиться в автобусах произвольным образом, случайно произошли два события: событие, А — ребята оказались в разных автобусах, событие В — кто-то из них попал в первый. В этом случае пространство элементарных исходов равно А| =3². Веро;

А² 3! 6.

ятность ребятам оказаться в разных автобусах равна Р (А)=-=^=-ф=—.

Вероятность события, что они сели в разные автобусы, причем кто-то из них оказался в первом, равна.

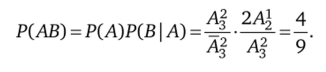
Для наглядности составим пространство элементарных событий в виде таблицы, обозначив ребят как П и В:

Таблица подтверждает, что в четырех случаях из девяти в первом вагоне находится один пассажир.

Задача 2.9. Составляются номера с пятью цифрами. При условии, что все цифры в номере разные, найти вероятность того, что среди них имеется цифра 0. Найти вероятность того, что в номере с пятью разными цифрами имеется цифра 0.

Решение. Если дано, что в номере цифры разные, пространство элементарных исходов равно Af₀ (событие А). Число случаев, благоприятствующих событию В (выбираем цифру 0) равно 1. На остальные места следует выбрать в произвольном порядке три из оставшихся девяти цифр — число способов С^. Все пять выбранных цифр следует расставить по разрядам пятизначного номера числом способов 5!, тогда номера будут разными. Вероятность Р (В |А) того, что в пятизначном числе с разными цифрами есть цифра 0, имеет вид.

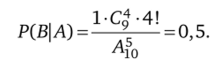
Ответ можно получить сразу. Нужно выбрать пять цифр с нулем. Остаются невыбранными также пять цифр. Результат: Р (В | А) = 0,5.

Во втором случае необходимо найти вероятность совместных событий Р (АВ): событие, А — все цифры разные, событие В — в номере есть цифра 0. Пространство элементарных исходов равно Af₀ = 10⁵. Вероятность иметь номер с различными цифрами, среди которых есть цифра 0, равна.

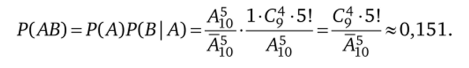
Задача 2.10. При массовом рентгеновском обследовании населения вероятность обнаружить заболевание туберкулезом у больного туберкулезом равна 0,9, вероятность принять здорового человека за больного равна 0,01. Доля больных туберкулезом по отношению ко всему населению равна 0,001. Найти вероятность того, что человек здоров, если при обследовании он был признан больным.

Решение. Введем события: пациент болен — Н_ь пациент здоров — Я₂. Вероятность того, что на обследование поступил больной пациент, Р (ЯД, здоровый — Р (Я₂).

Пусть событие, А — «пациент признан больным». Тогда событие, А — пациент признан здоровым. Сформулируем условные вероятности. По результатам обследования признанный больным пациент действительно оказался больным — Р (А|Н₁), признанный здоровым оказался больным — Р (А|Я_а), признанный больным на самом деле здоров — Р (А | Я₂), признанный здоровым действительно здоров — Р (А | Я₂). Соответствующее дерево вероятностей представлено на рис. 2.5. Вычислим сначала полную вероятность признания пациента больным:

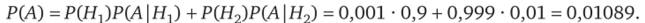
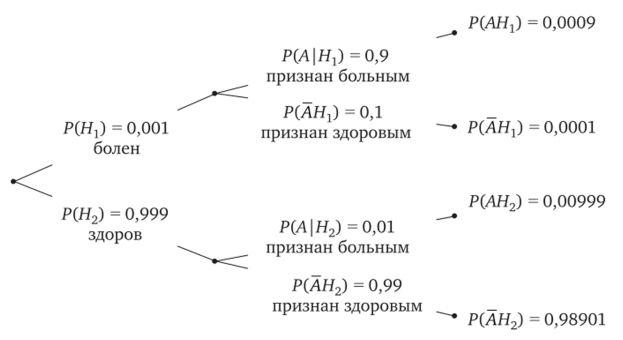
Рис. 2.5. К задаче 2.10.

Теперь вероятность того, что здорового пациента при обследовании признали больным, равна.

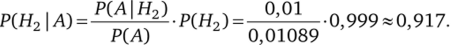
Таким образом, 91,7% людей, у которых обследование показало результат «болен», на самом деле здоровые люди. Удивительный результат возникает по причине значительной разницы в долях больных туберкулезом и здоровых. При возникновении такого результата следует сделать повторное обследование.

• [1] стью — (исход С). Наконец, ему попадается стандартная деталь, 8 вероятность вынуть которую — (исход D). По теореме умножения вероятность события, заключающегося в том, что мастер вынимает последовательно три бракованные детали и, затем стандартную, равна Задача 2.8. В молодежном лагере организована экскурсия. Подошлитри автобуса. Два приятеля Петя и Вася, потеряв друг друга в толпе, садятся в автобусы случайным образом. а) Какова вероятность Р (В |А) того, что один из них сядет в первыйавтобус, если известно, что они сели в разные автобусы? б) Найти вероятность Р (АВ) того, что хотя они попали в разные автобусы, кто-то из них оказался в первом.
• [2] стью — (исход С). Наконец, ему попадается стандартная деталь, 8 вероятность вынуть которую — (исход D). По теореме умножения вероятность события, заключающегося в том, что мастер вынимает последовательно три бракованные детали и, затем стандартную, равна Задача 2.8. В молодежном лагере организована экскурсия. Подошлитри автобуса. Два приятеля Петя и Вася, потеряв друг друга в толпе, садятся в автобусы случайным образом. а) Какова вероятность Р (В |А) того, что один из них сядет в первыйавтобус, если известно, что они сели в разные автобусы? б) Найти вероятность Р (АВ) того, что хотя они попали в разные автобусы, кто-то из них оказался в первом.
• [3] стью — (исход С). Наконец, ему попадается стандартная деталь, 8 вероятность вынуть которую — (исход D). По теореме умножения вероятность события, заключающегося в том, что мастер вынимает последовательно три бракованные детали и, затем стандартную, равна Задача 2.8. В молодежном лагере организована экскурсия. Подошлитри автобуса. Два приятеля Петя и Вася, потеряв друг друга в толпе, садятся в автобусы случайным образом. а) Какова вероятность Р (В |А) того, что один из них сядет в первыйавтобус, если известно, что они сели в разные автобусы? б) Найти вероятность Р (АВ) того, что хотя они попали в разные автобусы, кто-то из них оказался в первом.
• [4] стью — (исход С). Наконец, ему попадается стандартная деталь, 8 вероятность вынуть которую — (исход D). По теореме умножения вероятность события, заключающегося в том, что мастер вынимает последовательно три бракованные детали и, затем стандартную, равна Задача 2.8. В молодежном лагере организована экскурсия. Подошлитри автобуса. Два приятеля Петя и Вася, потеряв друг друга в толпе, садятся в автобусы случайным образом. а) Какова вероятность Р (В |А) того, что один из них сядет в первыйавтобус, если известно, что они сели в разные автобусы? б) Найти вероятность Р (АВ) того, что хотя они попали в разные автобусы, кто-то из них оказался в первом.