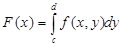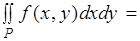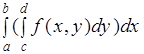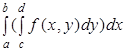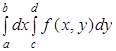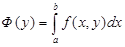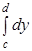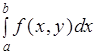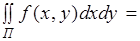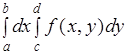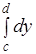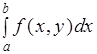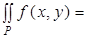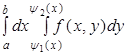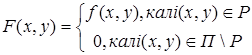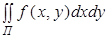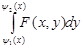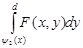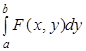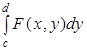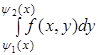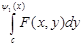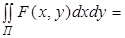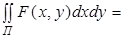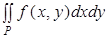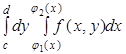Вычисление двойных интегралов

Вычисление двойного интеграла на прямоугольнике.

Теорема 1. Пусть функция f (х, у) есть интегрируемая на прямоугольнике П= и для каждого х существует интеграл Римона.

. (1).

Тогда функция интегрируема на отрезке и имеет место равенство:

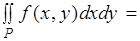
(2).

Интеграл называюць повторным интегралом и записвают его в виде: .

Замечание 1. Если х и у поменять ролями, т. е. допустить существование интеграла для каждого у, то вместо формулы (2) получаем формулу:

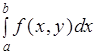
(3).

Следствие 1. Если функция f (х, у) непрерывная в прямоугольнике П=, то имеет место формула:

= (4).

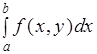
Вычисление двойного интеграла по элементарной фигуре.

Если каждая прямая, параллельная оси 0у (0х), проходящая через внутреннюю точку области Р, пересекает её границу только в двух точках, то область Р называется элементарной в отношении оси 0у (0х) или вобластью первого типа (второго типа). Таким образом:

• а) область первого типа есть фигура в плоскости х0у, которая задаётся следующим образом:, где и непрерывныя на функции;
• б) область второго типа есть фигура в плоскости х0у, которая задаётся следующим образом:, где и — непрерывные на функции.

Теорема 2. Пусть функция f (х, у) есть интегрируемая на области первого типа и для каждого х существует интеграл. Тогда справедлива формула:

. (5).

Возьмем прямоугольник П=, такой, что РП. Рассмотрим вспомогательную функцию.

.

Поскольку функция F (x, y) интегрируемая на области Р и на множестве ПР, то существует двойной интеграл. Аналагично из существования для каждого х интегралов, и следует, что х существует интеграл:. Таким образом функция F (x, y) соответствует всем условиям теоремы 1, а поэтому. Учитывая, что ,=,.

Приходим к формуле (5).

Следствие 2. Если функция f (х, у) непрерывная на области Р, то для яе справедлива формула (2.5).

Следствие 3. Если Р есть область второго типа, т. е., где и — непрерывные на функции, то.

= (6).

Следствие 4. Если Р есть элементарная в отношении двух координатных осей, то её называют элементарной, и при вычислении двойного интеграла по такой области можно пользоваться обеими формулами (5) и (6). Нужно отметить, что в некоторых случаях вычисление двойного интеграла значительно упрощается, если правильно выбрать порядок интегравання.

Замечание 4. Если область интегрирования не является элементарнй в отношении ни одной из координатных осей, то обычно её можно поделить на конечное число областей, элементарных в отношении одной из координатных осей.

Замечание 5. Если при вычилении двойного интеграла удобно перейти от двойного интеграла по области одного типа к двойному интегралу по области второго типа, то такой переход называют заменой порядка интегрирования в повторном интеграле.