Проверка на монотонное изменение значений при обучении геометрии

Основным критерием сознательного усвоения математических знаний является умение оперировать ими при решении задач. Обучение геометрии, направленное на формирование у учащихся практических умений и навыков, требует дальнейшего совершенствования.

Применение и использование наиболее распространенных методов и приемов обучения создает условия для развития познавательных возможностей учеников.

При обучении математике необходимо составить упражнения таким способом, чтобы при их решении школьники не действовали механически, а сознательно вдумывались в каждое новое задание, искали наиболее рациональные способы их решения и умели проверять правильность собственных рассуждений.

Проверка математического знания должна быть всегда доступна пониманию и быть достаточно адекватной ее содержанию. Например, если ответ числовой, то проверка должна проводиться и в соседних значениях. Это дает возможность представить изучаемый материал в сравнении. Проверка в соседних значениях по существу определяет единую физико-математическую природу на предмет изменения в расчетах, т. е. возрастания, убывания или экстремум. В принципе, вариация параметров задачи всегда является полезным и даже универсальным действием. Поэтому мы можем его и назвать универсальным учебным действием (УУД).

Для проверки геометрических теорем или свойств можно использовать фигуру с незначительно измененными параметрами. Например, вместо исходной фигуры взять целочисленную фигуру, приближенно равную заданной. Постановка задачи с целочисленными условиями помогает большинству учащимся лучше понимать содержание данной задачи, а также проанализировать ход ее решения. Значительно легче провести рассуждения при решении задач с целочисленными данными, чем с условиями заданными в общем виде. Проверку теоремы следует проводить непосредственно после логического доказательства. Данный метод создает благоприятные условия для использования фундаментальных закономерностей, оптимизирующих учебный процесс.

Рассмотрим замечательное свойство треугольника с углами 22°30', 67°30', 90°: высота, биссектриса и медиана прямого угла делят его на четыре равные части. Но подлинно, теоретическим фактом это свойство стало после доказательства обратной теоремы: Если в треугольнике высота, биссектриса и медиана, выходящие из одной вершины делят его угол на четыре равные части, то этот треугольник прямоугольный, а значит с углом в 22°30'.

В журнале «Математика в школе» № 2, 1954 года [3] учителем математики Нечунаевской 7-летней школы Алтайского края П. Эрдниевым была предложена задача № 6 с. 94. Треугольник является разносторонним прямоугольным тогда и только тогда, когда биссектриса одного угла является в то же время биссектрисой угла между высотой и медианой того же угла.

И уже в № 4 [4] опубликовано продолжение задачи № 6 из вершины С треугольника ABC проведены высоты CH, биссектриса CL и медиана СH. Определить углы треугольника ABC, если известно, что углы ACH, HCL, LCM и MCB равны между собой (рис.1).

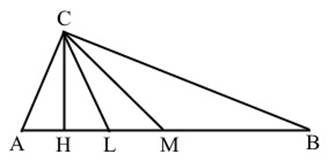
Рис. 1. Чертеж к задаче

Прямоугольный треугольник со сторонами 5,12,13 интересен тем, что тангенс большего острого угла или угловой коэффициент прямой, проходящей через точки A (0;12), B (0;?5) равен k₂=tgB=12/5=2,4. Отсюда? B=67°24'; A=22°4' (рис.2).

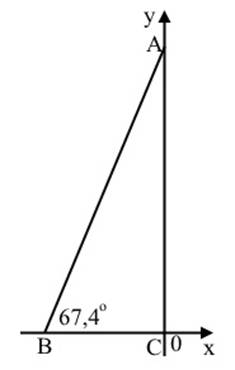
Рис. 2. Треугольник со сторонами 5,12,13

Таким образом, с точностью до 0,1° угол отличается от угла 22°30', а это значит, что треугольник со сторонами 5,12,13 близок к треугольнику 22°30', 67°30', 90° (рис.1). Это невидимое на глаз отличие двух треугольников является важным для понимания сущности математического знания.

Поэтому для проверки на монотонное изменение значений взят прямоугольный треугольник со сторонами 5,12,13 на рис. 2. Углы ACH и ABC равны по 22,4°. Угол ACL равен 45°, тогда? HCL=22,6°. Так как CM=MB, то? LCM=22,4°. Точка М является центром описанной окружности (рис.3).

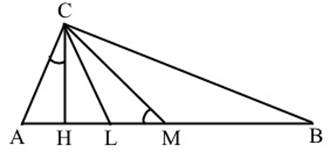
Рис. 3. Проверка свойства на треугольнике со сторонами 5,12,13

Этот способ проверки на практике больше убеждает, чем точное совпадение.

Треугольник со сторонами 5,12,13 и другой с углами 22,5°, 67,5°, 90°заданы в разных единицах измерения: первый в условных метрических единицах, реализуемых на чертеже школьного листа или A4, а второй с заданными транспортиром углами.

Треугольник с углами 30°, 60°, 90° условно можно назвать «полуправильным», как разделенного пополам правильного треугольника с равными соответственно углами по 60° и сторонами, длина которых может быть принята за 2. Если по-другому приложить две половинки по меньшему катету, то получится тупоугольный равнобедренный треугольник с углами 30°, 30°, 120° с соотношением углов 1:1:4. Получили два экономных чертежа (рис.3) с численными характеристиками углов:

tgA=tg60°=v3?1,732, sinA=sin60°=v3:2?0,866.

tgA=tg30°=1:v3=v3:3?0,5773, sinA=sin30°=1:2=0,5.

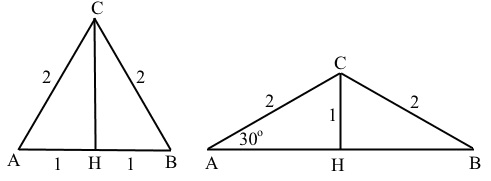
Рис. 4. Полуправильный и тупоугольный треугольники

Значения тангенса и синуса углов представлены как функции с перспективой введения производных (tgx)'=1:cos²x, (sinx)'=cosx, (cosx)'=?sinx.

Поэтому в соответствии с монотонными изменениями значений полезно задавать проверочные на «непрерывность» значения характеристик соседних двух углов 59° и 61°.

Проверка через формулы производных:

• (tg61°?tg59°):2°?(1,804?1,664):0,0349=0,140:0,035=4, cos²60°=(1:2)²=1:4
• (sin61°?sin59°):0,035?(0,8776?0,8572):0,035=0,4986?0,5, cos60°=0,5

В математике важна точность перевода обыкновенных дробей в десятичные. Обыкновенная дробь 8/15=0,5(3) проверяется через прямоугольный треугольник со сторонами 8,15,17 вычислением tgB=15/8=1,875. Первая дробь читается как 0,5 и 3 в периоде, а вторая ей обратная 15/8=1,875 — одна целая, восемьсот семьдесят пять тысячных. По таблице В. М. Брадиса [1] находим, что угол B равен 61°54'. Важно на слух читать не 61 градус и 54 минуты, 61 и 9 десятых градуса. Числа 61 и 54 неравноценны для памяти учащихся. В этом случае десятичная запись значения угла имеет вид: B=61°55'=61,9°. Контрольная сумма 28,1°+61,9°=28°05'+62°55'=90°.

У треугольника со сторонами 8,15,17 синус меньшего угла, А равен 8/17?0,4 705 882 приближенно на 0,03 меньше, чем 0,5.

Цифровые значения двух острых углов важны тем, что в них с точностью до подобия фиксируется форма треугольника со сторонами 8,15,17 близкого до чертежного с углами 30°, 60°, 90°, у которого меньший катет в два раза меньше гипотенузы. Это можно использовать для проверки теоремы, изучаемой в 7 классе.

В книге [5, с.57] для проверки (подтверждения) теоремы после устного доказательства строят фигуру, удовлетворяющую требованию условия теоремы; затем производят измерение соответствующих элементов этой фигуры; наконец, по результатам измерений проверяют, выполняется ли заключение теоремы.

Пусть на уроке была доказана теорема [2, c.76]: Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета равен 30 градусам. Учитель после доказательства проводит беседу.

? Начертите прямоугольный треугольник ABC со сторонами BC=8, AC=15, AB=17, угол C — прямой.

Катет BC приближенно равен половине гипотенузы AB.

? О чем говорится в заключении теоремы?

… угол, лежащий против этого катета равен 30 градусам.

? Измерьте угол A. Градусная мера этого угла приближенно равна 30°.

На основании проведенных измерений возможна ошибка в 1 градус в ту или другую сторону из-за неточности. В этом случае теория подтверждает проведенные измерения и при этом является обобщением опыта.

В заданиях ЕГЭ 2014 была предложена задача С 4. В равностороннем треугольнике проведена высота СН. Через основание высоты проведены перпендикуляры к боковым сторонами НМ и НN. Прямая MN отсекает треугольник СMN.

• 1. Доказать, что треугольник CMN подобен треугольнику ABC.
• 2. Найти отношение площадей треугольника CMN к площади четырехугольника AMNB, если CH=2 и радиус описанной окружности R=4.

Ответ: 1/15.

Условие, что треугольник является разносторонним, с точки зрения логики является избыточным, так как оно не влияет на ход решения задачи. Отношение высоты к радиусу описанной окружности не определяет характеристик произвольного треугольника.

В каждой планиметрической задаче следует проверить наличие пяти видов треугольника: правильного, «полуправильного», равнобедренного, прямоугольного и египетского. В правильном треугольнике высота является медианой. Поэтому R=CO=2CH:3. Отношение СH: CO=3:2. В данной задаче отношению CH: CO=1:2 удовлетворяет равнобедренный тупоугольный треугольник (рис.5).

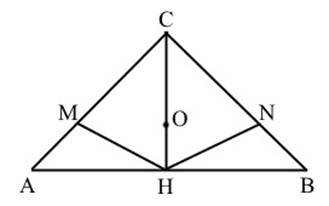
Рис. 5.Равнобедренный тупоугольный треугольник

Рассмотренный метод изменения параметров задачи помогает учащимся лучше усвоить геометрические формы и соотношения, способствует развитию наблюдательности, весьма ценен с точки зрения самой геометрии и методики её преподавания. Известно, что многие учащиеся действуют в любой ситуации по некоторому шаблону. Изменение параметров задачи способствует развитию вариативного мышления.

Библиографический список.

• 1. Брадис В. М. Четырехзначные математические таблицы / В. М. Брадис. — 16-е изд., стереотип. — М.: Дрофа, 2013. — 93, [3] с.: ил.
• 2. Геометрия. 7?9 классы: учеб. для общеобразоват. организаций / [Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. — 2-е изд. — М.: Просвещение, 2014. — 383 с.: ил.
• 3. Математика в школе. — 1954. — № 2.
• 4. Математика в школе. — 1954. — № 4.
• 5. Эрдниев П. М. Развитие навыков самоконтроля при обучении математике. М.: Учпедгиз, 1957, 68 стр.