Исследование функций. 
Исследование функций

Задание 1. Пределы функций

Вычислить пределы:

а) =*=.

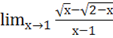
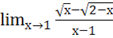
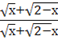
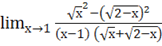
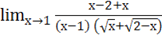
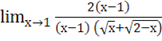
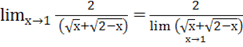
=== = =1.

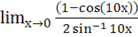
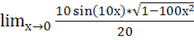
b)= = = 0.

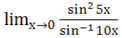
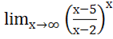
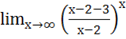
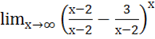
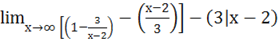
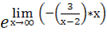
c)= = = ^х ==.

Задание 2. Исследование функций Используя дифференциальное исчисление, провести полное исследование функции и построить ее график: у=.

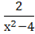
1 Найдем область определения функции.

х²-4=0 х²=4 х=.

2 Исследуем функцию на четность.

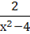
f (-х)== =f (х).

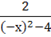
Функция четная значит ее график симметричен относительно оси ординат.

3 Находим вертикальные асимптоты к графику функции.

При х>2 слева =;

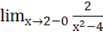
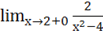
При х>2 справа =+.

х=2 Вертикальная асимптота, т.к. график функции симметричен относительно оси ординат, то прямая х=-2 тоже будет вертикальной асимптотой.

4 Исследуем поведение функции на бесконечность.

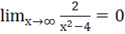
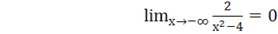
Прямая у=0 является горизонтальной асимптотой.

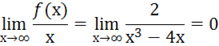
5 Найдем экстремум и интервалы монотонности.

у^'='==.

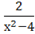
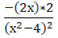
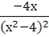
у^'=0 х=0.

Производная не существует в точках х=2 и х=-2, но эти токи не входят в область определения.

На (- у^'>0 следовательно функция на промежутке не возрастает.

На (0;+?) у следовательно функция на промежутке убывает.

у^'

+ - х=0 точка максимума у 0.

6 Находим интервалы выпуклости и точки перегиба функции.

у^''== =-==.

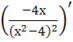
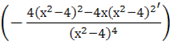
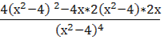
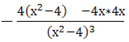
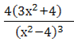
Точек в которых вторая производная обращается в 0, нет, следовательно нет точек перегиба.

3х²+4>0 следовательно знак у^'' зависит от знака (х²-4)³ следовательно на (-2;2).

у^'', на (-?;-2) у^''>0.

у^'' -2 2.

+ - +.

7 Находим точки пересечения графика функции с осями координат.

Пусть х=0 у=.

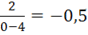
Точка пересечения графика функции с осью ординат (0;-0,5).

Пусть у=0 то таких значений х нет.

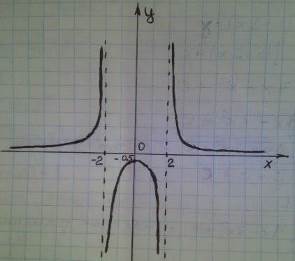
Рисунок 1 График функции у=.

Задание 3 Неопределенный интеграл Вычислить неопределенные интегралы, используя методы интегрирования:

• а) — непосредственное интегрирование;
• б) — замены переменной;
• в) — интегрирования по частям.

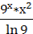
а) = =+2 = + 2* + +C.

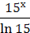
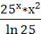
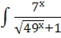
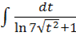
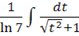
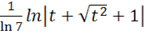
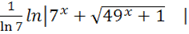
б)dx== = =+C=+С.

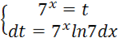
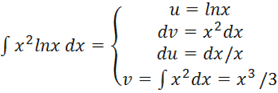
в) = ln x* ;

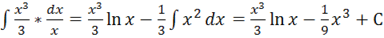
Задание 4 Определенный интеграл.

4.1 Вычислить определенный интеграл:

==.

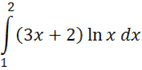
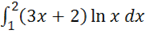
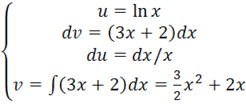
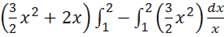
ln x*=ln 2 *(6+4)-ln 1.

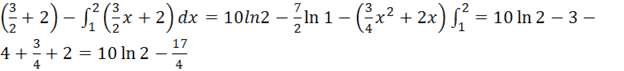
4.2 Вычислить площадь плоской фигуры, ограниченной заданными кривыми. Сделать чертеж.

y=x²+3 x=0 y=x-1 x=2.

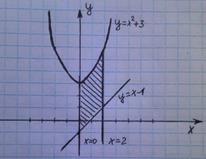
Рисунок 2 чертех фигуры ограниченной кривыми.

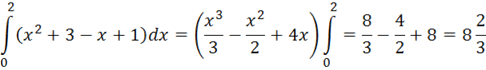
Задание 5 Несобственный интеграл Вычислить интеграл или установить его расходимость:

а).

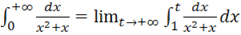
= = ln x.

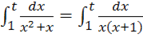
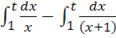
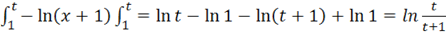
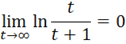
Интеграл сходящийся.

б).

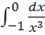
Особая точка х=0.

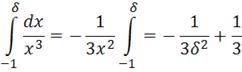
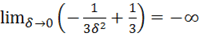
Этот интеграл расходящийся.

Задание 6 Ряды.

6.1 Числовые ряды. Исследовать ряд на сходимость.

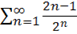
u_n= u_n+1=.

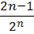
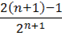
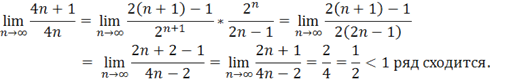
6.2 Степенные ряды. Определить область сходимости степенного ряда.

С_n=3ⁿ(x-2)ⁿ С_n+1=3ⁿ⁺¹(x-2)ⁿ⁺¹

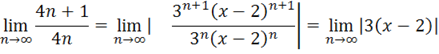
— ¹

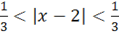
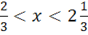
Область сходимости:(.

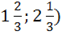
Задание 7 Функции нескольких переменных Исследовать функцию двух переменных на экстремум.

z=.

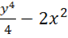
z'_x=-4x z'_y=y³

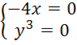
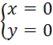
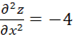
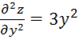
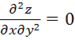
x=0 y=0 A=-4 B=0 C=0.

функция ряд интеграл дифференциальный.

x=0 y=0 не является точкой экстремума.

Задание 8 Решение дифференциальных уравнений.

8.1 Найти общее и частное решения дифференциального уравнения:

y²y'=3−2x y (0)=1.

y²

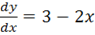
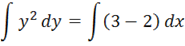
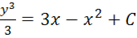
Общее решение.

y (0)=1 1³/3 = 0 — 0 + С С = 1/3.

y³/3 = 3x — x² + 1/3.

y³ = 9x — 3x² + 1 Частное решение.

8.2. Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям:

y''- 6y' + 9y = 0 y (0) = 1 y'(0) = -1.

k² — 6k+9=0 Характеристическое уравнение.

k₁ = k₂ = 3.

y_общ = е ^3x (C₁+C₂ x) Общее решение.

y^/ _общ = 3e ^3x (C₁ + C₂ x) + C₂ e ^3x

y (0) = 1 e ^3*0 (C₁+C₂*0) = 1 C₁ = 1.

y^/ (0) = -1 3*e ^3*0 (C₁+C₂*0) + C₂* e ^3*0 = -1 3*C₁+C₂ = -1 3+C₂ = -1.

C₂ = -4 y_част = е^3x (1−4x).

Список использованных источников

• 1. Аксёнов. Математический анализ.
• 2. Натанзон С. М. Краткий курс математического анализа. 2004 год.
• 3. Письменный Д. Т. Конспект лекций по высшей математике.
• 4. Фомин В. И. Учебное пособие по математике. 2007 год.