Пример экстраполяции в экономическом прогнозировании

В современных условиях развития рыночных отношений, реализации принципов федерализма, становления местного самоуправления возрастает роль региональных демографических прогнозов. Состав демографических факторов, характер их влияния своеобразны для каждого региона. Для одних огромное значение имеет миграционный фактор (Ставропольский край, Ростовская область), для других — природно-климатический (Север России), для третьих — последствия событий прошлых лет (Центральные районы России), для четвертых — национальные особенности (Юг России) и др. Региональные демографические прогнозы разрабатываются на уровне крупных, средних и малых регионов.

В качестве исходных показателей для прогнозирования демографических процессов в Оренбургской области, возьмем показатели:

• -численности постоянного населения на 1 января;
• -число родившихся и умерших человек за год (естественное движение населения);
• -число прибывших и выбывших человек за год (миграционное движение населения), представленные на сайте Федеральной службы государственной статистики РФ.

Рассчитаем прогнозные значения данных показателей, используя методы экстраполяции: скользящих средних. Прогноз должен иметь высокую точность, ошибка прогноза будет тем меньше, чем меньше период (срок) упреждения и чем больше база прогноза.

Период (срок) упреждения — это интервал времени, на который разрабатывается прогноз. База прогноза — это статистическая информация за ряд лет, на которую мы опираемся при построении расчетов. Срок упреждения должен составлять не более 1/3 базы прогноза. В данной работе будем использовать базы прогноза за 19−20 лет и находить прогнозные значения на трехлетний период.

Для оценки точности прогнозов, построенных методом экстраполяции, существуют несколько способов.

Таблица 1. Формулы оценки точности прогнозов методом экстраполяции.

Средняя абсолютная оценка.	Средняя квадратическая оценка.	Средняя относительная ошибка.
Д.	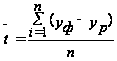е=.
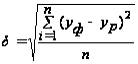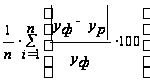Интерпретация значений.
Чем ближе к нулю, тем выше точность прогноза.	е <10 точность высокая. 10<�е <20 хорошая 20<�е <50 удовлетворительная е >50 неудовлетворительная.

Нахождение прогнозных значений методом скользящей средней Одним из наиболее старых и широко известных методов сглаживания временных рядов является метод скользящих средних. Применяя этот метод, можно элиминировать случайные колебания и получить значения, соответствующие влиянию главных факторов. Сглаживание с помощью скользящих средних основано на том, что в средних величинах взаимно погашаются случайные отклонения. Это происходит вследствие замены первоначальных уровней временного ряда средней арифметической величиной внутри выбранного интервала времени. Полученное значение относится к середине выбранного периода. Затем период сдвигается на одно наблюдение, и расчет средней повторяется, причем периоды определения средней берутся все время одинаковыми. Таким образом, в каждом случае средняя центрирована, т. е. отнесена к серединной точке интервала сглаживания и представляет собой уровень для этой точки.

Данный метод используется при краткосрочном прогнозировании. Его рабочая формула:

.

если n = 3 (1).

где t + 1 — прогнозный период; t — период, предшествующий прогнозному периоду (год, месяц и т. д.); yt+1 — прогнозируемый показатель;- скользящая средняя за два периода до прогнозного; n — число уровней, входящих в интервал сглаживания; yt — фактическое значение исследуемого явления за предшествующий период; yt-1 — фактическое значение исследуемого явления за два периода, предшествующих прогнозному.

Для временного ряда показателя «Численность населения на 1 января» определим величину интервала сглаживания: n =3. Рассчитаем скользящую среднюю для первых трех периодов:

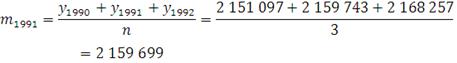
Далее рассчитываем скользящую среднюю для следующих трех периодов:

и т.д.

Составим таблицу расчетов.

Таблица 2 — Расчет прогнозного значения численности населения в Оренбургской области методом скользящей средней.

Годы.	Численность населения Оренбургской областина 1 января, человек.	Скользящая средняя m.	Расчет средней относительной ошибки.
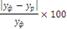	2 151 097.	;	;
	2 159 743.	2 159 699.	0,00.
	2 168 257.	2 170 201.	0,09.
…
	2 137 850.	2 137 920.	0,00.
	2 125 503.	2 127 452.	0,09.
	2 119 003.	2 118 679.	0,02.
	2 111 531.	2 115 267.	;
итого.	43 528 625.	0,85.
прогноз.
	2 116 188.	2 114 949.
	2 117 127.
	2 115 261.
Средняя относительная ошибка ?	0,05.
Средняя абсолютная ошибка Д
Средняя квадратическая ошибка.	1 478.

Рассчитав скользящую среднюю для всех периодов, построим прогноз на 2010 год по формуле (1):

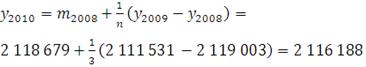
Определяем скользящую среднюю для 2009 года:

.

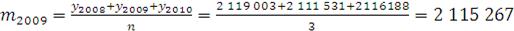
и строим прогноз на 2011 год:

.

чел.

В таблице 2 приведены расчетные данные для определения средней относительной ошибки. Найдем ее значение, разделив на число уровней (n=18):

.

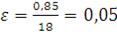
что соответствует высокой точности прогноза.

Полученные результаты представим в таблице.

Таблица 3 — Прогнозные значения абсолютных показателей родившихся, умерших, прибывших и выбывших в Оренбургской области, полученные методом скользящей средней.

Величины средних оценок и средней относительной ошибки позволяют считать точность прогноза достаточно высокой.