Прочность и жесткость вала

Задача № 1.

Расчеты на прочность и жесткость при растяжении-сжатии ступенчатого стержня Требуется:

построить эпюры продольной силы N, нормальных напряжений, перемещений поперечных сечений? l;

определить площадь поперечного сечения стержня из условий прочности и жесткости;

найти перемещение свободного конца стержня;

Исходные данные:

Схема № 9; n=1,5; Р=4кН; а=0,5 м; [] = 140Мпа; [е] = 6· 10−4; Е=1,2· 105Мпа; материал — латунь; г=85 кН/м2.

F=nP.

Решение:

1. Пользуясь методом сечений, определим значения продольных сил N:

сечение 1 — 1.

N1=3 °F =3· 1,5·4=18 кН, сечение 2 — 2.

N2=3 °F — 2 °F — 2 °F = 3· 1,5·4- 4 · 1,5·4= -6 кН.

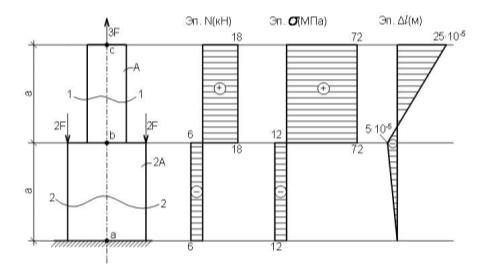
Строим епюру продольных сил.

2. Определяем площадь поперечного сечения из условия прочности на растяжение и сжатие:

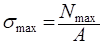
где, А — площадь поперечного сечения бруса.

Опасное сечение — любое сечение участка 1, где = 18кН. Тогда из условия прочности получим:

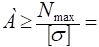
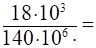
0,129· 10−3м2.

Определяем площадь поперечного сечения из условия жесткости:

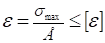
где,.

подставим это значение в условие жесткости:

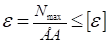
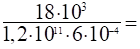
откуда 0,25· 10−3м2.

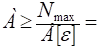
Принимаем наибольшее значение площади из условия жесткости: А=0,25· 10−3м2.

3. Определяем величины нормальных напряжений, пользуясь методом сечений:

сечение 1 — 1.

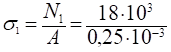
=72 МПа;

сечение 2 — 2.

= -12 МПа;

Строим эпюру нормальных напряжений.

4. Определяем значения перемещений поперечных сечений:

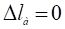
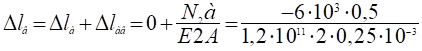
= -510−5 м;

Перемещение свободного конца стержня:

=.

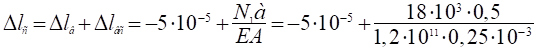
= -510−5 + 3010−5 = 2510−5 м;

5. Определим перемещение свободного конца стержня, с учетом собственного веса стержня:

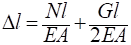
где G=Aгl.

= -510−5 + 0,8 910−5 + 3010−5 + 0,8 910−5=25,17 810−5м.

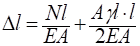
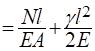
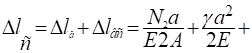
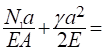
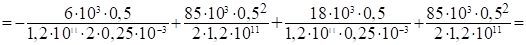
Задача№ 2.

Расчеты на прочность и жесткость при кручении ступенчатого вала Требуется:

• 1) построить эпюры крутящего момента и максимальных касательных напряжений;
• 2) найти размеры поперечных сечений из условий прочности и жесткости;
• 3) определить полный угол закручивания вала;

Исходные данные:

Схема № 9; n1=6; n2=5; n3=2; М=100 Нм; l=0,2 м.

[] = 70Мпа; [и] = 0,5 ?/м; G=8· 104Мпа;

М1=n1M=6· 100=600 Нм;

М2=n2M=5· 100=500 Нм;

М3=n3M=2· 100=200 Нм;

Решение:

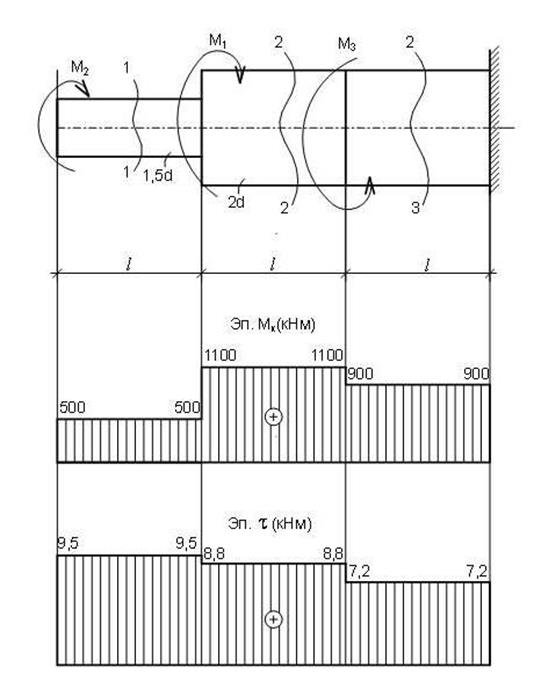
Определяем величину крутящих моментов на участках вала, используя метод сечения. Делаем сечения со стороны свободного конца.

Участок 1 — 1.

Мкр1=M2=500 Нм;

Участок 2 — 2.

Мкр2=M2+ M1=500+600=1100 Нм;

Участок 3 — 3.

Мкр3=M2+ M1- M3=500+600- 200=900 Нм;

Строим эпюру крутящих моментов.

1Из условия прочности при кручении определяем диаметр вала:

Для круга момент сопротивления сечения Wp равен:

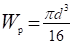
Максимальный крутящий момент равен:

MKP.max = 1100 Нм Подставим эти значения в формулу условия прочности и получим диаметр вала:

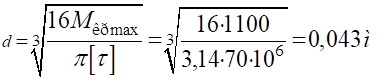
2. Определяем диаметр вала из условия жесткости:

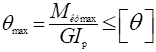
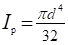
Диаметр вала из условия жесткости:

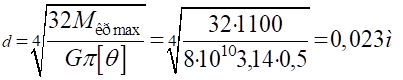
Принимаем диаметр вала из условия прочности d=0,043 м.

3. Определяем касательные напряжения:

Участок 1 — 1.

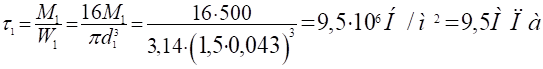
Участок 2 — 2.

Участок 3 — 3.

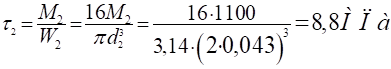
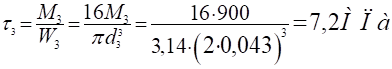
Строим эпюру касательных напряжений.

4. Определяем полный угол закручивания вала по:

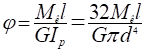
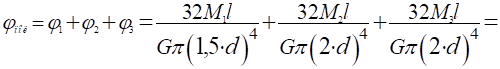
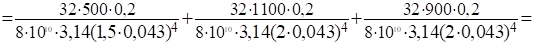
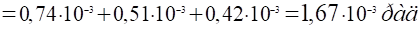
Задача№ 3.

Расчеты на прочность балок при изгибе Требуется:

• 1) построить эпюры поперечной силы и изгибающего момента;
• 2) из условия прочности, определить размеры прямоугольного и стандартного двутаврового сечения балки и сравнить балки с этими сечениями по расходу материала;
• 3) определить наибольшие касательные напряжения в обоих сечениях балки;
• 4) построить эпюры нормальных и касательных напряжений в опасном сечении балки.

Исходные данные:

Схема № 9; h/b=2; n2=-2; k1= -1,5; k2=2; F=2кН; l=0,6 м.

[] = 120Мпа;

F2= n2 F= -2· 2= -4 кН М1= k1 F l = -1,5· 2·0,6= -1,8 к Нм;

М2= k2 F l = 2· 2·0,6= 2,4 к Нм;

Решение:

• 1. Используя уравнение статического равновесия, определяем опорные реакции и:
  • ?МА= М1- F2l — М2+RВ2l=0

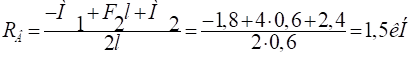
?МВ= - М2+ F2l + М1-RА 2l=0.

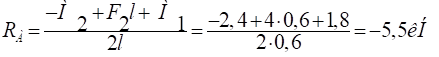
Для проверки, составим уравнение равновесия, относительно оси Y:

?Y=RAF2+ RB= -5,5+4+1,5=0.

Условие выполняется, значит реакции определены верно.

2. Находим значения поперечных сил и изгибающих моментов на каждом участке балки:

Участок 1 — 1.

0? Z1? 0,6.

При Z1=0.

Qу1= RA= -5,5кН;

Мх= RAZ1 — М1= - М1 =1,8 кНм;

При Z1=0,6.

Мх= RAZ1 — М1= -5,5· 0,6 + 1,8 = -1,5 кНм;

Участок 2 — 2.

0? Z2? 0,6.

При Z2=0.

Qу2= -RВ= -1,5кН;

Мх= RВZ2 — М2= - М2 = -2,4 кНм;

При Z1=0,6.

Мх= RВZ2 — М2=1,5· 0,6 -2,4= -1,5кНм;

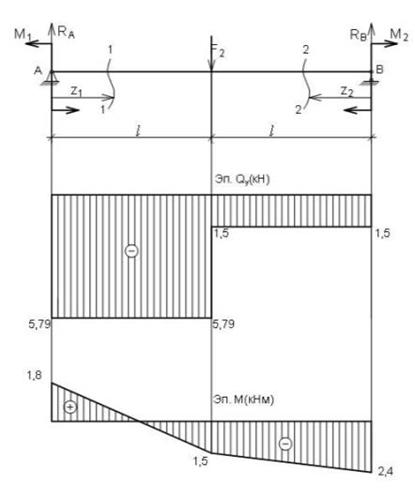
Строим эпюры поперечной силы и изгибающего момента.

3. Определяем размеры прямоугольного и двутаврового сечений балки.

Опасное сечение В, где изгибающий момент — максимален Мх max=2,4 кНм .

Подбираем сечения балки из условия прочности по нормальным напряжениям при изгибе:

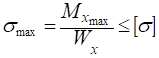
получим формулу проектировочного расчета:

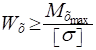
Для прямоугольного сечения.

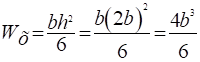
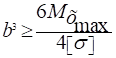
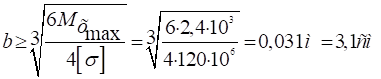
Площадь прямоугольного сечения:

Апр=bh=b2b=2b2=2· 3,12=19,22 cм2.

Для двутаврового сечения:

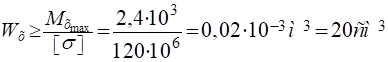
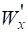
По сортаменту двутавровых балок (ГОСТ 8239−89) подбираем ближайший больший профиль — двутавр № 10 с осевым моментом сопротивления = 39,7 см³ и площадью поперечного сечения Адвут=12 см2, cтатическим моментом отсеченной части сечения = 23 см³.

Сравниваем оба сечения балки по расходу материала:

Адвут: Апр=12:19,22=1:1,6.

Следовательно, двутавровое сечение в 1,6 раза болем экономично, чем прямоугольное сечение.

4. Определяем наибольшие касательные напряжения в обоих сечениях балки, по формуле Журавского. Для этого находим сечение, в котором поперечная сила будет максимальной.

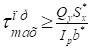
Где, — cтатический момент части сечения, отсекаемой на уровне y от нейтральной линии Максимальные касательные напряжения в обоих сечениях будут находиться на нейтральной линии, где y=0.

Для прямоугольного сечения балки:

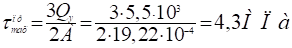
В двутавровом сечении балки:

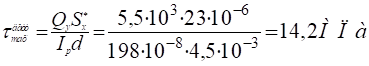
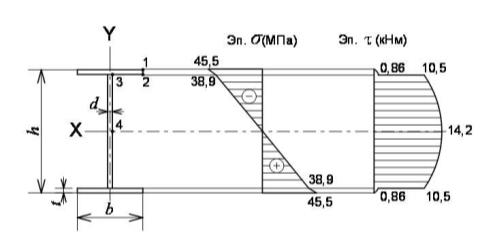
5. Найдем значения касательных и нормальных напряжений в четырех точках опасного сечения балки. При Qоп=5,5кН, Моп=18кНм Из сортамента, для двутавра № 10, находим:

Wx = 39,7 см³; h = 10 см; b = 5,5 см; d = 0,45 см; t = 0,72 см;

1Х = 198 см4; = 23 см³.

Для т.1 у=h/2.

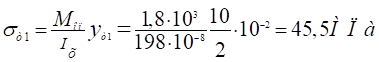
Для т.2.

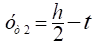
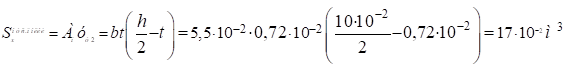
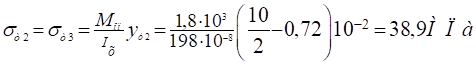
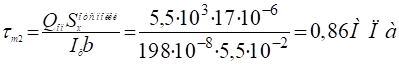
Для т.3.

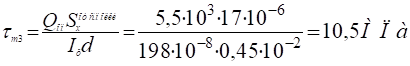
Для т.4.

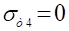
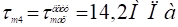
Строим эпюры напряжений.

Задача № 4.

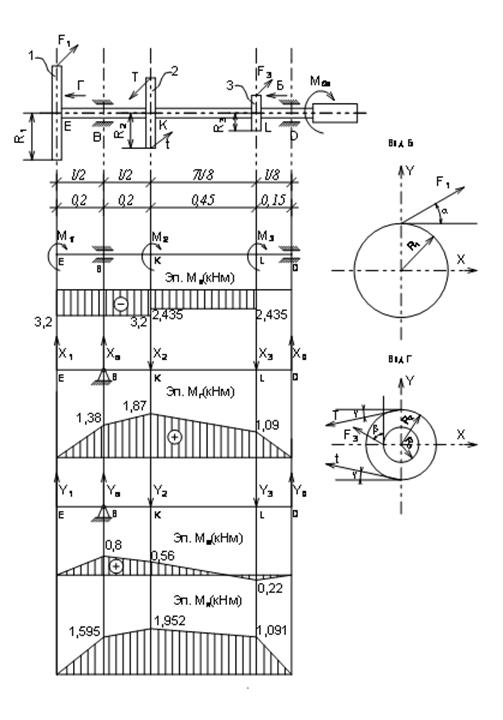
Расчет вала на изгиб с кручением На вал насажены три шкива 1, 2 и 3. На них действуют силы F1, F2, T и t. При равномерном вращении вала, моменты, создаваемые силами, приложенными к шкивам, относительно оси вала, уравновешиваются моментом двигателя Мдв.

Требуется:

найти реакции опор в координатах zAy и zAx;

построить эпюры крутящих моментов и изгибающих моментов в главных областях;

построить эпюры результирующих изгибающих моментов;

найти опасное сечения вала и определить диаметр вала из условия прочности по теории прочности энергии формоизменения.

Исходные данные:

Опоры в сечениях BD; l=1,2 м; R1=0,4 м; R2=0,3 м; R3=0,15 м; б= -30; в=12; г= -60; F1=8кН; F2=6,4кН; Т=3,4кН; n=0,25; [] = 160Мпа Определяем величину крутящих моментов на участках вала и строим эпюру:

М1= F1R1; М2=ТR2 — tR2= ТR2 — nТR2= ТR2(1-n); М3= F2R3.

Величина крутящего момента определяется как при расчете вала на кручение:

• а) Участок ЕК: М1К = -М1 = -F1 R1= -8•0,4= -3,2 кН•м.
• б) Участок КL: М2К = -M1 + M2 =—F1 R1+ ТR2(1-n)= -8•0,4+3,4•0,3(1−0,25) = -2,435 кН•м.
• 2. Строим эпюры изгибающих моментов в горизонтальной и вертикальной плоскостях.

Показываем вал как балку на двух опорах и нагрузим ее силами Х1, Х2 и Х3. |Х1|= F1cosб=8cos30=6,93кН;

|Х2|= Тcosв + nTcosв = 3,4cos12+0,25•3,4cos12= 3,33 + 0,83= 4,16 кН;

|Х3|= F2sinг =6,4sin60= 5,54кН;

Определяем опорные реакции от действия горизонтальных проекций сил, из условия статического равновесия:

МВ: -Х1•0,2 — Х2•0,2 — Х3•0,65 — ХD•0,8 = 0;

XD= (-Х1•0,2 — Х2•0,2 — Х3•0,65) / 0,8=.

=(-6,93•0,2 — 4,16•0,2 — 5,54•0,65)/ 0,8 = -7,27 кН.

МD: X3•0,15 + Х2•0,6 — ХВ•0,8 — Х1•1 = 0;

XВ = (X3•0,15 + Х2•0,6 — Х1•1) /0,8 =.

=(5,54•0,15 + 4,16•0,6 — 6,93) / 0,8 = -4,5 кН.

Знак реакций получили отрицательный — это говорит о том, что предварительное направление опорных реакций выбрано было не верно. Проверка величин полученных реакций:

FX: X1+Хв — Х2 — Х3 — XD = 0;

6,93 — 4,5- 4,16 — 5,54 +7,27= 0;

Условие выполняется, следовательно величины полученных реакций определены верно.

Определяем значение изгибающих моментов во всех точках горизонтальной плоскости:

МD = 0;

МL = - ХD •0,15 = 7,27•0,15 = 1,09 кН•м.

МK = - ХD •0,6 — X3•0,45 = 7,27•0,6 — 5,54•0,45 = 1,87кН•м.

МB = - ХD •0,8 — X3•0,65 — X2•0,2 = 7,27•0,8 — 5,54•0,65 — 4,16•0,2 =.

=1,38 кН•м.

МE = 0.

Аналогично рассмотрим вертикальную плоскость. Показываем вал как балку на двух опорах и нагрузим ее силами У1, У2 и У3.

|Y1|= F1sinб=8sin30=4кН;

|Y2|=| Тsinв — nTsinв| = | 3,4sin12 — 0,25•3,4sin12|= |0,71 — 0,18|= 0,53 кН;

|Y3|= F2cosг =6,4cos60= 3,2кН;

Определяем опорные реакции от действия вертикальных проекций сил, из условия статического равновесия:

МВ: -Y1•0,2 — Y2•0,2 + Y3•0,65 — YD•0,8 = 0;

YD= (-Y1•0,2 — Y2•0,2 + Y3•0,65) / 0,8=.

=(-4•0,2 — 0,53•0,2 + 3,2•0,65)/ 0,8 = 1,47 кН.

МD: -Y3•0,15 + Y2•0,6 — YВ•0,8 — Y1•1 = 0;

YВ = (-Y3•0,15 + Y2•0,6 — Y1•1) /0,8 =.

=(-3,2•0,15 + 0,53•0,6 — 4) / 0,8 = -5,2 кН.

Делаем проверку величин реакций:

FY: Y1 +YB — Y2 + Y3 — YD = 0;

4 — 5,2 — 0,53 +3,2 — 1,47 = 0;

Реакции определены верно.

Вычисляем величины изгибающих моментов в вертикальной плоскости и строим эпюру.

МD = 0;

МL = - YD •0,15 = -1,47•0,15 = -0,22 кН•м.

МK = - YD •0,6 + Y3•0,45 = -1,47•0,6 + 3,2•0,45 = 0,56кН•м.

МB = - YD •0,8 + Y3•0,65 — Y2•0,2 = -1,47•0,8 + 3,2•0,65 — 0,53•0,2=.

=0,8 кН•м.

МE = 0.

3. Определяем величину суммарного изгибающего момента, т.к. изгиб происходит в двух плоскостях — вертикальной и горизонтальной.

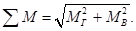
кН•м.

кН•м.

кН•м.

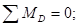
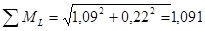
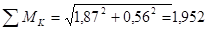
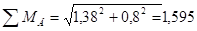
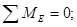
4. Определяем опасное сечение вала.

Таковым, очевидно, будет сечение в точке т.к. здесь мы имеем максимальный суммарный момент = 1,952 кНм и Мк = -3,2 кНм.

Определим максимарный расчетный момент:

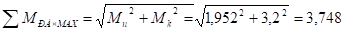
кН•м.

Определяем диаметр вала из условия прочности при совместном действии кручения и изгиба.

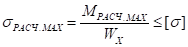
Для круга момент сопротивления площади поперечного сечения вала относительно оси Х:

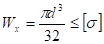
Подставляем значение Wx = 0, ld3 в условие прочности и из него находим диаметр вала.

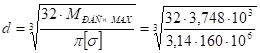
= 0,062 м = 62 мм Принимаем ближайшее большее стандартное значение вала: d = 65 мм.

прочность сжатие ступенчатый вал.