Оператор FOR … NEXT

Слова FOR … NEXT переводятся как «для» … «следующий». Формат оператора таков.

FOR counter = start TO end [STEP increment].

[statementblock].

NEXT [counter [, counter]. .].

Здесь.

counter числовой счетчик, указывающий на количество необходимых операций (повторений),.

start и end начальное и конечное значения счетчика,.

increment шаг, с которым счетчик должен изменяться за один проход цикла,.

[statementblock]блок операторов (в которых переменная счетчика должна использоваться).

Отметим, что начальное и конечное значения, как и собственно шаг, могут быть и (целыми) отрицательными величинами. Для вычисления нашего факториала этот оператор придает программе более простой и прозрачный вид:

' vychislenie faktoriala, n≠1*2*3*…*n.

dim fkt as double.

input «vychilyaem n!; vvedi n (<171)=», n%.

fkt=1.

for i%=1 to n%.

fkt=fkt*i%.

next i%.

print i%;"! = «fkt.

end.

Программа вычисляет факториалы весьма больших чисел (до 170!). Такую организацию циклов можно использовать для очень многих целей. Ниже следуют примеры того, как можно использовать уже известные нам операторы для решения разных задач и нахождения различных величин.

Задача. Найти сумму квадратов первых N членов натурального ряда чисел Решение.

cls.

dim sum as double.

input «vychilyaem summu kvadratov N chisel, N=? «, n%.

for i%=1 to n%.

sum=sum+i%^2.

next i%.

print «summa kvadratov ravna»; sum.

end.

Задача. Распечатать таблицу синусов углов от 0^О до 45^О с шагом 5^О

Решение.

cls.

print «Tablitsa sinusov «.

print «ugol x (grad), sinx «.

for i%=0 to 45 step 5.

print «——————————————————».

print i%, sin (i%*3.141 592 654/180).

next i%.

print «——————————————————».

end.

Давайте попробуем решить одну задачу, настолько же важную, насколько важен для вас ответ на вопрос «Как вычисляют различные функции, например, синусы и косинусы в таблицах Брадиса?». Честно говоря, мне кажется, что понять каким образом вычисляется, например, экспонента (т.е. функция или, как иногда ее записывают) очень важно для понимания всей математики. Если вы вспомните формулу Эйлера.

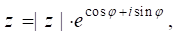
где-то станет ясной та глубокая внутренняя связь, которой связаны второй замечательный предел и вся тригонометрия! Таким образом, ответив на вопрос об экспоненте, мы сможем вычислять и тригонометрические функции.

Формула Тейлора, а вернее ее частный случай — формула Маклорена, дает нам представление экспоненты степенным рядом.

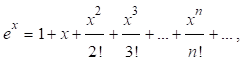
причем ряд этот сходится для всех вещественных. В качестве приближенного значения можно взять некоторую частную сумму этого ряда.

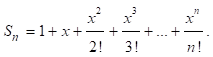
Эта частная сумма приближает истинное значение экспоненты тем лучше, чем большее число мы берем.

Задача. Написать программу, которая бы вычислялаили с желаемой точностью и сверяла результат с тем, который выдает QB.

Решение.

` vechislenie eksponenty.

input «Ishchem znachenie y=exp (x). Vvedi x=»;x.

input «vvedi stepen', do kotoroi schitetsya ryad, n=»;n%.

dim fkt (n%+1) as double, res as double, a as double.

for i%=0 to n%.

gosub fct.

res=res+(x^i%)/fkt (i%).

next i%.

a=exp (x).

print «resul'tat =»;res, «machina daet — «;a.

end.

fct:

fkt (i%)=1.

for j%=1 to i%.

fkt (i%)=fkt (i%)*j%.

next j%.

return.

Десятичная запись чисел, как это нетрудно заметить, является наследием биологического присутствия пяти пальцев на наших конечностях. Поэтому те числа, с которыми мы имеем дело каждый день, абсолютно неестественны с точки зрения математики. С точки зрения информатики именно бинарный способ записи числа есть самый натуральный способ записи. Кроме того, еще более неестественно делить полный круг именно на 360 частей (градусов). Поэтому весь математический анализ функций подразумевает, что их аргументы берутся в радианах. Радианная мера угла столь естественна, что об этом косвенно говорит сам факт отсутствия обозначения этой единицы — с математической точки зрения радианы есть самая натуральная числовая мера угла. Именно поэтому все аргументы всех тригонометрических функций в QB по умолчанию берутся в радианах.

Обратимся к достаточно сложной (но лишь на первый взгляд!) задаче численного интегрирования функций.

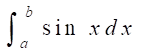
Задача. Вычислить интеграл .

Решение Напомним, что определенным интегралом от функции по промежутку называют предел всевозможных интегральных сумм по всемразбиениям при стремлении длины наибольшего отрезка разбиения к нулю (и, следовательно, при N стремящемся к бесконечности. Частная интегральная сумма для некоторогоразбиения сегмента :

.

.

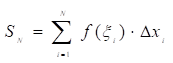
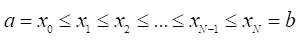
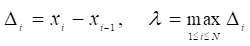
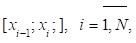
строится так: на каждом элементарном сегментике выбирается точка и вычисляется значение функции в ней. Это значение умножается на ширину сегментика, и затем все такие произведения складываются.

Для целей практического численного интегрирования удобнее разбивать весь сегмент интегрирования не произвольно, а равномерно, т. е. на N равных частей. Все окажутся равными некоторой величине h = (b — a)/N и поэтому это число, уже не зависящее от индекса суммирования, можно вынести за знак суммы как постоянный сомножитель каждого слагаемого.

Далее, в качестве точки также удобно брать, например, самую левую точку или самую правую точку элементарного сегментика. Интегральные суммы, получающиеся при таком выборе значений функции, назовем также левой или правой. Отметим, что при условии возрастания функции на сегменте интегрирования левая сумма становится минимальной для данного разбиения, т. е. нижней суммой Дарбу, в то время как правая сумма есть верхняя сумма Дарбу. При убывании функции все будет с точностью до наоборот. Как известно, критерием существования определенного интеграла является равенство пределов нижних и верхних интегральных сумм Дарбу при неограниченном увеличении числа точек вразбиении и потому стремлении к нулю. Как известно, при увеличении числа точек, участвующих в разбиении, нижняя сумма Дарбу не убывает, а верхняя не возрастает. Более того, для вычисления определенного интеграла можно воспользоваться формулой трапеций, в которой каждое элементарное произведение в интегральной сумме заменяется на площадь трапеции (вертикально поставленной на одну боковую сторону), основаниями которой будут служить значения функции соответственно в левой и правой точках элементарного сегментика. Помня, что ее площадь равна произведению полусуммы оснований на высоту (а высота — это ширина h нашей узкой трапеции), мы замечаем, что в качестве результата формулы трапеций при равномерном разбиении сегмента интегрирования можно взять полусумму левой и правой интегральных сумм. Таким образом, для вычисления определенного интеграла от синуса по произвольному промежутку по формуле трапеций мы можем составить следующую программу:

cls.

print «Vychislenie integrala».

print «b».

print ««;chr$(218) `217? 179.

print ««;chr$(179); «sinxdx».

print ««;chr$(217).

print «a».

Эта часть программы, которую иногда называют «шапкой», создает вводную часть программы. Мы используем функцию chr$(x), которая возвращает на экран символ, отвечающий его десятичному коду x.

Можно было бы написать интеграл и получше, но проблема в том, что при наличии руссификации в системных файлах autoexec. bat и config. sys вторая половина таблицы из 256 выводимых на экран ASCII кодов (Anerican Standard Codes for Information Interchange, произносится как «аски») содержит руссифицированные символы взамен дополнительных символов (которые по старой памяти иногда называют «псевдографикой»), которые бы позволили нам создать более точное изображение знака интеграла.

Далее, введем значения трех параметров, которые и определят результат работы программы:

input «vvedi a»;a.

input «vvedi b»;b.

input «vvedi kolichestvo razbienii, n=»; n%.

Определим с двойной точностью числовые переменные для того, чтобы результат был более надежным:

dim x (n%+1) as double, y (n%+1) as double, h as double.

dim sum as double, lsum as double, rsum as double,.

dim lint as double, rint as double, int as double.

Затем приступим к вычислениям. Помня, что нам нужны и левая, и правая интегральные суммы, мы сначала найдем сумму всех значений функции на всех n + 1 точках разбиения.

for i%=0 to n%.

x (i%)=a+i%*h.

y (i%)=sin (x%) `zdes stoit sama funnktsiya!

sum=sum+y (i%).

next i%.

Теперь можно вычислить левую и правую суммы значений:

lsum=sum-y (n%).

rsum=sum-y (0).

и затем собственно левую и правую интегральные суммы и их среднее.

lint=lsum*h.

rint-rsum*h.

int=(lint+rint)/2.

Теперь можно печатать результат:

print «zpnachenie integrala ravno», int.

end.

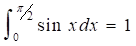
В качестве проверки считается интеграл, в котором величина берется как 3.1 415 926 536 (Можно взять и большее количество знаков в выражении 3.141 592 653 589 793 235 533 824). Нам нужно подставить половину этого числа вместо верхнего предела b. Как это сделать, не выходя из QB для вызова, например, стандартного калькулятора в Windows? Ответ нужно искать на нижней строке интерфейса QB, где имеется подсказка:

Именно клавиша F6, выделенная выше полужирным шрифтом, позволяет перейти из окна редактора в нижнее окошко «Immediate» (сразу, непосредственные вычисления). Однако следует помнить, в этом нижнем окошке можно вводить только одну строку, например:

print 3.1 415 926 536/2 {Enter}.

Появляющийся при этом экран может показать все предыдущие выведенные значения, но самым последним будет именно требуемое число. Запишите его на листочек, перейдите в окно редактора QB, нажав еще раз F6, и затем смело вводите полученный результат.