Задание 3. Биения

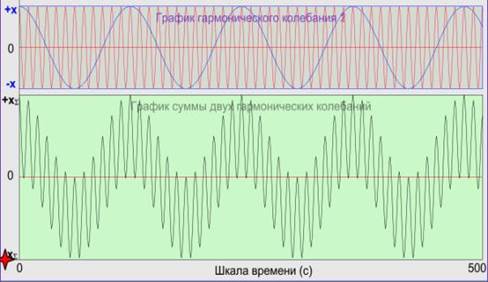
Задайте любое значение периода Т из интервала 9с — 17 с для одного из колебаний, а для другого на 1 с больше или на 1 с меньше. Нажмите кнопку Пуск. Пронаблюдайте за суммарным сигналом. После того как прорисуются графические изображения, совместите векторные диаграммы, слева от графиков, и совместите верхний правый график со средним. Передвигая измеритель вдоль шкалы времени, пронаблюдайте за изменением разности фаз гармонических колебаний от времени. В тех точках временной шкалы, где наблюдаются максимумы и минимумы амплитуды суммарного сигнала, по векторной диаграмме и по совмещенному графику определите, в каких случаях фазы исходных колебаний совпадают, а в каких они находятся в противофазе. На основании наблюдений объясните, за счет чего возникают биения?

Биения возникают при сложении колебаний, отличающихся по частоте на небольшую величину, и проявляются в появлении более низкочастотных изменений амплитуды суммарного сигнала, по сравнению с исходными частотами.

Были ли в исходных гармонических колебаниях медленные изменения амплитуды, как в суммарном колебании, или они возникли в результате сложения?

За счет того, что вращение векторов А1 и А2 происходит с близкими, но отличающимися скоростями, разность фаз этих двух колебаний будет не постоянна, а медленно, то увеличиваться, то уменьшаться. Колебания будут находиться, то в фазе, то в противофазе, в результате амплитуда суммарного сигнала тоже будет меняться.

Зарисуйте график суммарного сигнала и обозначьте на нем период биений Tб.

По нижнему графику модели, используя измеритель, определите период биений Tб, и по нему рассчитайте частоту биений нб = 1/Tб. Рассчитайте по периодам исходных колебаний T1 и T2 частоты н2 и н1. Найдите их разность Дн = н2 — н1 = 1/T2 — 1/T1.Сравните Дн и нб.

Сделайте вывод. На основании вывода заполните таблицу:

Значения н2 или н1 выбираются произвольно, но так, чтобы выполнялось условие для возникновения биений с частотами, указанными в таблице. Будут ли наблюдаться биения, если задать н1 =1Гц и н2 =2Гц?

Если задать н1 =1Гц и н2 =2Гц, то биения не выполняются.

Задание 4. Модуляции

Задайте любое значение периода Т из интервала 120 с — 200 с для одного из колебаний, а другого из интервала 10 с — 20 с. Нажмите кнопку Пуск. Пронаблюдайте за суммарным сигналом. После того как прорисуются графические изображения, поочередно совместите верхние графики с нижним, и оцените, какой вклад вносит каждое из исходных гармонических колебаний. Зарисуйте суммарный график (без исходных сигналов) и отметьте на нем периоды исходных колебаний.

В чем принципиальное отличие модуляций от биений?

При сложении существенно отличающихся по частоте гармонических колебаний говорят о модуляции. В радиосвязи модуляция используется для передачи звукового сигнала. Для этого в передатчике на высокочастотный сигнал накладывается низкочастотный звуковой сигнал. Принимаемая в приемнике высокочастотная составляющая фильтруется, а низкочастотный сигнал подается на динамик для воспроизведения звука.

Контрольные вопросы для проверки усвоения темы лабораторной работы:

1. Что такое колебания? Свободные колебания? Гармонические колебания? Периодические процессы?.

Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебания широко распространены в окружающем мире и могут иметь самую различную природу. Это могут быть механические (маятник), электромагнитные (колебательный контур) и другие виды колебаний.

Свободными, или собственными колебаниями, называются колебания, которые происходят в системе предоставленной самой себе, после того как она была выведена внешним воздействием из состояния равновесия. Примером могут служить колебания шарика, подвешенного на нити. Особую роль в колебательных процессах имеет простейший вид колебаний — гармонические колебания. Гармонические колебания лежат в основе единого подхода при изучении колебаний различной природы, так как колебания, встречающиеся в природе и технике, часто близки к гармоническим, а периодические процессы иной формы можно представить как наложение гармонических колебаний.

Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса.

2. Почему возможен единый подход при изучении колебаний различной физической природы?

Физическая природа колебаний может быть разной поэтому различают колебания механические, электромагнитные и другие. Однако различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Отсюда следует целесообразность единого подхода к изучению колебаний различной физической природы.

3. Дайте определения амплитуды, фазы, начальной фазы, периода, частоты, циклической частоты колебания.

A — амплитуда колебаний (величина наибольшего отклонения системы от положения равновесия); - круговая (циклическая) частота. Периодически изменяющийся аргумент косинуса — называется фазой колебаний. Фаза колебаний определяет смещение колеблющейся величины от положения равновесия в данный момент времени t. Постоянная ц представляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебания. Значение начальной фазы определяется выбором начала отсчета. Величина x может принимать значения, лежащие в пределах отA до +A.

Промежуток времени T, через который повторяются определенные состояния колебательной системы, называется периодом колебаний. Косинус — периодическая функция с периодом 2р, поэтому за промежуток времени T, через который фаза колебаний получит приращение равное 2р, состояние системы, совершающей гармонические колебания, будет повторяться. Этот промежуток времени T называется периодом гармонических колебаний.

Период гармонических колебаний равен: T = 2р/.

Число колебаний в единицу времени называется частотой колебаний н. Частота гармонических колебаний равна: н = 1/T. Единица измерения частоты герц (Гц) — одно колебание в секунду.

Круговая частота = 2р/T = 2рн дает число колебаний за 2р секунд.

4. В чем заключается идея метода вращающейся амплитуды?

Метод вращающейся амплитуды позволяет наглядно представить все параметры, входящие в уравнение гармонических колебаний. Действительно, если вектор амплитуды А расположен под углом ц к оси х (см. Рисунок 1.1. Б), то его проекция на ось х будет равна: x = Acos (ц). Угол ц и есть начальная фаза. Если вектор А привести во вращение с угловой скоростью, равной круговой частоте колебаний, то проекция конца вектора будет перемещаться по оси х и принимать значения, лежащие в пределах отA до +A, причем координата этой проекции будет меняться со временем по закону:.

Таким образом, длина вектора равна амплитуде гармонического колебания, направление вектора в начальный момент образует с осью x угол равный начальной фазе колебаний ц, а изменение угла направления от времени равно фазе гармонических колебаний. Время, за которое вектор амплитуды делает один полный оборот, равно периоду Т гармонических колебаний. Число оборотов вектора в секунду равно частоте колебаний н.

5. Как зависит результат сложения двух колебаний одинакового периода и амплитуды от разности начальных фаз.

Направление (начальная фаза ц) и длина, А вектора амплитуды суммарного гармонического колебания зависит, как от направления (от начальных фаз), так и от длины векторов амплитуд исходных гармонических колебаний.

Если угол (разность фаз: Дц = ц1 — ц2) между векторами А1 и А2 равен 0, то исходные колебания находятся в фазе и суммарная амплитуда (А =А1 +А2) будет максимальна. Если угол (разность фаз: Дц = ц1 — ц2) между векторами А1 и А2 равен — р или р, то исходные колебания находятся в противофазе и суммарная амплитуда (А = А1 -А2) будет минимальна.

6. Поясните биения и модуляцию. В чем их отличие?

Биения возникают при сложении колебаний, отличающихся по частоте на небольшую величину, и проявляются в появлении более низкочастотных изменений амплитуды суммарного сигнала, по сравнению с исходными частотами. Амплитуда колебаний при этом меняется от минимального значения равного разности исходных амплитуд до максимального значения, равного сумме амплитуд исходных колебаний, и вновь до минимального значения. Периодом биений является время повторения этого процесса.

При сложении существенно отличающихся по частоте гармонических колебаний говорят о модуляции. В радиосвязи модуляция используется для передачи звукового сигнала. Для этого в передатчике на высокочастотный сигнал накладывается низкочастотный звуковой сигнал. Принимаемая в приемнике высокочастотная составляющая фильтруется, а низкочастотный сигнал подается на динамик для воспроизведения звука.