Непараметрические критерии. 
Теория вероятностей и математическая статистика. 
Математические модели

Предположим, что для конкретной выборки мы отклоняем гипотезу о нормальном распределении генеральной совокупности. Тогда для получения статистических выводов применяют разные способы. Если объем выборки достаточно велик, то можно использовать параметрические критерии (см. 2.3.2, 2.3.3) как приближенные. Другой способ состоит в подборе замены переменной, приводящей к нормальному распределению. Третий способ — применение непараметрических критериев (часто употребляют термин «критерий, свободный от распределения»), Эти критерии не требуют знания вида исходного распределения F (x), за исключением предположения о том, что это распределение непрерывно. В качестве статистик этих критериев используются такие функции от наблюдений, распределение которых, если верна нулевая гипотеза, не зависит от F (x). Конечно, нельзя ожидать, что непараметрические критерии будут обладать такой же чувствительностью к различению нулевой и альтернативной гипотез, как и критерии, основанные на знании вида F (x). Более подробно с методами непараметрической статистики можно познакомиться в работах [Ю. Н. Благовещенский, В. П. Самсонова, Е. А. Дмитриев, 1989; М.Дж. Кендалл, А. Стьюарт, 1973; Ю. Н. Тюрин, 1978; М. Холлендер, Д. А. Вульф, 1983; J. Н. Zar, 1999].

Наибольшее развитие и применение в задачах непараметрической проверки гипотез получили ранговые методы. Статистики таких критериев основаны не непосредственно на численных значениях наблюдений х, хъ, …,х_п, а на их рангах, т. е. на порядковых номерах наблюдений при их упорядочении по возрастанию (в вариационном ряду), R (xi), R (x2), …, R (x_n). Хотя непараметрические критерии применяются для непрерывных распределений, среди выборочных значений могут быть совпадающие, например из-за неизбежных ошибок округления. В этом случае для определения рангов равных величин используются различные методы. Метод случайного ранга состоит в том, что ранги совпадающих наблюдений можно взять в произвольном порядке. Например, для того чтобы решить, какой из двух равных величин X; или хд, приписать больший ранг, можно бросить монету. Метод среднего ранга каждому из совпадающих наблюдений приписывает ранг, равный среднему арифметическому их порядковых номеров в вариационном ряду. Например, равным величинам х* = хд, которые в случае их неравенства имели бы ранги г и г + 1, приписывается средний ранг г + ½. Третий метод заключается в том, чтобы отбросить равные наблюдения. Ранги наблюдений, будучи функциями выборочных значений, являются случайными величинами с возможными значениями 1,2, …, п. Оказалось, что набор рангов R (xi), R{x₂), …, R{x_n) содержит значительную долю информации о распределении наблюдаемой случайной величины.

Если статистика рангового критерия g{R, R₂, …, R_n) —дискретная случайная величина, то для заданного уровня значимости, а может не существовать значения квантили распределения статистики критерия при справедливости нулевой гипотезы. Поэтому для определения критического множества используются верхнее критическое значение статистики критерия a, равное наименьшему значению квантили распределения статистики критерия д, такому, что Р (д ^ a) ^ а, и нижнее критическое значение д_а, равное наибольшему значению квантили распределения статистики критерия д, такому, что Р (д ^ д_л) ^ а. Значения д_а и <71 __а находят по таблицам. Для всех рассматриваемых далее критериев существуют таблицы критических значений статистики [Л. Н. Большее, Н. В. Смирнов, 1983].

Замечание. Ранговые критерии применяются и в тех случаях, когда наблюдения нс являются количественными, но допускают упорядочение, что часто имеет место в исследованиях по биологии, медицине, психологии и социологии.

Одновыборочные непараметрические критерии

Одновыборочные критерии предназначены для проверки гипотезы о равенстве медианы заданному значению. Пусть имеется выборка xi, X2,. .,?п значений случайной величины? с неизвестной непрерывной функцией распределения F (x, Me), где Me — неизвестная медиана. Требуется проверить гипотезу Щ: Me = Мео, о равенстве медианы заданному числу МеоРассмотрим два наиболее часто используемых критерия для проверки этой гипотезы.

Критерий знаков. В качестве статистики критерия гг⁺ применяют число положительных разностей х* — Мео, t = 1, …, п. Если верна нулевая гипотеза Яо, то Р (х* > Мео) = F{xi < Мео) = = ½ и, следовательно, статистика критерия — дискретная случайная величина, распределенная по биномиальному закону с параметрами п и р = ½.Критическая область уровня значимости, а против двусторонней альтернативы Н: Me Ф Мео будет состоять из двух интервалов [0,п^₂] ^и [^пь-а/2^{, 7г}Ь причем n*f₂ = п — ^{так как} распределение статистики критерия га^-1" симметрично относительно своего среднего п/2, где ⁿa/2^{, n}l-a/2 ^{— нижнее и} верхнее критические значения статистики п⁺ порядка а/2 соответственно. Критическая область против односторонней альтернативы Н Me > Мео имеет вид [nj__a, n] и против односторонней альтернативы Н: Me < Мео ~ [0, raj]. При п —> оо случайная величина га⁺ распределена асимптотически нормально, п⁺ ~ Я (п/2,п/4), и для нахождения критических значений можно воспользоваться нормальным приближением.

Замечание. Критерий знаков обладает недостаточной чувствительностью к различению нулевой и альтернативной гипотез. Но из-за простоты и наглядности он часто используется для предварительного анализа данных. Более мощным является критерий знаковых рангов.

Критерий знаковых рангов. Упорядочим по возрастанию разности Xi — Мео и обозначим через R (xi — Мео) — ранг г-й разности, г = 1, …, п. Статистика критерия знаковых рангов равна сумме рангов положительных разностей ж/ — Мео:

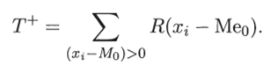
Если нулевая гипотеза Но верна, то вероятность каждого из возможных 2″ исходов для набора рангов положительных разностей равна (½)", что и определяет распределение статистики критерия для заданного п, симметричное относительно среднего п (п + 1)/4, откуда следует, что Т*__а — п (п + 1)/2 — Т+, где Т+, Т+_а — нижнее и верхнее критические значения статистики критерия для заданных, а и п соответственно. Критическая область уровня, а против двусторонней альтернативы будет состоять из двух интервалов [О, г;_/2] и , п (п + 1)/2].

против правосторонней альтернативы — из одного интервала [тГ__в, п (п + 1)/2] и против левосторонней альтернативы — также из одного интервала [0, Т_а⁺ ].

Если верна гипотеза Но, то при п —* ос распределение статистики критерия стремится к нормальному распределению, Т⁺ ~N (п (п + 1)/4, п (п + 1)(2п + 1)/24). При п>25 этим приближением можно пользоваться для определения критических значений статистики.

Проверка гипотезы об отсутствии сдвига

Пусть имеются выборки Ж1, ж₂, …, х_п и у, у2, ?? ?, Ут значений случайных величин I, и т) с неизвестными непрерывными функциями распределения F (x) и G (x) одинаковой формы, которые могут различаться лишь параметром сдвига Д, т. е. G{x) = = F (x — Д). Требуется проверить гипотезу Но '. Д = 0 об отсутствии сдвига между распределениями случайных величин $ и т).

Случай независимых выборок. Пусть Ж1, ж₂, ?? ?, х_п и 1/1,½, ?. •, Ут — независимые выборки.

Критерий Манна — Уитни. Пусть п ^ т, в противном случае выборки поменяем местами. Упорядочим п + т наблюдений по возрастанию и обозначим через R, ранг г-го наблюдения в объединенном ряду наблюдений, i = 1, …, п + т. Если есть совпадающие значения внутри какой-либо из выборок, то их ранги можно взять в произвольном порядке. Если же совпадают значения, принадлежащие разным выборкам, то для определения их рангов применяется метод среднего ранга (см. 2.3.8).

В качестве статистики Манна —Уитни U используется общее число случаев (инверсий) в упорядоченной по возрастанию последовательности из х и у, в которых х появляется позднее некоторого у:

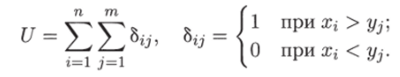
Если Xi = yj, то к значению U прибавляется ½. Статистика U — дискретная случайная величина, принимающая значения от 0 до пт.

Если нулевая гипотеза верна, то С?+_т последовательностей из ж и у являются равновероятными, что и определяет распределение статистики U, симметричное относительно своего среднего пт/2. Критическая область уровня, а против двусторонней альтернативы Н: Д ф 0 будет состоять из двух интервалов [0, ?/_а/2] и [t/i-_a/2, пт], где {/_а/2 и t/i__a/2 — нижнее и верхнее критические значения статистики U порядка а/2 соответственно. Критическая область против односторонней альтернативы Н: А > 0 — из одного интервала [I7i__a, nm] и против односторонней альтернативы Н: Д < 0 — из одного интервала [0, t/_a]. Заметим, что нижнее и верхнее критические значения статистики U связаны соотношением U-_a = тп — U_a.

При малых пит критическое значение U_a определяется непосредственным подсчетом последовательностей с наименьшим количеством инверсий. Если гипотеза Но верна, то при п —> оо, т —> оо статистика U распределена асимптотически нормально: U ~ N (nm/2,пт (п + 1)/12).

Критерий Вилкоксона. Статистику критерия U можно также вычислить по формуле.

где 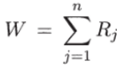, сумма рангов наблюдений Xj, j = 1, —.

статистика критерия Вилкоксона. Следовательно, критерии, основанные на статистиках U и W, эквивалентны.

Пргимер 2.11. Пусть получены выборки значений двух случайных величин $ и Г) объема гг = 4 и то = 5:

Составим из них общий вариационный ряд (т. е. расположим в порядке возрастания), сохранив информацию о принадлежности к выборке:

Сумма рангов выборки значений случайной величины 5 равна И^/ = 1 + 2 + 3 + 6= 12. Это значение не выходит за двусторонние критические пределы № 0,025 = 11 и № 0.975 = 29 уровня значимости 5%. Выборочное значение статистики U = 2 и соответствующее ему р = 0,032 < а = 0,05 и, следовательно, нет оснований отвергнуть нулевую гипотезу о том, что сдвиг между распределениями F (x) и G (x) отсутствует.

Заметим, что приведенные данные были получены с помощью датчика нормально распределенных случайных чисел? ~ N (p = 175, а² = 25) и г) ~ N (i = 180, а² = 25). Приведенные значения могли бы быть, например, значениями роста четырех случайно выбранных французов и пяти случайно выбранных норвежцев (средний рост взрослых мужчин Франции и Норвегии равен 175 и 180 см соответственно), т. е. в действительности сдвиг Д между распределениями отличен от нуля (он равен Д = 175—180 = —5) и гипотеза Но: Д = 0 неверна, но критерии Вилкоксона и Манна—Уитни не обнаружили различия между распределениями F (x) и G (x). Если применить к приведенным данным /-критерий Стьюдента для сравнения математических ожиданий двух нормально распределенных случайных величин с неизвестными дисперсиями, то получим выборочное значение t = —2,72 для статистики критерия. Поскольку это значение выходит за 5%-е критические пределы /7_;о, 025 = —2,36 и <7;0,975 = 2,36 /-распределения с 4 + 5 — 2 = 7 степенями свободы, то гипотеза о равенстве математических ожиданий должна быть отвергнута. Это типичная ситуация — непараметрические критерии обладают меньшей мощностью по сравнению с аналогичными параметрическими критериями, использующими дополнительную информацию о наблюдаемых случайных величинах. Поэтому, если имеется достоверная дополнительная информация, то предпочтительнее использовать критерий, учитывающий эту информацию.

Критерий Ван-дер-Вардена. Обозначим N = п + т. Статистика критерия имеет вид.

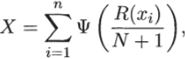
где R (xi) — ранг наблюдения х,; Ф (р) — р-квантиль стандартного нормального распределения.

Критерий Ван-дер-Вардена является наиболее мощным ненараметрическим критерием для проверки гипотезы об отсутствии сдвига. Если обе выборки извлечены из нормальных совокупностей, то при постоянном п и т —? оо критерий Ван-дер-Вардена имеет такую же мощность, как и двухвыборочный ^-критерий.

Случай связанных выборок. Пусть х, Х2,? ??, х_п и у, 2/2i ?? ?, Уп — связанные выборки, например каждая пара наблюдений (xi, yi), i = 1,…,", принадлежит одному объекту, либо (xj, t/i) попарно связаны тем, что условия проведения наблюдений менялись от опыта к опыту, но для каждой пары (Xi, yi) оставались постоянными, что в практике биологического эксперимента встречается очень часто. Обозначим через Zi = — yi,

i — 1, …, п. Тогда проверка гипотезы об отсутствии сдвига между F (x) и С (х) сводится к проверке гипотезы о равенстве нулю медианы для выборки zj, Z2, ?? ?, z_n. Для этого можно применить критерий знаков или критерий знаковых рангов, рассмотренные ранее.

Критерии однородности для независимых выборок. Критерии Манна— Уитни (Вил-коксона) и Ван-дер-Вардена позволяют обнаруживать лишь различия в центральных тенден-i циях непрерывных распределений двух случайных величин. Если важно обнаружить любые расхождения в форме непрерывных распределений, то пользуются критериями однород-¹. пости, например двухвыборочным критерием Смирнова. С помощью этого критерия проверяется гипотеза Н₀: Ft,(x) =? Ец (х) о том, что функции распределения F??x) и Ец (х) случай-! ных величин ?, и ц идентичны против альтернативной гипотезы Н_х: F^(x) *? Fr|(x) о том, что они различны.

Статистика критерия Смирнова D_{m n} определяется как максимум модуля разности между эмпирической функцией F^(.t), построенной по выборке х, хъ, …,х_п, и эмпирической функцией F₄(x), построенной по выборке У, У2, ???, Ут,

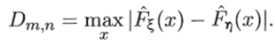
При справедливости гипотезы Но статистика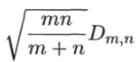

имеет Асимптотическое (при min (ra, п) —> оо так, что отношение т/п остается постоянным) распределение Колмогорова. Критическая область уровня значимости, а против двусторонней альтернативы Н будет состоять из одного полуинтервала [?)_т>пд__а, оо), где Дп, п, i-а ^— квантиль распределения статистики D_mn порядка 1 — а.

Замечание. В англоязычной литературе критерий однородности двух выборок Смирнова называют двухвыборочпым критерием Колмогорова — Смирнова.

Проверка гипотезы о независимости. Пусть имеется двумерная выборка (хь 2/i)> [^Х2, У2), • ••, (^хп, Уп) из неизвестного двумерного распределения. Причем наблюдаемые признаки могут быть как количественными, так и порядковыми. Найдем ранги R (xi) и R (yi) в последовательностях х, хч, …, х_п и УиУ2, • • •, Уп, упорядоченных по отдельности. Мерой зависимости двух случайных величин является коэффициент ранговой корреляции Спирмена, определяемый формулой.

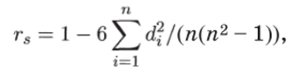
где di = R (xi) — R (yt).

Коэффициент r_s принимает значение от —1 до +1, причем г₃ = 4−1, когда i?(xj) = R (yi), и r₃ = —1, когда последовательности рангов полностью противоположны, т. е. R (xi) = (п 4- 4−1) — R (yi), i = 1, …, п. Для проверки гипотезы независимости признаков, //о, против альтернативы, что признаки зависимы, в качестве статистики критерия используется г₃. Если Щ верна, то распределение статистики г_$ симметрично относительно О с M (r_s) = 0 и D (r_s) = 1/[п — 1). Критическая область уровня значимости, а имеет вид |r₅| ^ ^_s>i-_a/2″ ^гД^{е r}s,i-a/2 ~ верхнее критическое значение статистики критерия r_s порядка а/2.

Если Но верна, то при п —> оо статистика /п — lr_s распределена асимптотически нормально с параметрами (0, 1). При 4 ^ п ^ 10 критические значения статистики критерия находят по таблицам точного распределения г₅, а при п > 10 пользуются нормальной аппроксимацией.