Модель кучи песка

Базовой моделью теории самоорганизованной критичности является куча песка.

Рассмотрим уголок с песком, изображенный на рисунок 1. Будем предполагать сцепление между песчинками достаточно большим. При этом возможно лишь поверхностное перемещение песка, причем инерцией его движения можно пренебречь. Тогда состояние системы вполне определяется наклоном поверхности [ix]. В тех местах, где локальный наклон оказывается больше порога устойчивости, происходит осыпание, приводящее к соскальзыванию песчинок вниз по склону на соседние участки поверхности.

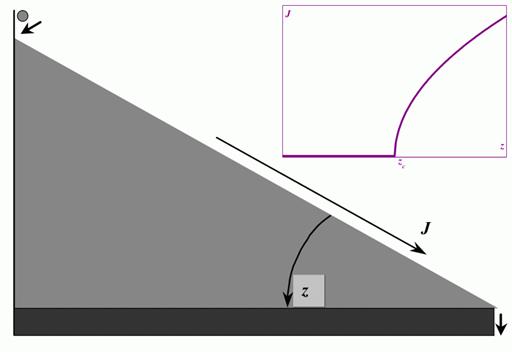
Рисунок 1. Уголок с песком Состояние песка определяется углом наклона поверхности z. При его изменении происходит непрерывный фазовый переход (зависимость параметра порядка от управляющего параметра приведена на врезке) от неподвижного состояния (J = 0) к состоянию непрерывного тока песка (J > 0). При токе J = +0, соответствующем добавлению одной песчинки за один шаг, система самоорганизуется в состояние с критическим наклоном z = zc. Если средний наклон поверхности z невелик, то песок неподвижен. Если же наклон превышает некоторое значение zc, возникает спонтанный ток песка J по поверхности, который непрерывно возрастает при увеличении z (см. врезку на рис. 2). То есть, налицо непрерывный фазовый переход, в котором управляющим параметром является наклон z, а параметром порядка — ток песка J.

Критическое значение наклона zc разделяет хаотическую (z zc) фазы [x]. Обе эти фазы соответствуют некатастрофическому поведению, поскольку в них система устойчива к малым возмущениям. В хаотической фазе они еще быстро затухают во времени и пространстве, а в упорядоченной — уже не могут ощутимо повлиять на величину тока. И лишь в критической точке, где одна добавленная песчинка может вызывать лавину любого размера, возможны катастрофы.

Критическое состояние возникает, когда параметр порядка едва становится ненулевым, т. е. соответствуют моменту его отрыва от нуля. В случае обычных критических явлений такое состояние достигается путем тонкой подстройки. Однако, вместо того чтобы подбирать для управляющего параметра a priori неизвестное критическое значение, можно установить параметр порядка в +0, что заставит управляющий параметр самостоятельно отыскать критическую точку.

Иначе говоря, вместо того, чтобы крутить ручку прибора, можно начать сдвигать с нулевой отметки стрелку на его шкале, вынуждая ручку повернуться до нужного положения [22]. Такое управление параметром порядка обыкновенно достигается при помощи разделения временных масштабов [23], при котором время релаксации системы много меньше времени между последовательными возмущениями, т. е. когда события едва происходят. Самоорганизации кучи песка в критическое состояние происходит при токе J = +0. Чтобы обеспечить такую величину параметра порядка, будем рассматривать динамику по шагам, добавляя песчинки по одной на вершину кучи (см. рис. 2) и дожидаясь завершения процесса релаксации. При этом ток песка через систему, очевидно, имеет минимально возможное значение — в среднем одна песчинка за один шаг рассмотрения.

Если наклон поверхности мал, то лавина, вызванная добавленной песчинкой, скорее всего, не достигнет края кучи и наклон увеличится. При очень большом наклоне состояние кучи является метастабильным, т. е. на любое возмущение она ответит глобальным событием, в результате которого большое количества песка покинет систему и наклон уменьшится. Равновесие между количеством песка, добавляемого в систему, и количеством песка, покидающего ее, достигается при критическом наклоне поверхности, когда возмущение может распространяться по куче сколь угодно далеко, не затухая и не разрастаясь.

Таким образом, имеет место отрицательная обратная связь, вынуждающая наклон принять со временем значениеz = zc вне зависимости от начального профиля поверхности. При этом куча песка, состоящая из локально взаимодействующих песчинок, начинает вести себя как единое целое. То есть, в результате самоорганизации в критическое состояние система приобретает свойства, которых не было у ее элементов, демонстрируя сложное целостное поведение. При этом немаловажно, что самоорганизационная природа целостных свойств обеспечивает их грубость.

Поведение рассмотренной системы может быть пописано на языке клеточных автоматов. Простейшей моделью кучи песка служит автомат, предложенный Д. Дхаром и Р. Рамасвами [24].

Сопоставим куче двумерную гексагональную решетку размером LЧL, горизонтальные слои которой условно соответствуют линиям уровня поверхности. В ячейках решетки расположены целые числа, характеризующие локальный наклон поверхности кучи (см. рис. 3). Если число превышает единицу, ячейка объявляется неустойчивой и осыпается, что выражается в уменьшении на 2 стоящего в ней числа с одновременным увеличением на 1 значений в двух ячейках, примыкающих к данной снизу (рис. 3).

Устойчивыми считаются ячейки с нулевым или единичным наклоном.

Рисунок 2. Простейший клеточный автомат для кучи песка При потере ячейкой устойчивости из нее изымаются две песчинки и передаются в пару нижележащих ячеек. Лавина инициируется добавлением одной песчинки в случайно выбранную ячейку верхнего слоя.

Слева приведено состояние системы до лавины осыпаний, справа — после. Заливкой показаны область лавины и ячейки на ее границе, которые, получив песчинку, сохранили устойчивость.

Шаг моделирования состоит из возмущения и релаксации. Возмущение устойчивого состояния производится путем увеличения на единицу значения в случайно выбранной ячейке верхнего слоя, что соответствует добавлению одной песчинки на вершину кучи. Если в результате возмущения ячейка теряет устойчивость, то она осыпается и начинается процесс релаксации. Осыпание ячейки приводит к увеличению наклона в нижележащих ячейках, что, в свою очередь, способно нарушить их устойчивость и т. д. по принципу цепной реакции. Таким образом, потеря устойчивости одной ячейкой может вызвать лавину осыпаний (рис. 3), продолжающуюся до тех пор, пока все ячейки вновь не обретут устойчивость.

После этого релаксационный процесс считается завершенным и начинается следующий шаг моделирования.

Нижний край решетки является открытым, так что при осыпании ячейки из нижнего слоя две песчинки покидают систему. Это обеспечивает существование стационарного состояния и возможность самоорганизации. Левый и правый края решетки ради простоты отождествлены, т. е. она свернута в вертикальный цилиндр (периодические граничные условия).

Лавины в данной модели распространяются строго сверху вниз, не затрагивая два раза один слой. Поэтому их вполне можно охарактеризовать всего двумя числами: площадью области S, где произошли осыпания, и длительностью T (числом затронутых лавиной слоев). Как показывает компьютерное моделирование, распределение лавин по площади и длительности имеет степенной вид с показателями, соответственно, бS? 0,33 (см. рис. 4) и бT? 0,50 [24].

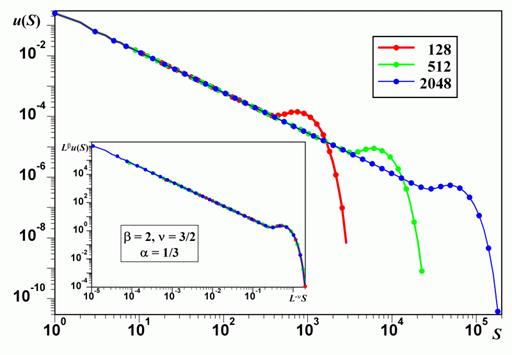
Рисунок 3. Распределение лавин по площади при различных размерах решетки Линейная часть графика, представляющая в двойных логарифмических координатах степенную зависимость, имеет угол наклона приблизительно -1,33. Горб в правой части графиков соответствует тем лавинам, которые оборвались из-за достижения нижнего края решетки.

На врезке приведен конечно размерный скейлинг распределений. Графики, полученные при различных L, совпадают при н? 1,50 и в? 2,00.

Как видно из графиков, приведенных на рис. 4, степенной вид плотности вероятности нарушается при больших значениях аргумента. То есть, вместо формулы (1) следует использовать распределение.

.

где функция h (y) приблизительно постоянна при y << 1 и быстро убывает при больших y. Параметр x1характеризует величину событий, крупных настолько, что они уже не описываются степенной статистикой. Ее нарушение при x ~ x1 обусловлено конечностью размеров системы, из-за чего она и не может порождать сколь угодно крупные события.

Для учета влияния размеров системы на форму распределение обычно применяется метод конечно размерного скейлинга [25]. Он основан на предположении, что плотность вероятности дается формулой.

.

где в и н — скейлинговые показатели, L — размер системы, конечность которого и ограничивает область промежуточной асимптотики, а g (y) — скейлинговая функция, общая для систем различного размера.

Вид формулы (4) обусловлен отсутствием у величины x собственных характерных значений. Поэтому ее характерные значения, определяемые размером системы, зависят от него масштабно инвариантным образом. Например, характерный размер крупного события есть ,.

а среднее событие составляет, как легко видеть,.

.

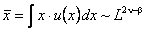
Для эквивалентности формул (3) и (4) необходимо, чтобы в промежуточной асимптотике функция g имела степенной вид.

.

С учетом этого формула (4) сводится к самоорганизованный критичность экономический песочный.

.

А поскольку в промежуточной асимптотике плотность вероятности не зависит от размера системы, показатели оказываются связанными следующим скейлинговым соотношением.

.

Если при построении графиков плотности вероятности, откладывать по оси абсцисс x· L-н, а по оси ординатu (x)· Lв, то графики, соответствующие системам различного размера, совпадут. Таким способом можно с хорошей точностью определить скейлинговые показатели, а через них по формуле выразить и показатель a, для которого в случае распределения лавин по площади получается значение 0,33.

Использование конечноразмерного скейлинга помогает найти значения показателей модели и теоретически [xi].

На каждом шаге в систему добавляется одна песчинка, поэтому в стационарном режиме в среднем одна песчинка будет ее и покидать. Чтобы пройти все L слоев решетки, каждой песчинке необходимо участвовать в L осыпаниях. Поэтому средняя площадь области лавины S, равная среднему количеству осыпаний, будет пропорциональна L .

Откуда, в соответствии с формулами, приходим к следующему соотношению между показателями .

Характерная длительность крупных лавин T1 определяется, очевидно, числом имеющихся в решетке слоев, что дает .

Чтобы объединить соотношения и осталось установить связь между площадью и длительностью лавин. Для этого надо вспомнить, что мы имеем дело с самоорганизованно критической системой.

На каждом слое t, который проходит лавина, она имеет некоторую ширину w (t), определяемую как число осыпавшихся ячеек слоя. Среднее изменение ширины лавины от слоя к слою равно нулю. В самом деле, будь оно отрицательно, вероятность достижения лавиной слоя t экспоненциально бы убывала с его номером, а будь оно положительно, лавина бы с ненулевой вероятностью неограниченно распространялась. Поскольку в первом случае количество песка в системе возрастает, а во втором — убывает, возникает отрицательная обратная связь, подстраивающая систему в критическое состояние. В нем при прохождении лавины по слоям ее ширина изменяется лишь диффузионным образом (как координата частицы, совершающей несмещенные случайные блуждания).

Таким образом, типичная ширина лавины, достигшей слоя t,.

.

Интегрируя эту формулу, находим типичную площадь лавины, достигшей слоя T,.

.

Подстановка в полученную зависимость выражения дает.

.

т.е. нS = 3/2, откуда с учетом соотношения определяется показатель распределения бS = 1/3.

С другой стороны, формула в сочетании с уравнением сохранения вероятности приводит нас к соотношению между показателями распределений и значению бT = ½ в полном согласии с результатами моделирования.

Следствием степенных распределений, описывающих систему, естественно, является ее склонность к катастрофам. В этом смысле очень наглядной является экономическая интерпретация модели [21].

Каждая ячейка рассматривается как экономический агент — производитель определенного вида продукции, для создания двух единиц которой он использует по единице продукции каждого из двух нижележащих агентов. Число в ячейке определяет количество единиц продукции, запрошенной смежниками сверху. Как только накапливается более одного запроса, агент, в свою очередь, посылает по запросу смежникам снизу, чтобы произвести свою продукцию и удовлетворить запросы верхних смежников [xii].

Слои решетки при этом можно трактовать как различные уровни экономики: (внизу — сырьевые и добывающие отрасли, в середине — перерабатывающие, наверху — производители готовой продукции), а добавление единичек в верхний слой — как запрос на единицу товара от конечного потребителя.

Отклик такой модели экономики на элементарное воздействие не имеет собственного характерного размера, и поэтому в ней возможны гигантские события без отчетливых причин, которые можно интерпретировать как кризисы или бумы. И хотя ничто не мешает экономистам a posteriori указать на ту конкретную песчинку, которая сорвала лавину (что обычно и делается при анализе кризисных явлений), причина лавины вовсе не в песчинке, а целостном критическом поведении системы, склонной к катастрофическому поведению.