Теория вероятностей. 
Теория вероятностей

Задание 1.

Из четырех отрезков, длины которых равны 3, 4, 7 и 9 см, наугад выбираются какие-то три. Какова вероятность того, что из выбранных отрезков можно составить треугольник?

Решения: Пусть событие, А — с помощью взятых наудачу трех отрезков можно составить треугольник. По классическому определению вероятности имеем математический дисперсия вероятность.

P (A)=m / n.

Где: m — количество элементарных исходов, благоприятствующих появлению события А;

n — общее число возможных элементарных исходов испытания. равное числу способов, которыми можно отобрать.

Есть всего четыре варианта, из которых два подходят, а два не подходят. Для проверки необходимо использовать неравенство треугольника: a+b>c.

• 1) Если длины отрезков равны 3, 4, 7, то неравенство треугольника не выполняется, т. к. 3+4 =7. Вариант не подходит.
• 2) Если длины отрезков равны 3, 4, 9, то неравенство треугольника не выполняется, т. к. 3+4 < 9. Вариант не подходит.
• 3) Если длины отрезков равны 3, 7, 9 то все неравенствы треугольника выполняются, т. к. 3+7 > 9, 3+9 > 7, 7+9 >3. Вариант подходит, треугольник построить можно.
• 4) Если длины отрезков равны 4, 7, 9 то все неравенствы треугольника выполняются, т. к. 4+7 > 9, 4+9 > 7, 7+9 >4. Вариант подходит, треугольник построить можно.

P (A) = 2 / 4 = 0,5.

Ответ: вероятность того, что из выбранных отрезков можно составить треугольник = 2/4, или 0,5.

Задание 2.

Студент познакомился в троллейбусе с девушкой, и она дала ему свой номер телефона. Однако студент забыл последнюю цифру номера и поэтому набирает ее наугад. Какова вероятность того, что ему придется звонить не более, чем в три места?

Решение:

Первый способ: Вероятность появления события А=1/10 = 0,1. Тогда р = 0,1, q = 0,9.

Студент дозвонился с первого — А 1 раз:

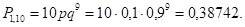
Студент дозвонился со второго — А 2 раза:

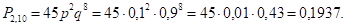
Студент дозвонился с третьего — А 3 раза:

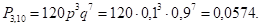
Вероятность того, что студенту пройдется звонить не больше трех раз, равна:

Ответ: вероятность того, что студенту придется звонить не более, чем в три места =0,987.

Второй способ:

Общее число исходов:

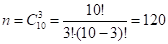
Благоприятное число исходов:

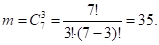
Искомая вероятность: 1-Р=1-m/n=1−35/120?1−0,29?0,71.

Ответ: вероятность того, что студенту придется звонить не более, чем в три места = 0,71.

Задание 3.

На полке стоят 20 учебников, два из них по математике. Наугад выбираются 4 учебника. Найти вероятность того, что хотя бы один их взятых учебников — по математике.

Решение:

По формуле сочетаний.

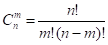
общее число случаев делим на количество благоприятных случаев.

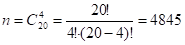
Общее число случаев .

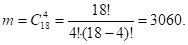
Благоприятное число случаев .

Тогда искомая вероятность того, что хотя бы один из взятых учебников, по математике будет равна:

1-Р=1-m/n=1−3060/4845?0,368.

Ответ: вероятность того, что из 4-х взятых учебников, хотя бы один по математике = 0,368.

Задание 4.

Вероятность того, что спортсмен победит в матче, равна 0,6. Какова вероятность того, что в 10 поединках он одержит больше 8 побед?

Решение:

Пусть событие «А» — спортсмен выиграл матч, = 0,6. Тогда событие «В» — спортсмен проиграл поединок, его вероятность 1−0,6 = 0,4. Тогда, решение будет иметь вид:

Вероятность победы в матче, А р = 0,6, следовательно вероятность проигрыша q = 0,4.

Ответ: вероятность того, что спортсмен из 10-и поединков одержит победу в более 8-и ровна 0,037.

Задание 5.

В первой урне 7 белых шаров и 3 черных, во второй — 4 белых и 5 черных. Из первой урны наугад вынули 2 шара и положили во вторую. Какого цвета шар теперь более вероятно вынуть из второй урны?

Решение:

Введем следующие обозначения для событий:

• 1) из первой урны вынули два белых шара, тогда во второй урне: Р_бел. = 6/11? 0,54; Р_чёр.= =5/11? 0,45
• 2) из первой урны вынули белый и черный шары, тогда во второй урне: Р_бел.= 5/11? 0,45; Р_чёр. = 6/11? 0,54
• 3) из первой урны вынули два чёрных шара, тогда во второй урне: Р_бел. = 4/11? 0,36; Р_чёр.= =7/11? 0,63

Средняя вероятность белых шаров во второй урне:

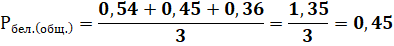
Средняя вероятность чёрных шаров во второй урне:

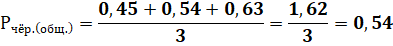
Ответ: более вероятно вынуть из второй урны шар чёрного цвета Р_чёр. = 0,54.

Задание 6.

Нужные сборщику детали находятся в трех из пяти ящиков. Сборщик вскрывает ящики до тех пор пока не найдет нужные детали. Составить закон распределения случайной величины Х — числа вскрытых ящиков. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.

Решение:

Составим следующую вероятность событий: Р₃ — сборщик вскрыл три ящика; Р₂ — сборщик вскрыл два ящика; Р₁ — сборщик нашел деталь в первом ящике.

Р₃=0.4*0.4*0.6*0.6*0.6=0,3 456*5=0,1728.

Р₂=0.4*0.6*0.6*0.6*0,6=0,5 184*5=0,2592.

Р₁=0.6 Закон распределения:

Проверка: 0,6+0,2592+0,1728=1.

Математическое ожидание вычисляется как сумма произведений всех значений x на соответствующие вероятности.

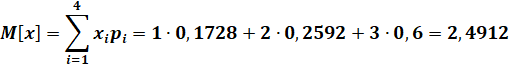
Дисперсия находится по формуле:

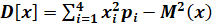
. Дисперсия D[X]:

D[X] = 1²*0,1728 + 2²*0,2592 + 3²*0,6 — 2,4912² = 0,1728+1,0368+5,4- -6,2=0,41.

Среднее квадратическое отклонение у (x).

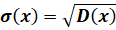
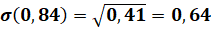
Задание 7.

Случайная величина Х задана функцией распределения F (X). Найти плотность распределения, математическое ожидание, дисперсию, а также вероятность попадания случайной величины в интервал (б, в). Построить графики функций F (X) и f (X).

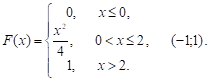
Случайная величина Х задана функцией распределения F (x):

0, x? 0.

x²/4, 0 < x < 2.

1, x > 2.

Найдем плотность распределения f (x), как производную от функции распределения F (x):

f (x) = dF (x)/dx = ½*x.

Плотность распределения f (x):

• 0, x? 0
• ½*x, 0 < x < 2
• 0, x? 2

Математическое ожидание:

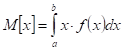
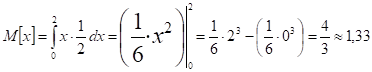
Дисперсия:

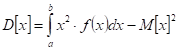
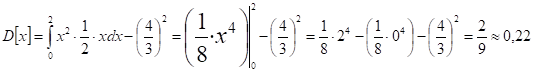
Среднеквадратическое отклонение:

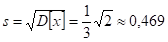
Вероятность попадания случайной величины Х в интервал (б, в).

P (a? X < b) = F (b) — F (a).

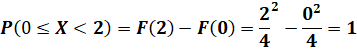
• 1. Вентцель, Е. С. Теория вероятностей / Е. С. Вентцель М.: Наука, 2009 г.
• 2. Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике / В. Е. Гмурман. М.: Высшая школа, 2012 г.
• 3. Коржавина Н. В., Петрова С. А. Теория вероятностей: учеб.-метод. комплекс для студентов всех специальностей / М-во образования и науки РФ, УрГЭУ, Центр дистанционного образования. — Екатеринбург: УрГЭУ 2011 г. — 52 с.