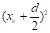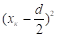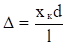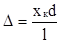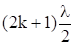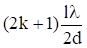Расчет интерференционной картины от двух когерентных источников

Для рассмотренных случаев расчет интерференционной картины можно провести, используя две узкие параллельные щели, расположенные достаточно близко друг к другу (рис. 10).

Щели s₁ и s₂ находятся на малом расстоянии d друг от друга и являются когерентными источниками света.

Луч от источника s'₂ до произвольной точка, А на экране, в которой наблюдается явление интерференции, проходит путь s₂, а от источника s'₁ — путь s₁. Проведем перпендикуляр s'₁С к прямой s'₂А.

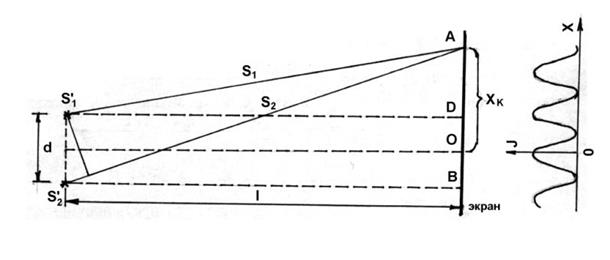
Рис. 10.

Длина прямой s'₁А равна длине прямой СА, т.к. d «l. Тогда отрезок Д = s'₂C будет разностью хода двух лучей до точки, А и будет определять интенсивность света в ней.

д? s₂ — s₁.

Из треугольника s'₂АВ:

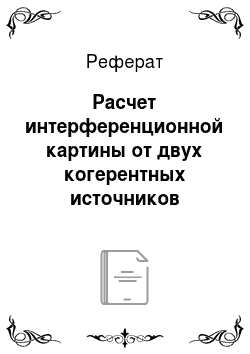
s²₂ = l² +.

Из треугольника:

s'₁АD: s²₁=l²+.

s²₂ — s²₁ = 2х_кd;

(s₂ — s₁)(s₂ + s₁) = 2х_кd; s₂ — s₁ = .

Из условия, что d «l можно считать, что s₂ + s₁? 2l, поэтому разность хода равна:

.

Используя условия максимума и минимума, можно записать:

Для максимума:

=к л, откуда расстояние от центра картины х_кmax до максимума к-го порядка:

х_кmax =, (к = 0, 1, 2, …);

Для минимума:

= ,.

х_кmin =, (к = 0, 1, 2, …).

Этими формулами определяют расстояние х_к светлых (max) и темных (min) полос от центра на экране в случае интерференции от двух источников.

На рис. 10 справа показано распределение интенсивности света в интерференционной картине на экране. Если требуется определить расстояние на экране между к-ой и m-ой полосами на экране, то:

— в случае светлых полос:

Дx_m-k = x_m — x_k = (m — k) ,.

— в случае темных полос:

Дx_m-k = x_m — x_k = (m — k) .

Расстояние между двумя соседними максимумами и двумя соседними минимумами называется шириной интерференционной полосы и определяется по формуле:

Дx = .

При d? л интерференционные полосы становятся неразличимы.

По измеренным значениям l, d и Дx можно определить длину световой волны. Интерференционная картина от двух монохроматических источников представляет собой чередование светлых и темных полос, от источников белого света будут наблюдаться радужные полосы.