Задачи по основным разделам теории вероятностей

Задание № 6

Из трех орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле только из первого орудия равна 0,7; из второго — 0,6; из третьего — 0,8. Найти вероятность того, что: 1) хотя бы один снаряд попадет в цель; 2) только два снаряда попадут в цель; 3) все три снаряда попадут в цель.

Решение:

дано 3 вероятности попадания: p1=0,7 p2=0,6 p3=0,8.

Соответственно, противоположно им 3 вероятности промаха вычисляются по формуле.

q=p=1-p.

q1=1−0,7=0,3; q2=1−0,6=0,4; q3=1−0,8=0,2.

Составим производящую функцию:

(z)=(p1z+q1)*(p2z+q2)*(p3z+q3).

подставим значения.

• (z)=(0,7z+0,3)*(0,6z+0,4)*(0,8z+0,2)
• (z)=0,336z3+0,452z2+0,188z+0,024

По коэффициентам получаем:

Р (3)=0,336 вероятность что все три снаряда попадут в цель;

Р (2)=0,452 вероятность что только два снаряда попадут в цель;

Р (1)=0,188 вероятность что только один снаряд попадет в цель;

P (0)=0,024 вероятность что ни один снаряд не попадет в цель.

Контроль по формуле:

Р (3)+Р (2)+Р (1)+Р (0)=1.

0,336+0,452+0,188+0,024=1.

Вероятность, что хотя бы один снаряд попадет в цель есть противоположное вероятности что ни один снаряд не попадет в цель, то есть Р=1-Р (0)=1−0,024=0,976.

Задание № 16

Задана непрерывная случайная величина Х функцией распределения F (x). Требуется: 1) найти плотность распределения вероятностей f (x); 2) схематично построить график функций f (x) и F (x); 3) найти математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х; 4) найти вероятность того, что Х примет значение из интервала (б;в).

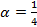
Дано: F (x)= ,.

Решение:

а) Плотность распределения равна первой производной от функции распределения:

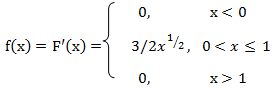
Заметим, что при производная F'(x) не существует.

б) График функции F (x)

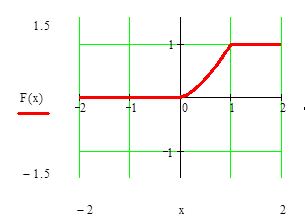
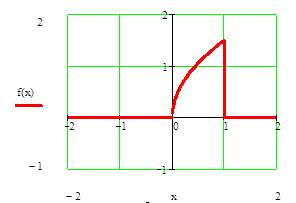
График функции f (x).

в) Математическое ожидание непрерывной случайной величины X, когда все возможные значения принадлежат интервалу, а вне этого интервала, равняется:

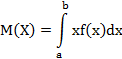
В данном случае:

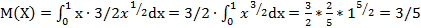
=0.6.

Дисперсия непрерывной случайной величины X, возможные значения которой принадлежат интервалу, равняется:

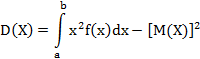
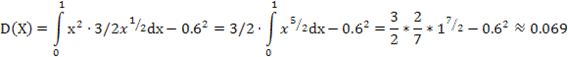
Среднеквадратическое отклонение непрерывной случайной величины X определяется так же, как и для дискретной величины:

В данном случае:

г) Вероятность того, что X примет значение, заключенное в интервале, равна приращению функции распределения на этом интервале:

В данном случае:

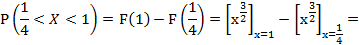
Ответ:

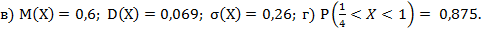
Задание № 26.

Заданы математическое ожидание, а и среднее квадратическое отклонение у нормально распределенной случайной величины Х. Написать плотность распределения вероятностей и схематично построить график. Найти вероятность того, что Х примет значение из интервала (б;в). Определить приближенно максимальное и минимальное значение случайной величины Х, следуя правилу «трех сигм». Найти вероятность того, что Х примет значение, превышающее в; найти интервал, симметричный относительно математического ожидания а, в котором с вероятностью г будут заключены значения случайной величины Х.

Дано: а=10, у=4, б=6, в=18, г=0,90.

Решение:

а) Так как случайная величина X имеет нормальный закон распределения, то плотность распределения имеет вид:

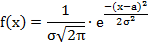
По условию и, тогда:

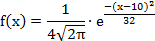
График плотности распределения вероятностей.

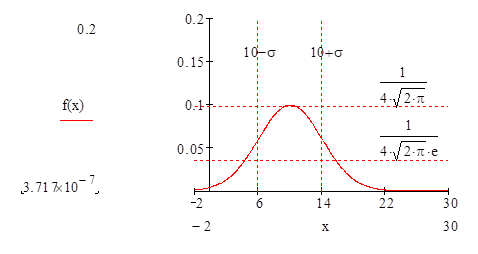
б) Воспользуемся формулой:

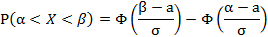
По условию, тогда:

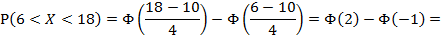
в) По правилу «трёх сигм» событие является практически достоверным событием.

По условию, тогда:

Таким образом, по правилу «трёх сигм» :

г) Оценим :

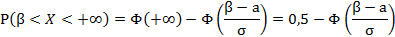
Таким образом, в данном случае:

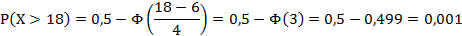
д) Оценим.

Найдём из последнего условия .

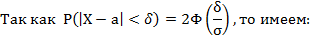
По условию, тогда:

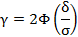
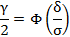
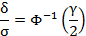
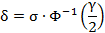
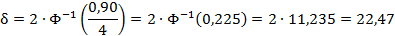
Тогда искомый интервал имеет вид:

или или.

Ответ:

• б) ;
• в) ;
• г)
• д)

Задание № 36

Заданы среднее квадратическое отклонение у нормально распределенной случайной величины Х, выборочная средняя и объем выборки n. Найти доверительный интервал для оценки неизвестного математического ожидания a с доверительной вероятностью г=0,95.

Дано: хВ=25,62; n=64; у=10.

Решение:

Требуется найти доверительный интервал:

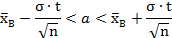
Все величины, кроме t, известны. Найдём t из соотношения:

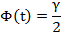
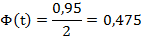
Подставив, получаем:

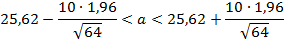
Ответ:

Задание № 46

В результате проверки n контейнеров установлено, что число изделий Х, поврежденных при транспортировке и разгрузке, имеет эмпирическое распределение, сведенное в таблицу, где xi — количество поврежденных изделий в одном контейнере, n — частота этого события, то есть число контейнеров, содержащих Xi поврежденных изделий. При уровне значимости, а требуется проверить гипотезу о том, что случайная величина Х распределена по закону Пуассона. Использовать критерий согласия Пирсона (Х 2).

Дано: n=100; а=0,05.

.

Решение:

Найдём выборочную среднюю:

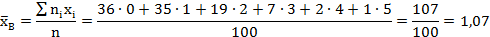
Используем закон Пуассона:

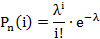
Примем в качестве оценки параметра распределения Пуассона выборочную среднюю: .

Следовательно, закон Пуассона имеет вид:

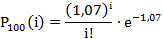
Положив, найдём вероятности появления повреждённых изделий в 100 контейнерах:

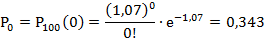
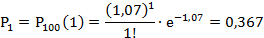
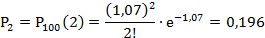
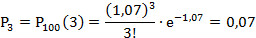
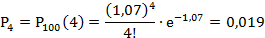
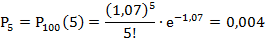
Найдём теоретические частоты по формуле:

Подставив в эту формулу найденные значения вероятностей, получим:

Сравним эмпирические и теоретические частоты с помощью критерия Пирсона. вероятность математический статистический закономерность Для начала объединим малочисленные частоты и соответствующие им теоретические частоты:

и.

Далее составим расчётную таблицу:

Из расчетной таблицы находим наблюдаемое значение критерия Пирсона:

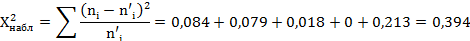
Определяем число степеней свободы, где s число различных групп выборки:

Далее по таблице критических точек распределения находим критическую точку правосторонней критической области, при и :

Ответ: так как, то нет оснований отвергнуть гипотезу о распределении случайной величины X по закону Пуассона.

Задание № 56

Данные наблюдений над двумерной случайной величиной представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X.

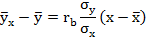X. Y.

Решение:

Составим корреляционную таблицу в условных вариантах, выбрав в качестве ложных нулей и (каждая из этих вариант расположена примерно в середине соответствующего вариационного ряда).

Найдём :

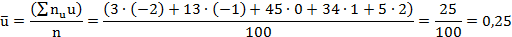
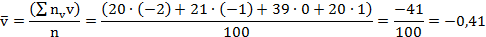
Найдём вспомогательные величины :

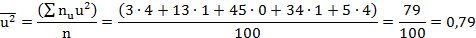
Найдём :

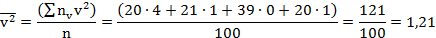
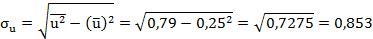
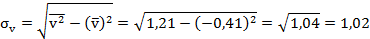
Найдём, для чего составим расчётную таблицу.

u. v.	— 2.	— 1.
— 2.	-6 3 -6	-8 8 -16	9 -18	— 14.
— 1.	-5 5 -5	0 16 -16	— 5.
	0 20 0	17 17 0	4 2 0
17 17 17	6 3 3
— 6.	— 21.	— 34.
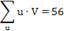					Контроль.

Суммируя числа последнего столбца, находим:

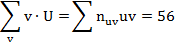
Для контроля вычислений находим сумму чисел последней строки:

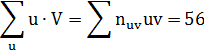
Совпадения сумм свидетельствует о правильности вычислений.

Найдём искомый выборочный коэффициент корреляции:

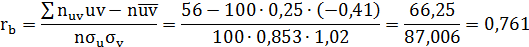
Найдем шаги (разности между любыми двумя соседними вариантами):

;

Найдём, учитывая, что и :

Найдём :

Подставив найденные величины в заданное по условию соотношение, получим искомое уравнение прямой линии регрессии Y на X:

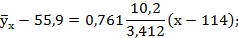
Или окончательно:

Ответ:

Задание № 66

Найти спектральную плотность стационарной случайной функции X (t), если ее корреляционная функция имеет вид:

Решение:

Используем формулу Винера — Хинчина:

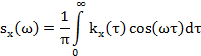
Учитывая, что в интервале, имеем:

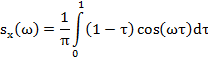
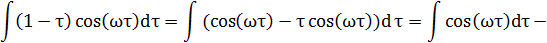
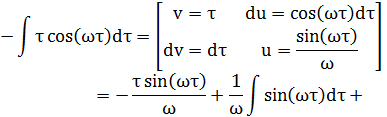
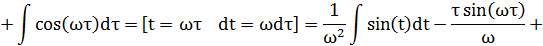
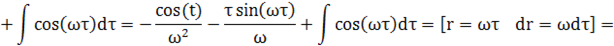
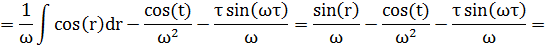
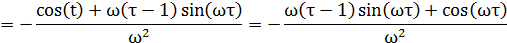
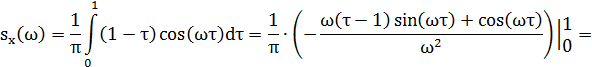
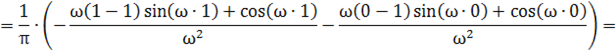
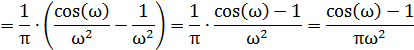
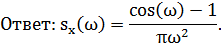
Задание № 76.

На вход линейной стационарной динамической системы, описываемой данным дифференциальным уравнением, подаётся стационарная случайная функция X (t) с математическим ожиданием и корреляционной функцией. Найти: а) математическое ожидание; б) дисперсию случайной функции Y (t) на выходе системы в установившемся режиме.

Решение:

а) Приравняем математические ожидания левой и правой частей заданного дифференциального уравнения:

По условию, X (t) и Y (t) — стационарные функции, а математическое ожидание производной стационарной функции равно нулю, поэтому:

Значит искомое математическое ожидание равно:

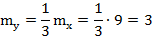
б) Найдём спектральную плотность, при :

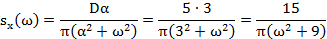
Найдем передаточную функцию системы. Для этого запишем заданное дифференциальное уравнение в операторной форме:

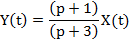
Следовательно, передаточная функция равна:

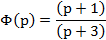
Найдём частотную характеристику системы, для чего положим :

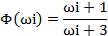
Найдём спектральную плотность на выходе системы, для чего умножим спектральную плотность на квадрат модуля частотной характеристики:

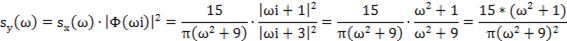
Найдём искомую дисперсию:

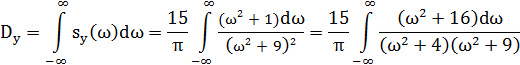
Представим подынтегральную функцию в виде суммы:

Ответ: а); б) .