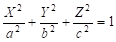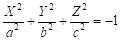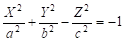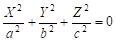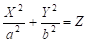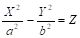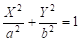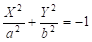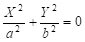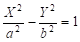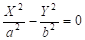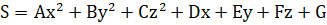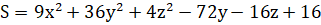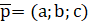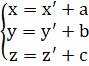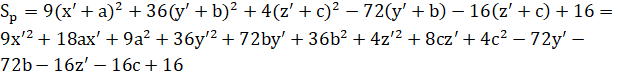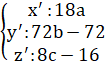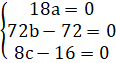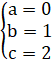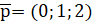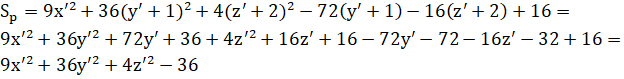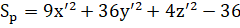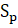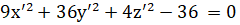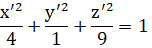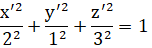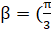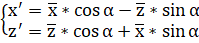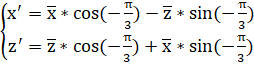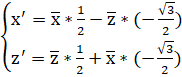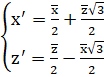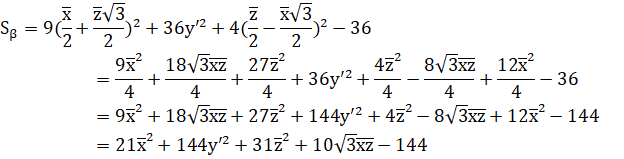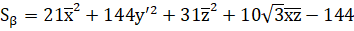Исследование формы поверхности второго порядка

Поверхностью второго порядка S называется геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида:

(2*),.

где по крайней мере один из коэффициентов отличен от нуля.

Уравнение (2*) называют общим уравнением поверхности второго порядка S, а систему координат Oxyz называют общей системой координат.

Теорема 2. Для произвольной поверхности S, заданной общим уравнением существует такая декартова прямоугольная система координат что в этой системе поверхность S имеет уравнение одного из следующих семнадцати канонических видов.

1) — эллипсоид,.

• 2) — мнимый эллипсоид,
• 3) — однополостный гиперболоид,
• 4) — двуполостный гиперболоид,
• 5) — конус,
• 6) — мнимый конус (точка),
• 7) — эллиптический параболоид,
• 8) — гиперболический параболоид,

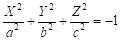
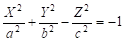
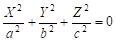
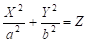
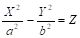
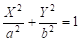
9) — эллиптический цилиндр,.

10) — мнимый эллиптический цилиндр,.

11) — две мнимые пересекающиеся плоскости (ось.

O’Z),.

12) — гиперболический цилиндр,.

• 13) — две пересекающиеся плоскости,
• 14) — параболический цилиндр,
• 15) — две параллельные плоскости,
• 16) — две мнимые параллельные плоскости,
• 17) — две совпадающие плоскости (плоскость XOZ).

В выше перечисленных уравнениях a, b, c, p — положительные параметры. Систему координат называют канонической.

Исследование формы поверхности второго порядка методом сечения плоскостями Если дано каноническое уравнение поверхности S, то представление о поверхности можно получить по форме линий пересечения ее плоскостями:

Z = c — параллельными координатной плоскости XO’Y,.

X = c — параллельными координатной плоскости YO’Z,.

Y = c — параллельными координатной плоскости XO’Z.

Задание 4. Исследование поверхности 2-го порядка методом сечений.

а).

Путём преобразования параллельного переноса получаем:

Решаем полученную систему уравнений:

Чтобы перенести кривую на какой-либо вектор, нужно начало координат перенести на этот вектор, либо вычесть его. Путём преобразования параллельного переноса получаем:

Преобразуем уравнение к каноническому виду:

/36.

в итоге получим каноническое уравнение эллипсоида (см. рис. 7.1−7.4).

Вывод: метод сечения позволяет определить вид поверхности 2-го порядка.

Задание 5. Преобразование координат в пространстве.

Найдём кривую, полученную из кривой поворотом вокруг начала координат (против часовой стрелки) на угол) и на ось y (ось вокруг которой совершается поворот).

При повороте эллипсоида вокруг начала координат против часовой стрелки на угол) и на ось y (ось вокруг которой совершается поворот), уравнение эллипсоида приобрело следующий вид: