Решение задач линейного программирования

1. Решение задач линейного программирования в OpenOffice.org Calc

В данном пункте мы изучим возможности пакета OpenOffice.org Calc при решении задач линейного программирования.

ПРИМЕР. Решить задачу линейного программирования:

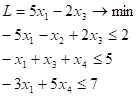
Для решения подобных задач в OpenOffice.org Calc предназначена команда Поиск решения из меню Сервис.

В случае если этот пункт подменю отсутствует, необходимо просто установить расширение scsolver.uno.oxt (http://kohei.us/ooo/solver). Последняя версия Solver (от 28 ноября 2007 года) позволяет решать задачи как линейного, так и нелинейного программирования. Эта версия стала более стабильной, кроме того появилась поддержка русского языка. Для этого выполните команду в окне OpenOffice.org Calc Сервис> Управление расширениями…, затем щелкните на кнопку Добавить (рис. П. 1.1), и отыщите в вашей файловой системе файл scsolver.uno.oxt (рис. П. 1.2). Нажатие на кнопку. Открыть приведет к автоматической установке расширения. Однако для того, чтоб начать его использовать, нужно закрыть и снова запустить OpenOffice.org Calc.

Рис. П. 1.1

Пусть значения хранятся в ячейках A1: A4. А значение функции L в ячейке С1. Введем ограничения:

С2 =-5*A1-A2+2*A3.

С3=-А1+А3+А4.

С4=-3*А1+5*А4.

Рис. П. 1.2

Таким образом, мы задали условие исходной задачи линейного программирования.

Выполним команду из главного меню Сервис>Поиск решения, появится окно Оптимальное решение, представленное на рис. П. 1.3.

Рис. П. 1.3

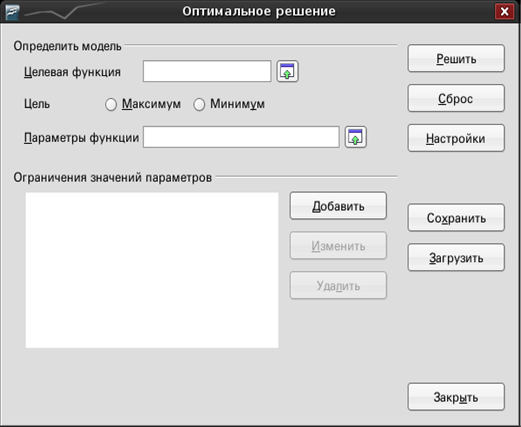
Устремим целевую функцию в ячейке C1 к минимуму. Для этого введем в поле Целевая функция введем ячейку С1 и установим опцию Минимум. В поле Параметры функции необходимо указать адреса ячеек, в которых хранятся изменяемые значения. В нашем случае это ячейки А1: А4.

Для добавления ограничений необходимо щелкнуть по кнопке Добавить, появится диалоговое окно Ограничение (рис. П. 1.4). В поле ввода Ячейка необходимо ввести адрес ячейки, где хранится ограничение, затем, щелкнув по стрелке, выбрать знак и ввести конкретное значение ограничения в поле Ограничение. Щелчок по кнопке OK означает ввод очередного ограничения и возврат к диалоговому окну Оптимальное решение.

Рис. П. 1.4

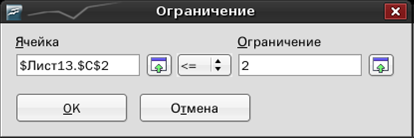
В нашем случае окно будет иметь вид, изображенный на рис. П. 1.5. Щелчок по кнопке. Решить начнет процесс решения задачи, который завершится появлением системного диалогового окна, сообщающего, что решение найдено.

Рис. П. 1.5

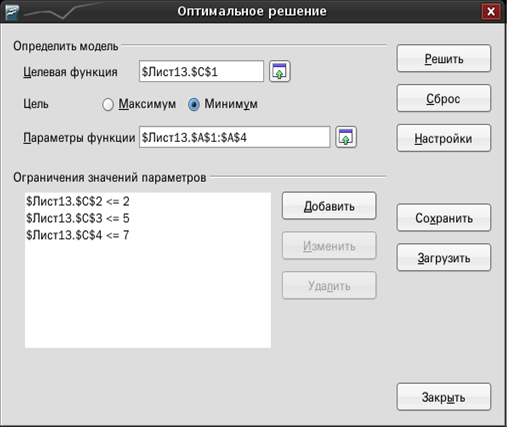
Щелчок по кнопке OK приведет к появлению в ячейке С1 значения целевой функции L, а в ячейках A1: A4 — значений переменных, при которых целевая функция достигает минимального значения.

Итак, назначение основных кнопок и окон диалогового окна Оптимальное решение:

Поле Целевая функция — определяет целевую ячейку, значение которой необходимо максимизировать или минимизировать, или сделать равным конкретному значению.

Опции Максимум и Минимум определяют, что необходимо сделать со значением целевой ячейки — максимизировать, минимизировать или сделать равным конкретному значению.

Поле Параметры функции определяет изменяемые ячейки. Изменяемая ячейка — это ячейка, которая может быть изменена в процессе поиска решения для достижения нужного результата.

Окно Ограничения значений параметров перечисляет текущие ограничения в данной задаче. Ограничение есть условие, которое должно удовлетворяться решением; ограничения перечисляются в виде ячеек или интервалов ячеек, обычно содержащих формулу, которая зависит от одной или нескольких изменяемых ячеек, чье значение должно попадать внутрь определенных границ или удовлетворять равенству.

Кнопки Добавить, Изменить, Удалить позволяют добавить, изменить или удалить ограничение. линейное программирование задача модель Кнопка Решить запускает процесс решения определенной задачи.

Кнопка Закрыть закрывает окно диалога Оптимальное решение, не решая проблемы.

Кнопка Сброс очищает все текущие установки задачи и возвращает все параметры к их значениям по умолчанию.

Кнопка Настройки выводит окно диалога, в котором можно контролировать различные аспекты процесса отыскания решения (рис. П. 1.6).

Рис. П. 1.6

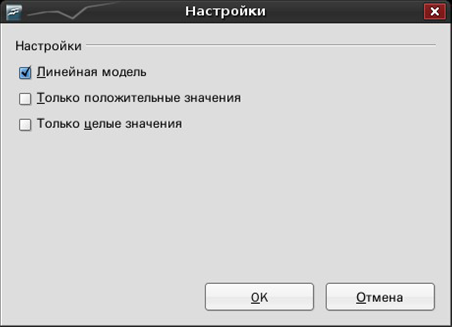
С помощью решающего блока можно решить множество различный оптимизационных задач (задач на максимум и минимум) с ограничениями любого типа. При решении задачи целочисленного программирования необходимо добавить ограничение, показывающее, что переменные целочисленные. При решении других оптимизационных задач вводят целевую функцию и ограничения.

Задачи.

1. Найти экстремум функции.

.

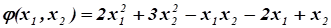
Решение.

Необходимые условия экстремума:

.

.

Из системы уравнений Находим.

.

Достаточные условия экстремума:

.

.

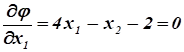
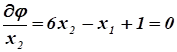
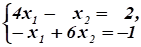
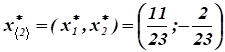
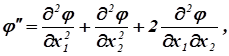
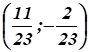
Следовательно, в точке функция имеет минимум:

.

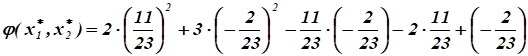
2. Для изготовления 2-х видов продукции используются 3 типа ресурсов.

Запасы ресурсов и их расход на изготовление продукции, а также прибыль, получаемая от реализации одной единицы продукции, приведены в таблице:

Требуется построить математическую модель задачи линейного программирования для составления такого плана производства продукции, при котором прибыль от ее реализации будет максимальной и найти ее решение в пакете Excel (смотри задачу № 1).

Решение.

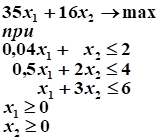
3. По данным отчетного периода получен следующий баланс трехотраслевой экономической системы:

Определить валовый выпуск отраслей, обеспечивающий новый конечный продукт .

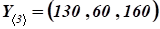
Решение.

Расчет коэффициентов прямых затрат:

.

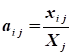
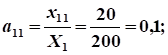
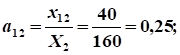
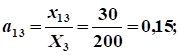
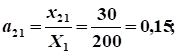
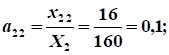
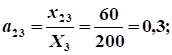
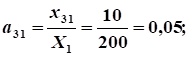
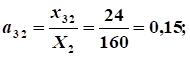
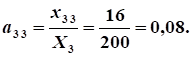
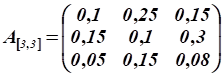
Расчет коэффициентов полных затрат:

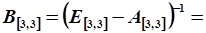
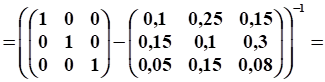
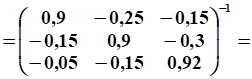
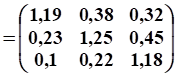
Обратная матрица рассчитана на ПК с помощью Excel.

Определение валового выпуска отраслей:

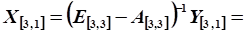
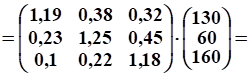
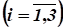
4. Для реконструкции трех заводов выделено 5 млн руб. капиталовложений. Увеличение выпуска продукции (в млн. руб.) после реконструкции в зависимости от выделенногоому заводу объема капиталовложений обозначим и зададим в таблице:

Необходимо найти вариант распределения капиталовложений, при котором суммарное увеличение выпуска продукции на трех заводах максимально.

Решение.

Сначала (прямой прогон) рассчитаем функции, показывающие суммарное увеличение выпуска продукции на заводах, по рекуррентному соотношению:

.

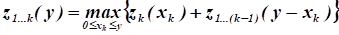
Для, т. е. при выделении объема капиталовложений одному заводу (например, первому) функция совпадает с .

Рассчитаем функцию :

Рассчитаем функцию, т.к. только при полном выделении капиталовложений всем заводам достигается максимальное суммарное увеличение выпуска ими продукции:

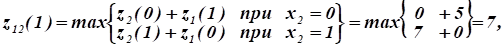
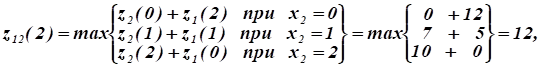
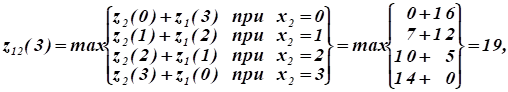
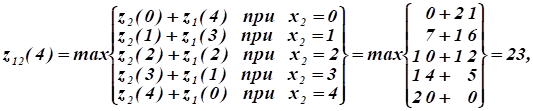
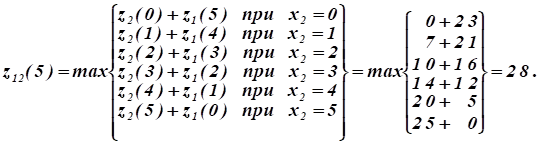
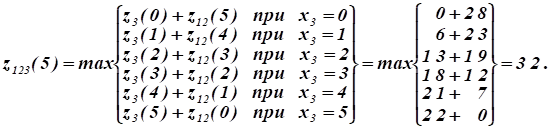
Затем (обратный прогон) находим, что максимальное суммарное увеличение выпуска продукции не трех заводах млн. руб. При этом третьему заводу выделяется 2 млн руб. капиталовложений, а остальным двум — 3 млн руб.

При выделении двум оставшимся заводам 3 млн руб. капиталовложений максимальное суммарное увеличение выпуска продукции на них млн. руб. При этом второму заводу выделяется 1 млн руб. Тогда первому заводу выделяется оставшиеся 2 млн руб. капиталовложений.

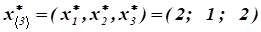
Итак, максимальное суммарное увеличение выпуска продукции на трех заводах 32 млн руб. при оптимальном распределении капиталовложений млн. руб.

5. Найти условный экстремум функции.

при условии (ограничении).

.

Решение.

Составим функцию Лангранжа:

.

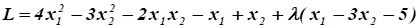
Необходимые условия экстремума:

.

.

.

Из системы уравнений Находим.

.

Достаточные условия экстремума:

Следовательно, в точке.

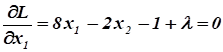
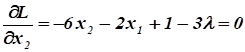
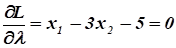
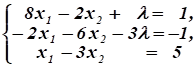
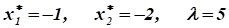
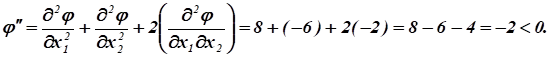
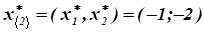
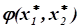
целевая функция имеет максимум:

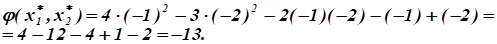
6. Какое должно быть непроизводственное потребление на интервале времени для того, чтобы рост валового продукта определялся зависимостью.

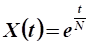
Решение.

Используем уравнение движения:

.

Производная функции валового продукта:

.

Подставим в уравнение движения:

.

Выразим функцию непроизводственного потребления:

Ответ:

• 7. Во сколько раз увеличится непроизводственное потребление в конечный момент времени по сравнению с начальным моментом времени, если рост валового продукта определяется зависимостью
• ?

Решение.

Функция непроизводственного потребления при :

Функция непроизводственного потребления при :

Тогда:

Ответ:

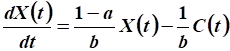
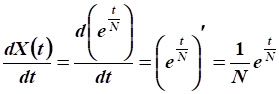
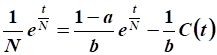
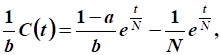
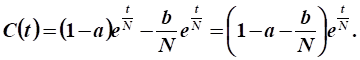
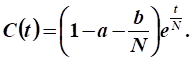
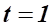
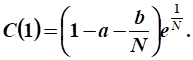
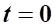
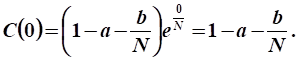
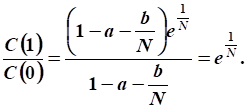
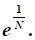
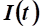
8. Какие нужны капитальные вложения на интервале времени для того, чтобы воспроизводство основных производственных фондов (ОПФ) определялось зависимостью.

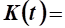
Решение.

Используем уравнение движения:

.

Производная функции ОПФ:

.

Подставим в уравнение движения:

.

Выразим функцию валовых капитальных вложений:

Ответ:

9. Рассчитайте значение целевого функционала, определяющего качество изменения ОПФ на интервале времени, при найденной в задаче 3 функции .

Решение.

Ответ:

• 10. Во сколько раз нужно увеличить капитальные вложения в конечный момент времени по сравнению с начальным моментом времени для того, чтобы воспроизводство основных производственных фондов (ОПФ) определялось зависимостью
• ?

Решение.

Функция валовых капитальных вложений (см. задачу 3) при :

Функция валовых капитальных вложений (см. задачу 3) при :

Тогда:

Ответ:

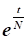
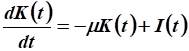
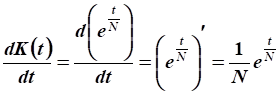
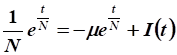
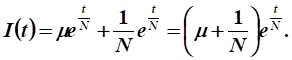
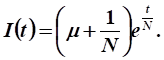
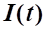
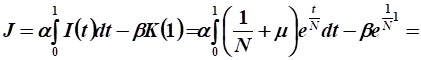
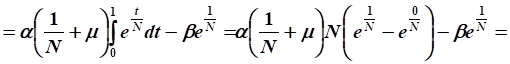
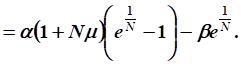
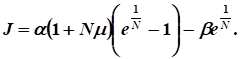
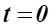
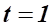
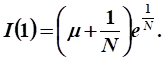
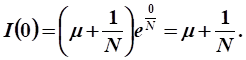
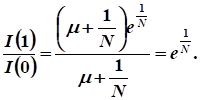
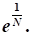
11. Рассчитать значение целевого функционала в задаче оптимального управления развитием экономики на интервале управления при.

.

Решение.

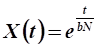
Используем уравнение движения:

.

Производная функции валового продукта:

.

Подставим в уравнение движения:

.

Выразим функцию непроизводственного потребления:

Расчет значения целевого функционала:

Ответ:

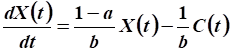
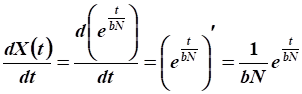
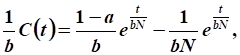
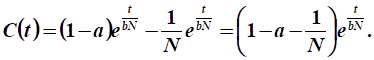
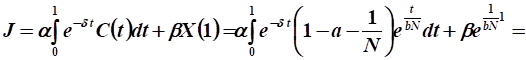
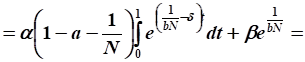
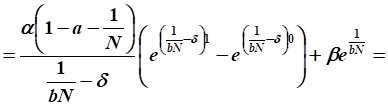
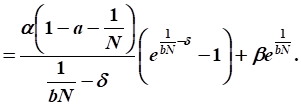
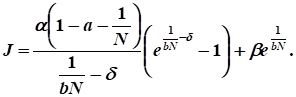
12. Рассчитать значение целевого функционала в задаче оптимального управления распределением капитальных вложений на интервале управления.

при .

Решение.

Используем уравнение движения:

.

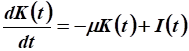
Производная функции основных производственных фондов (ОПФ):

.

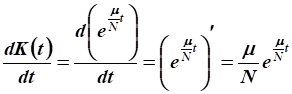
Подставим в уравнение движения:

.

Выразим функцию валовых капитальных вложений:

Расчет значения целевого функционала:

Ответ:

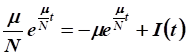
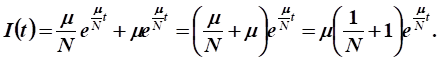
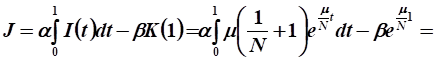
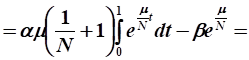
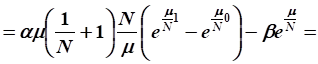
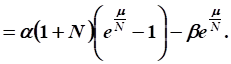
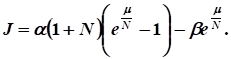
13. Для роста валового продукта, определяемого зависимостью, рассчитано, что непроизводственное потребление, т. е. управление в задаче оптимального управления развитием экономики, должно быть.

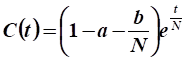
Требуется определить, во сколько раз нужно увеличить непроизводственное потребление, т. е. изменить управление в задаче оптимального управления развитием экономики, для того, чтобы рост валового продукта увеличился в раз.

Решение.

При росте валового продукта в раз функция валового продукта будет иметь вид:

Используем уравнение движения:

.

Производная функции валового продукта:

.

Подставим в уравнение движения:

.

Выразим функцию непроизводственного потребления:

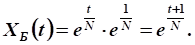
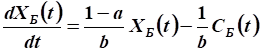
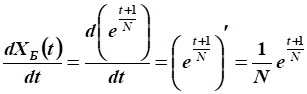
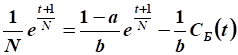
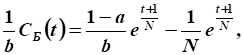
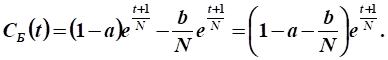
Нужно увеличить непроизводственное потребление в такое количество раз:

Ответ:

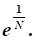
14. Во сколько раз нужно уменьшить валовые капитальные вложения (инвестиции) для того, чтобы основные производственные фонды уменьшились с.

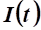
до.

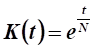
в задаче оптимального управления распределением капитальных вложений?

Решение.

При функция валовых капитальных вложений (см. задачу 3).

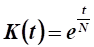
При функция валовых капитальных вложений определяется следующим образом.

Используем уравнение движения:

.

Производная функции ОПФ:

Подставим в уравнение движения:

.

Выразим функцию валовых капитальных вложений:

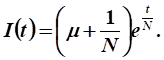
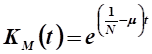
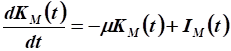
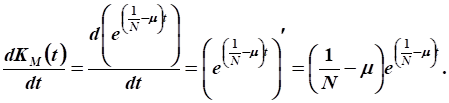
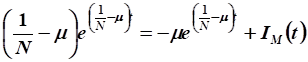
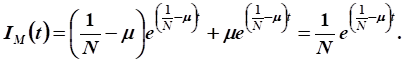
Нужно уменьшить валовые капитальные вложения в такое количество раз:

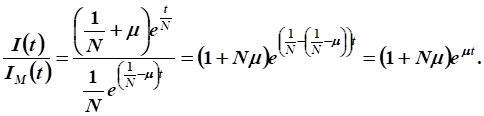
Ответ: