Геометрический смысл производной

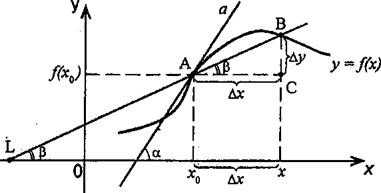
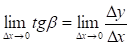Рассмотрим график функции у = f (х), дифференцируемой в окрестностях точки x0.

Рассмотрим произвольную прямую, проходящую через точку графика функции — точку А (x0, f (х0)) и пересекающую график в некоторой точке B (x;f (x)). Такая прямая (АВ) называется секущей. Из? АВС: АС = ?x; ВС =?у; tgв=?y/?x .

Так как АС || Ox, то ALO = BAC = в (как соответственные при параллельных). Но ALO — это угол наклона секущей АВ к положительному направлению оси Ох. Значит, tgв = k — угловой коэффициент прямой АВ.

Теперь будем уменьшать? х, т. е. ?х> 0. При этом точка В будет приближаться к точке, А по графику, а секущая АВ будет поворачиваться. Предельным положением секущей АВ при? х> 0 будет прямая (a), называемая касательной к графику функции у = f (х) в точке А.

Если перейти к пределу при? х > 0 в равенстве tgв =?y/?x, то получим или tg =f '(x0), так какугол наклона касательной к положительному направлению оси Ох, по определению производной. Но tg = k — угловой коэффициент касательной, значит, k = tg = f '(x0).

Итак, геометрический смысл производной заключается в следующем:

Производная функции в точке x0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x0.