Алгоритм решения системы методом Гаусса

Процесс решения по методу Гаусса состоит из двух этапов: прямой и обратный ходы.

Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных — обратным. Если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Тем не менее, для нормальной матрицы с ненулевым определителем всегда возможна такая перестановка уравнений, что на главной диагонали не будет нулей. В приведенном коде для простоты перестановок не делается, зато делается проверка решения, а прямой и обратный ход для наглядности вынесены в отдельные подпрограммы.

На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним.

После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.

На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.

Если в процессе приведения системы к ступенчатому виду появятся нулевые уравнения, т. е. равенства вида 0=0, их отбрасывают. Если же появится уравнение вида то это свидетельствует о несовместности системы.

На этом прямой ход метода Гаусса заканчивается.

Алгоритм прямого прохода:

Выбрать максимальный элемент строки стоящий справа от текущего диагонального элемента, запомнить столбец, в котором он стоит;

Если максимальный элемент равен нулю, то СЛАУ не имеет решения, т.к. в системе присутствую линейно зависимые уравнения;

Поменять столбец найденный в пункте 1, со столбцом, в котором располагается текущий диагональный элемент;

Разделить все элементы строки на текущий диагональный элемент (он изменился, т.к. столбцы были переставлены);

Вычитаем текущую строку из ниже лежащих строк матрицы, умножая ее на коэффициент при соответствующем неизвестном.

Прямой проход завершен, результат — нижняя (находящаяся под главной диагональю) треугольная матрица заполнена нулями.

На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений.

Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (она в нем всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх.

Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.

Примечание: на практике удобнее работать не с системой, а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент a₁₁ был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на a₁₁).

Запишем систему Ax=f, в развернутом виде.

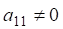
Предположим, что. Последовательно умножая первое уравнение на и складывая с i-м уравнение, исключим из всех уравнений кроме первого. Получим систему.

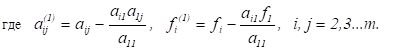
Аналогичным образом из полученной системы исключим. Последовательно, исключая все неизвестные, получим систему треугольного вида.

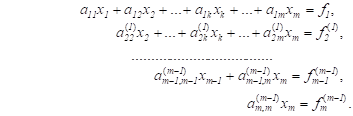
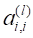
Описанная процедура называется прямым ходом метода Гаусса. Заметим, что ее выполнение было возможно при условии, что все, не равны нулю.

Выполняя последовательные подстановки в последней системе, (начиная с последнего уравнения) можно получить все значения неизвестных.

.

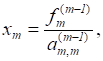
Эта процедура получила название обратный ход метода Гаусса.