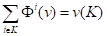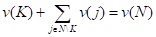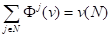Вектор Шепли произвольных игр
Для любой перестановки множества N (аксиома анонимности); Лемма. Возможно задание вектора Шепли двумя свойствами: Для любого автоморфизма игры (аксиома симметрии); Означающее, что выполнено утверждение аксиомы 1. Для любых двух игр
Вектор Шепли произвольных игр (реферат, курсовая, диплом, контрольная)
Ответ: Определение. Вектором Шепли называется отображение, которое каждой игре в форме характеристической функции ставит в соответствие дележ в соответствующей игре, если оно удовлетворяет следующим условиям:
- 1. для любого носителя K (аксиома эффективности);
- 2. для любого автоморфизма игры (аксиома симметрии);
- 3. для любых двух игр <N, v> и <N, v> (аксиома агрегации).
Лемма. Вместо аксиомы эффективности можно использовать следующее свойство.
4. для любого болвана i (аксиома болвана).
Доказательство. Пусть выполнены аксиомы 1,2,3. Рассмотрим произвольного болвана i. Множество N{i} является носителем, поэтому.
.
Так как игрок i является болваном.
v(N{i})+v(i)=v(N).
А так как вектор (v) является дележом в игре <N, v> выполняется условие.
.
Сравнивая три полученных равенства, получим, то есть выполняется аксиома 4.
Обратно, пусть выполняются аксиомы 2, 3 и 4. Рассмотрим произвольный носитель K. Так как все игроки, не входящие в K являются болванами, выполняется условие.
.
По аксиоме болвана v(j)=j(j) для jNK. А так как вектор (v) является дележом в игре <N, v> выполняется условие.
.
Из этих трех условий получаем равенство.
.
означающее, что выполнено утверждение аксиомы 1.
Лемма. Возможно задание вектора Шепли двумя свойствами:
- 1) для любой перестановки множества N (аксиома анонимности);
- 2) если для всех коалиций K не содержащих игрока i, то i(v)= i(w) (аксиома маргинальности).