Построение сетевого графика проекта

Для схематичного отражения взаимозависимости и последовательности работ в практике проектного управления применяется сетевое планирование, компонентом которого является сетевой график, представляющий собой расписание последовательности выполнения и взаимосвязи работ [7].

Для составления сетевого графика необходимо проанализировать последовательность и взаимозависимость работ, так как имеется 2 возможных исполнителя и некоторые работы могут вестись параллельно.

Временные параметры сетевого графика рассчитываются по определенным правилам.

Общая продолжительность проекта является важным фактором при управлении проектами, требующими проведения большого количества мероприятий. Общую продолжительность можно рассчитать по сетевому графику при условии, что известна продолжительность каждого мероприятия, требуемого в соответствии с проектом.

Резерв времени — это количественный показатель подвижности определенного действия при условии обязательного завершения проекта в минимально возможные сроки. Суммарный, свободный и независимый резервы времени показывают величину подвижности определенного действия исходя из своего воздействия на предыдущие и последующие действия.

На основе данных о перечне и продолжительности работ построили трехфакторную модель сетевого графика и рассчитали его временные параметры (рисунок 3).

Существует большое количество алгоритмов расчета сетевых графиков, как ручным, так и автоматическим способом. Знание «ручных» технологий позволяет лучше понять взаимосвязь между этими показателями и использовать сетевые модели без каких-либо специализированных программ. [29].

Рассчитаем параметры сетевой модели табличным методом PERT, который является мощным инструментом управления, использование которого помогает существенно снизить неопределенность при планировании проекта. (Таблица 2).

Таблица 2 Расчет аналитических параметров сетевого графика.

h-i.	i.	j.
;
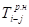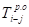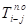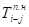;										45−6=39.
-«;
										45−14=31.
-«;
										45−23=22.
-«;
		;		;			;		;	;

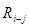
При расчете сетевых моделей методом PERT продолжительность работ является случайной величиной, подчиняющейся собственному закону распределения, а значит, обладающей собственными числовыми характеристиками. Такими характеристиками являются средняя продолжительность работы и дисперсия оценки продолжительности работы (дисперсия работы). [29].

Значения и рассчитываются при допущении, что распределение продолжительностей работ обладает тремя свойствами:

• — Непрерывностью;
• — Унимодальностью (наличием единственного максимума у кривой распределения);
• — Конечностью и неотрицательностью диапазона возможных значений продолжительности (кривая распределения имеет две точки пересечения с осью ОХ, абсциссы которых неотрицательны).

Исходными данными для расчетов служат экспертные оценки продолжительностей работ:

• — Оптимистическая оценка, то есть оценка продолжительности работы i-j при благоприятных условиях;
• — Пессимистическая оценка, то есть оценка продолжительности работы i-j при неблагоприятных условиях;
• — Наиболее вероятная оценка, то есть оценка продолжительности работы i-j при нормальных условиях.

— Средняя продолжительность и дисперсия оценки продолжительности каждой отдельной работы определяются по следующим формулам:

;

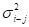
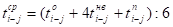
Рассчитаем среднюю продолжительность каждой из работ. (Таблица 3). Для этого проставим пессимистическую и наиболее вероятную продолжительность работ, а за оптимистическое значение продолжительности работ возьмем наши данные (продолжительности выполнения работ по графику).

Таблица 3 Средняя продолжительность работ.

Рассчитаем средние продолжительности работ по формуле.

.

Аналогично рассчитываются средние продолжительности остальных работ.

Рассчитаем дисперсии оценки продолжительности работ по формуле Аналогично рассчитываются дисперсии для остальных работ.

Вероятностные характеристики продолжительности отдельных видов работ используются для определения параметров всего проекта в целом. Когда средняя продолжительность каждой работы определена, продолжительность проекта рассчитывается с помощью уже известных алгоритмов, только при этом в качестве продолжительности работ используется средняя продолжительность. Значения всех аналитических параметров сетевого графика — длины критического пути, определяющего продолжительность всего проекта, и ранних и поздних свершений событий, резервов событий и работ — будут такими же, как если бы мы использовали не среднюю, а обыкновенную продолжительность работ. Но при этом необходимо понимать, что по своей сути все параметры будут являться средними значениями соответствующих случайных величин.

Обобщенной вероятностной оценкой продолжительности всего проекта является средняя длина критического пути сетевого графика, которая вычисляется как сумма всех средних продолжительностей работ, лежащих на критическом пути.

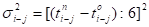
Ожидаемая продолжительность выполнения проекта (средняя продолжительность критического пути сетевого графика проекта) может оказаться неприемлемой. Тогда вместо нее выбирается директивная продолжительность и возникает необходимость оценить вероятность того, что проект завершится не позднее директивно установленного срока.

Для решения нашей задачи необходимо:

— Определить среднее квадратическое отклонение длины критического пути.

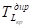
где — дисперсия работы, лежащей на критическом пути.

— Рассчитать аргумент функции Лапласа (интеграла вероятностей) Z.

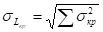
— Найти значение функции Лапласа Ф (Z) (по таблицам стандартного нормального распределения (таблицам интеграла вероятностей)).

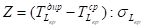
— Вычислить вероятность соблюдения директивных сроков выполнения проекта. 42].

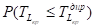
Рассчитаем сетевой график методом PERT. Критический путь этого сетевого графика составляют работы 0−1, 1−2, 2−4, 4−5, 5−7, 7−8, 8−10, 10−11, 11−12, 12−13. Дисперсии работ, составляющих критический путь, следующие:

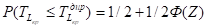
Оценим вероятность выполнения проекта в срок при, равном 45 дней.

Найдем среднее квадратическое отклонение длины критического пути:

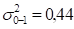
Рассчитаем среднюю длину критического пути:

Рассчитаем значение аргумента функции Лапласа:

Z = (45−57.50)/1.36 = - 9.16.

Определим Ф (Z) с помощью функции MS Excel НОРМСТРАСП ().

Ф (Z) = Ф (-9,16) = 2,59.

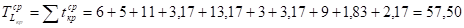
Рассчитаем вероятность = -0,5+0,5*2,59=0,80.

Таким образом, вероятность того, что проект, сетевой график которого представлен на рис. 3, с учетом введенных значений дисперсий критических работ завершится не позднее 45 дней, составляет около 80%.

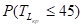
В практике управления проектами возникает необходимость решения и обратной задачи, то есть определения максимального срока выполнения проекта с заданной вероятностью (с заданной надежностью). Продолжительность выполнения проекта при таких условиях может быть найдена следующим образом:

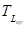
(19).

где — аргумент функции Лапласа, соответствующий значению функции, равному, то есть .

Рассчитаем возможный срок выполнения проекта, сетевой график которого представлен на рис. 3, с заданной надежностью = 0,95.

Найдем аргумент функции Лапласа, соответствующий значения 0,95 (можно воспользоваться таблицей стандартного нормального распределения или же формулой НОРМСТОРБ () в программе MS Excel. Он равен — 1,6449.

По формуле определяем.

= 57,50+1,6449*1,36=59,74 дней.

При заданной вероятности наш проект завершится за 60 дней.