Ядро сечения при внецентренном сжатии

Ядро сечения при внецентренном сжатии

При конструировании стержней из материалов, плохо сопротивляющихся растяжению (бетон), весьма желательно добиться того, чтобы все сечение работало лишь на сжатие. Этого можно достигнуть, не давая точке приложения силы Р слишком далеко отходить от центра тяжести сечения, ограничивая величину эксцентриситета.

Конструктору желательно заранее знать, какой эксцентриситет при выбранном типе сечения можно допустить, не рискуя вызвать в сечениях стержня напряжений разных знаков. Здесь вводится понятие о так называемом ядре сечения. Этим термином обозначается некоторая область вокруг центра тяжести сечения, внутри которой можно располагать точку приложения силы Р, не вызывая в сечении напряжений разного знака.

Пока точка, А располагается внутри ядра, нейтральная ось не пересекает контура сечения, все оно лежит по одну сторону от нейтральной оси и, стало быть, работает лишь на сжатие. При удалении точки, А от центра тяжести сечения нейтральная ось будет приближаться к контуру; граница ядра определится тем, что при расположении точки, А на этой границе нейтральная ось подойдет вплотную к сечению, коснется его.

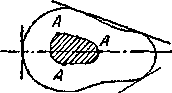
Рис. 1. Комбинации положения сжимающей силы и нейтральной линии

Таким образом, если мы будем перемещать точку, А так, чтобы нейтральная ось катилась по контуру сечения, не пересекая его, то точка, А обойдет по границе ядра сечения. Если контур сечения имеет «впадины», то нейтральная ось будет катиться по огибающей контура.

Чтобы получить очертание ядра, необходимо дать нейтральной оси несколько положений, касательных к контуру сечения, определить для этих положений отрезки и и вычислить координаты и точки приложения силы по формулам, вытекающим из известных зависимостей:

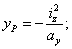
это и будут координаты точек контура ядра и .

При многоугольной форме контура сечения (Рис.2), совмещая последовательно нейтральную ось с каждой из сторон многоугольника, мы по отрезкам и определим координаты и точек границы ядра, соответствующих этим сторонам.

При переходе от одной стороны контура сечения к другой нейтральная ось будет вращаться вокруг вершины, разделяющей эти стороны; точка приложения силы будет перемещаться по границе ядра между полученными уже точками. Установим, как должна перемещаться сила Р, чтобы нейтральная ось проходила все время через одну и ту же точку В (,) — вращалась бы около нее. Подставляя координаты этой точки нейтральной оси в известное уравнение нейтральной оси (линии), получим.

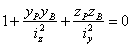
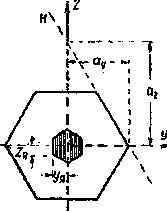
Рис. 2. Ядро сечения для многоугольной формы поперечного сечения

Таким образом координаты и точки приложения силы Р связаны линейно. При вращении нейтральной оси около постоянной точки В точка, А приложения силы движется по прямой. Обратно, перемещение силы Р по прямой связано с вращением нейтральной оси около постоянной точки.

На Рис. 3 изображены три положения точки приложения силы на этой прямой и соответственно три положения нейтральной оси.

Таким образом, при многоугольной форме контура сечения очертание ядра между точками, соответствующими сторонам многоугольника, будет состоять из отрезков прямых линий.

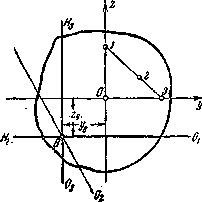
Рис. 3. Динамика построения ядра сечения

стержень растяжение ядро сечение Если контур сечения целиком или частично ограничен кривыми линиями, то построение границы ядра можно вести по точкам.

Рассмотрим несколько простых примеров построения ядра сечения. При выполнении этого построения для прямоугольного поперечного сечения воспользуемся полученными формулами.

Для определения границ ядра сечения при движении точки, А по оси Оу найдем то значение, при котором нейтральная ось займет положение Н1О1. Имеем:

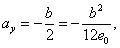
откуда.

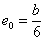
Таким образом, границы ядра по оси Оу будут отстоять от центра сечения на 1/6 величины b (Рис. 4, точки 1 и 3); по оси Oz границы ядра определятся расстояниями (точки 2 и 4).

Для получения очертания ядра целиком изобразим положения нейтральной оси и, соответствующие граничным точкам 1 и 2.

При перемещении силы из точки 1 в точку 2 по границе ядра нейтральная ось должна перейти из положения в положение, все время касаясь сечения, т. е. поворачиваясь вокруг точки D.

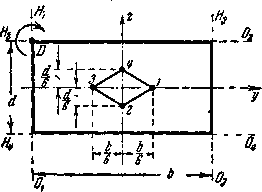
Рис. 4. построение ядра для прямоугольного сечения

Для этого сила должна двигаться по прямой 1 — 2. Точно так же можно доказать, что остальными границами ядра будут линии 2 — 3, 3 — 4 и 4 — 1.

Таким образом, для прямоугольного сечения ядро будет ромбом с диагоналями, равными одной трети соответствующей стороны сечения. Поэтому прямоугольное сечение при расположении силы по главной оси работает на напряжения одного знака, если точка приложения силы не выходит за пределы средней трети стороны сечения.

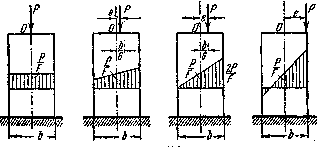
Рис. 5. Динамика изменения напряжений при изменении эксцентриситета

Эпюры распределения нормальных напряжений по прямоугольному сечению при эксцентриситете, равном нулю, меньшем, равном и большем одной шестой ширины сечения, изображены на Рис. 5.

Отметим, что при всех положениях силы Р напряжение в центре тяжести сечения (точка О) одинаково и равно и что сила Р не имеет эксцентриситета по второй главной оси.

Для круглого сечения радиуса r очертание ядра будет по симметрии кругом радиуса. Возьмем какое-либо положение нейтральной оси, касательное к контуру. Ось Оу расположим перпендикулярно к этой касательной. Тогда.

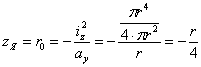
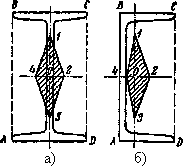
Рис. 6. Ядро сечения для двутавра — а) и швеллера — б)

Таким образом, ядро представляет собой круг с радиусом, вчетверо меньшим, чем радиус сечения.

Для двутавра нейтральная ось при обходе контура не будет пересекать площади поперечного сечения, если будет касаться прямоугольного контура ABCD, описанного около двутавра (Рис.6а). Следовательно, очертание ядра для двутавра имеет форму ромба, как и для прямоугольника, но с другими размерами.

Для швеллера, как и для двутавра, точки 1, 2, 3, 4 контура ядра (Рис. 6 б) соответствуют совпадению нейтральной оси со сторонами прямоугольника ABCD.