Расчет теплообменных аппаратов

Целью теплового расчета является определение поверхности теплообмена, а если последняя известна, то целью расчета является определение конечных температур рабочих жидкостей. Основными расчетными уравнениями теплообмена при стационарном режиме являются уравнение теплопередачи и уравнение теплового баланса. Уравнение теплопередачи:

Q = k· F·(t₁ — t₂) ,.

где Q — тепловой поток, Вт,.

k — средний коэффициент теплопередачи, Вт/(м²град), F — поверхность теплообмена в аппарате, м², t₁ и t₂ — соответственно температуры горячего и холодного теплоносителей.

Уравнение теплового баланса при условии отсутствия тепловых потерь и фазовых переходов:

Q = = m₁ · Dt₁ = m₂· Dt₂ ,.

или.

Q = V₁ r₁· c_р1·(t^/₁ — t^//₁) = V₂ r₂· c_р2 · (t^//₂ — t^/₂), (12.16).

где V1 r1, V2 r2 — массовые расходы теплоносителей, кг/сек, с.

c_р1 и c_р2 — средние массовые теплоемкости жидкостей в интервале температур от t^ґ до t^//,.

t^/₁ и t^//₁ температуры жидкостей при входе в аппарат;

t^/₂ и t^//₂ — температуры жидкостей при выходе из аппарата.

Величину произведения.

V· r·c_р = W, Вт/град называют водяным, или условным, эквивалентом.

С учетом последнего уравнение теплового баланса может быть представлено в следующем виде:

(t^/₁ — t^//₁) / (t^//₂ — t^ґ₂) = W₂ / W₁, (12.17).

W₂, W₁ — условные эквиваленты горячей и холодной жидкостей.

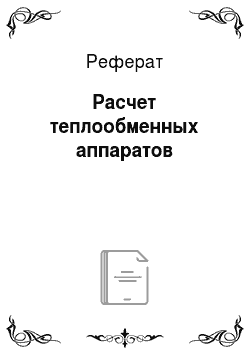
При прохождении через теплообменный аппарат рабочих жидкостей изменяются температуры горячих и холодных жидкостей. На изменение температур большое влияние оказывают схема движения жидкостей и величины условных эквивалентов. На рис. 12.4 представлены температурные графики для аппаратов с прямотоков, а на рис. 12.5 для аппаратов с противотоком.

Как видно из рис. 12.4, при прямотоке конечная температура холодного теплоносителя всегда ниже конечной температуры горячего теплоносителя. При противотоке (рис. 12.5) конечная температура холодной жидкости может быть значительно выше конечной температуры горячей жидкости. Следовательно, в аппаратах с противотоком можно нагреть холодную среду, при одинаковых начальных условиях, до более высокой температуры, чем в аппаратах с прямотоком. Кроме того, как видно из рисунков, наряду с изменениями температур изменяется также и разность температуря между рабочими жидкостями, или температурный напор Dt.

Величины Dt и k можно принять постоянными только в пределах элементарной поверхности теплообмена dF. Поэтому уравнение теплопередачи для элемента поверхности теплообмена dF справедливо лишь в дифференциальной форме:

dQ = k· dF·Dt. (12.18).

Тепловой поток, переданный через всю поверхность F при постоянном среднем коэффициенте теплопередачи k, определяется интегрированием уравнения (12.):

Q = т k· dF·Dt= k· F·Dt_ср, (12.19).

где Dtср — средний логарифмический температурный напор по всей поверхности нагрева.

Для случаев, когда коэффициент теплопередачи на отдельных участках поверхности теплообмена значительно изменяется, его усредняют:

k_ср = (F₁· k₁ + F₂· k₂ + … + F_n· k_n) / (F₁ + F₂ + … + F_n).

Тогда при k_ср = const уравнение (12.9) примет вид.

Q = тk_ср Dt · dF = k_ср · Dt_ср · F. (12.20).

Если температура теплоносителей изменяется по закону прямой линии (рис. 12.6, пунктирные линии), то средний температурный напор в аппарате равен разности среднеарифметических величин:

Dt_ср = (t^/₁ + t^//₁)/2 — (t^//₂ + t^/₂)/2. (12.21).

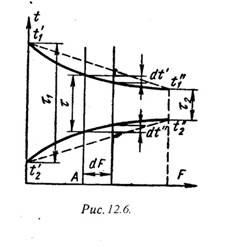
Однако температуры рабочих жидкостей меняются по криволинейному закону. Поэтому уравнение (12.21) будет только приближенным и может применяться при небольших изменениях температуры обеих жидкостей. При криволинейном изменении температуры величину Dt_ср называют среднелогарифмическим температурным напором и определяется по формулам:

для аппаратов с прямотоком.

Dt_ср = [(t^/₁ — t^/₂) — (t^//₁ — t^//₂)] / ln[(t^/₁ — t^/₂)/(t^//₁ — t^//₂)]. (12.22).

для аппаратов с противотоком.

Dt_ср = [(t^/₁ — t^//₂) — (t^//₁ — t^/₂)] / ln[(t^/₁ — t^//₂)/(t^//₁ — t^/₂)]. (12.23).

Численные значения Dt_ср для аппаратов с противотоком при одинаковых условиях всегда больше Dt_ср для аппаратов с прямотоком, поэтому аппараты с противотоком имеют меньшие размеры.