Особенности исследования временных рядов

Корреляционно-регрессионный анализ можно проводить на основе двух типов исходных данных:

• — данные, характеризующие совокупность различных объектов в определенный момент (период) времени;
• — данные, характеризующие один объект за ряд последовательных моментов (периодов) времени.

Временнуй ряд — это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов.

Изучение причинно-следственных зависимостей показателей, представленных в форме временных рядов имеет свою специфику.

Применение в этих целях традиционных методов корреляционно-регрессионного анализа может привести к ряду проблем. Они связаны со спецификой временных рядов как источника данных для анализа. Каждый уровень временнуго ряда содержит три основные компоненты: тенденцию, циклические или сезонные колебания и случайную компоненту.

Особое значение имеет тенденция. Если рассматриваемые временные ряды имеют тенденцию, коэффициент корреляции по абсолютной величине будет высоким (положительным в случае совпадения или отрицательным в случае противоположной направленности тенденций рядов). Однако из этого еще нельзя делать вывод о том, что имеет место причинно-следственная связь. Высокий коэффициент корреляции в данном случае может быть следствием того, что ряды данных зависят от времени или содержат тенденцию. При этом одинаковую или противоположную тенденцию могут иметь ряды, совершенно не связанные друг с другом причинно-следственной зависимостью. Например, коэффициент корреляции между численностью выпускников вузов и числом домов отдыха в РФ в период 1970;1990 гг. составил 0,8. Это, конечно, не означает, что увеличение количества домов отдыха способствует росту числа выпускников вузов или наоборот.

Чтобы получить коэффициенты корреляции, характеризующие причинно-следственную связь между изучаемыми рядами, следует избавиться от так называемой ложной корреляции, вызванной наличием тенденции в каждом ряде. Наличие тенденции в каждом из анализируемых временных рядов означает, что на зависимую (результирующую) и независимую (факторную) переменные модели оказывает воздействие фактор времени, который непосредственно в корреляционно-регрессионной модели не учтен. Это влияние фактора времени будет выражено в корреляционной зависимости между значениями остатков в модели за текущий и предыдущий моменты времени, которая получила название автокорреляции в остатках.

Обычно устранение ложной корреляции осуществляют методами исключения тенденции, сущность которых заключается в том, чтобы устранить или зафиксировать воздействие фактора времени на формирование уровней ряда.

С целью устранения тенденции можно применять наиболее простой из существующих способов — метод последовательных разностей. Также существуют более сложные методы: метод отклонения от трендов, метод включения в модель регрессии по временным рядам фактора времени и др.

Если временнуй ряд содержит ярко выраженную линейную тенденцию Определить характер тенденции ряда можно воспользовавшись рекомендациями раздела «Построение трендов», ее можно устранить путем замены исходных данных (уровней ряда) цепными абсолютными приростами (разностями).

Если временнуй ряд содержит тенденцию в форме параболы второго порядка, то для ее устранения можно заменить исходные данные (уровни ряда) на вторые разности (разности разностей).

Основными недостатками метода последовательных разностей являются, во-первых, то, что он не всегда обеспечивает высокую точность результатов, особенно при определении уравнения регрессии, и во-вторых, при переходе на абсолютные приросты (разности) и вторые разности уменьшается количество исходных данных (наблюдений) на одно и два соответственно.

Пример.

Вернемся к рассмотренному ранее примеру анализа зависимости объема реализации (спроса) товара от его цены, величины дохода потребителей и объема затрат на маркетинг. В таблице 1.4 были представлены данные об изменении показателей по годам. В них просматривается некоторая тенденция к росту. Для ее устранения в качестве исходной информации для корреляционного анализа перейдем на абсолютные приросты (рис. 1.30). Таким образом, в нашем распоряжении остается восемь наблюдений.

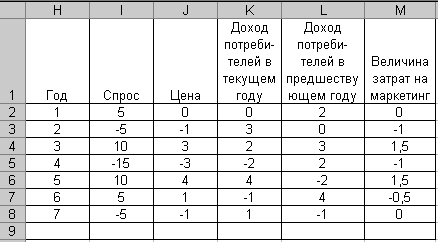
Рисунок 1.30 — Модифицированные исходные данные, введенные в Excel для проведения корреляционного анализа.

Проведенный по уточненным данным анализ дал следующие результаты (рис. 1.31): более четко проявилась связь спроса с ценой (коэффициент корреляции возрос с 0,8 до 0,94) и затратами на маркетинг (корреляции возрос с 0,7 до 0,8); уровень связи с величиной доходов потребителей в текущем году практически не изменился, а с величиной доходов в предшествующем году существенно снизился (до 0,07) — связь этого фактора с уровнем спроса практически отсутствует.

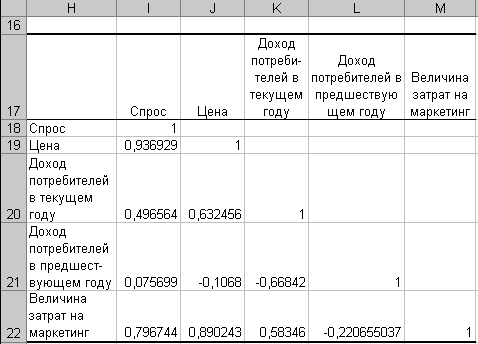
Рисунок 1.31.

Таким образом, гипотезы, выдвинутые по результатам анализа данных первого уровня, в целом подтвердились и приобрели более яркую выраженность.

В практике эконометрических исследований корреляционный анализ является первым этапом, за которым следует регрессионный анализ, позволяющий получить уравнение регрессии (статистическую модель). В совокупности корреляционный и регрессионный анализ являются важным инструментом исследования социально-экономических процессов и явлений.

Например, можно разработать статистическую модель, связывающую показатели роста экономики и показатели (факторы), отображающие результативность работы нефтяного комплекса.

В качестве показателей, оценивающих нефтяной комплекс, могут быть отобраны: внутренний валовой продукт в году (y₁); величина промышленного производства в год (y₂); выручка от экспорта в год (y₃).

В качестве показателей, отражающих результаты работы нефтяного комплекса страны, можно взять: объем добычи нефти в год (x₁); инвестиции в основной капитал нефтяных компаний в год (x₂); выручка от экспорта нефти и нефтепродуктов в год (x₃); эксплуатационный фонд скважин в год (x₄); величина потребления нефти в РФ в год (x₅).

В этом случае корреляционный анализ данных показал высокую тесноту связи между y₁ и y₂ (r_y1y2=0,86), y₃ и y₂ (r_y3y2=0,7), а также между x₁ и x₅ (r_x1x5=0,96), x₂ и x₄ (r_x2x4=0,78), поэтому для дальнейшего анализа следует оставить y₁, x₂ и x₃.

В результате проведенного регрессионного анализа получено уравнение множественной регрессии следующего вида:

.

Уравнение характеризуется коэффициентом множественной корреляции R=0,997 и критерием Фишера (F) (критерий уровня значимости) F = 734,451 при критическом значении F_кр = 5,987. На основе этого можно сделать вывод о том, что уравнение регрессии значимо и имеется сильная связь между признаками.