Методика изучения квадратных уравнений

Обучение решению уравнений начинается с простейших их видов, и программа обусловливает постепенное накопление как их видов, так и «фонда» тождественных и равносильных преобразований, с помощью которых можно привести произвольное уравнение к простейшим. В этом направлении следует строить и процесс формирования обобщенных приемов решения уравнений в школьном курсе алгебры. В курсе математики… Читать ещё >
Методика изучения квадратных уравнений (реферат, курсовая, диплом, контрольная)
С началом изучения систематического курса алгебры основное внимание уделяется способам решения квадратных уравнений, которые становятся специальным объектом изучения. Для этой темы характерна большая глубина изложения и богатство устанавливаемых с ее помощью связей в обучении, логическая обоснованность изложения. Поэтому она занимает исключительное положение в линии уравнений и неравенств. К изучению этой темы учащиеся приступают, уже накопив определенный опыт, владея достаточно большим запасом алгебраических и общематематических представлений, понятий, умений.
Умение решать квадратные уравнения служит базой для решения других уравнений и их систем (дробных рациональных, иррациональных, высших степеней).
Для того чтобы решить любое квадратное уравнение, учащиеся должны знать:
- · формулу нахождения дискриминанта;
- · формулу нахождения корней квадратного уравнения;
- · алгоритмы решения уравнений данного вида.
уметь:
- · решать неполные квадратные уравнения;
- · решать полные квадратные уравнения;
- · решать приведенные квадратные уравнения;
- · находить ошибки в решенных уравнениях и исправлять их;
- · делать проверку.
Решение каждого уравнения складывается из двух основных частей:
- · преобразования данного уравнения к простейшим;
- · решения уравнений по известным правилам, формулам или алгоритмам.
При изучении темы «Квадратные уравнения» рассматриваются неполные, полные и приведенные квадратные уравнения. Для изучения данной темы были проанализированы современные школьные учебники разных авторов, таких как А. Г. Мордкович, С. М. Никольский, Ю. Н. Макарычев, М. И. Башмаков.
Анализ учебников.
А.Г. Мордкович. | С.М. Никольский. | Ю.Н. Макарычев. | М.И. Башмаков. | ||
Историческая справка. | ; | ; | ; | ||
Неполные квадратные уравнения. | |||||
Полные квадратные уравнения. | |||||
Приведённые квадратные уравнения. | |||||
Теорема Виета. | ; | ; | |||
Теорема, обратная теореме Виета. | ; | ; | |||
Исходя из таблицы можно сделать вывод о том, что в учебниках алгебры разных авторов есть сходства и различия. Во всех современных школьных учебниках алгебры методическая линия изучения квадратных уравнений одинакова. В учебнике под ред. М. И. Башмакова дается историческая справка, а в других учебниках этого нет. В учебниках алгебры С. М. Никольского и Ю. Н. Макарычева при изучении темы «Квадратные уравнения» рассматриваются прямая и обратная теорема Виета.
Обучение решению уравнений начинается с простейших их видов, и программа [4,131] обусловливает постепенное накопление как их видов, так и «фонда» тождественных и равносильных преобразований, с помощью которых можно привести произвольное уравнение к простейшим. В этом направлении следует строить и процесс формирования обобщенных приемов решения уравнений в школьном курсе алгебры. В курсе математики старших классов учащиеся сталкиваются с новыми классами уравнений, систем или с углубленным изучением уже известных классов. Однако это мало влияет на уже сформированную систему знаний, умений и навыков; они дополняют ее новым фактическим содержанием.
Обобщение способов деятельности учащихся при решении квадратных уравнений происходит постепенно. Можно выделить следующие этапы при изучении темы «Квадратные уравнения»:
I этап — «Решение неполных квадратных уравнений».
II этап — «Решение полных квадратных уравнений».
III этап — «Решение приведенных квадратных уравнений».
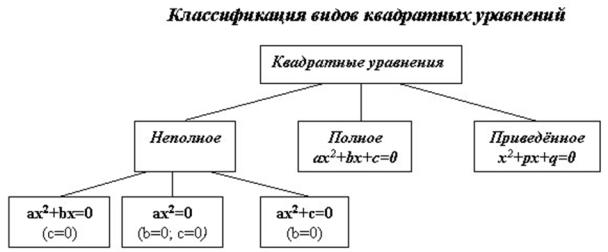
На первом этапе рассматриваются неполные квадратные уравнения. Так как сначала математики научились решать неполные квадратные уравнения, поскольку для этого не пришлось, как говорится, ничего изобретать. Это уравнения вида: ах2 = 0, ах2 + с = 0, где с? 0, ах2 + bх = 0, где b? 0.
Рассмотрим решение несколько таких уравнений:

1. Если ах2 = 0.
Уравнения такого вида решаются по алгоритму:
- 1) найти х2;
- 2) найти х.
Например, 5х2 = 0 .
Разделив обе части уравнения на 5 получается: х2 = 0, откуда х = 0.
2. Если ах2 + с = 0, с? 0.
Уравнения данного вида решаются по алгоритму:
- 1) перенести слагаемые в правую часть;
- 2) найти все числа, квадраты которых равны числу с.
Например, х2 — 5 = 0. Это уравнение равносильно уравнению х2 = 5. Следовательно, надо найти все числа, квадраты которых равны числу 5. Таких чисел только два v5 и — v5. Таким образом, уравнение х2 — 5 = 0 имеет два корня: x1 =v5, x2= - v5 и других корней не имеет.
3. Если ах2 + bх = 0, b? 0.
Уравнения такого вида решаются по алгоритму:
- 1) перенести общий множитель за скобки;
- 2) найти x1, x2.
Например, х2 — 3х = 0. Перепишем уравнение х2 — 3х = 0 в виде х (х — 3) = 0. Это уравнение имеет, очевидно, корни x1 = 0, x2 = 3. Других корней оно не имеет, ибо если в него подставить вместо х любое число, отличное от нуля и 3, то в левой части уравнения.
х (х — 3) = 0 получится число, не равное нулю.
Итак, данные примеры показывают, как решаются неполные квадратные уравнения:
- 1) если уравнение имеет вид ах2 = 0, то оно имеет один корень х = 0;
- 2) если уравнение имеет вид ах2 + bх = 0, то используется метод разложения на множители: х (ах +b) = 0; значит, либо х = 0, либо ах + b = 0. В итоге получается два корня: x1 = 0; x2 = -b/a ;
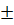
3) если уравнение имеет вид ах2 + с = 0, то его преобразуют к виду ах2 = - с и далее х2.= - c/a. В случае, когдаc/a < 0, уравнение х2 = - c/a не имеет корней (значит, не имеет корней и исходное уравнение ах2 + с = 0). В случае, когда — c/a > 0, т. е. — c/a = m, где m>0, уравнение х2 = m имеет два корня x1 = vm; x2 = -v m (в этом случае допускается более короткая запись x1,2 = vm.
Таким образом, неполное квадратное уравнение может иметь два корня, один корень, ни одного корня.
На втором этапе осуществляется переход к решению полного квадратного уравнения. Это уравнения вида ах2 + bx + c = 0, где a, b, c — заданные числа, а? 0, х — неизвестное.
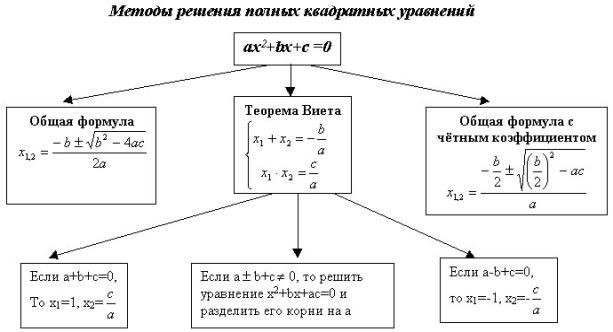
Любое полное квадратное уравнение можно преобразовать к виду ах2 + bx + c = 0, для того, чтобы определять число корней квадратного уравнения и находить эти корни. Рассматриваются следующие случаи решения полных квадратных уравнений: D 0.
1. Если D < 0, то квадратное уравнение ах2 + bx + c = 0 не имеет действительных корней.
Например, 2х2 + 4х + 7 = 0. Решение: здесь, а = 2, b = 4, с = 7.
D = b2 — 4ас = 42 — 4*2*7 = 16 — 56 = - 40.
Так как D < 0, то данное квадратное уравнение не имеет корней.
2. Если D = 0, то квадратное уравнение ах2 + bx + c = 0 имеет один корень, который находится по формуле х= -b/2a.
Например, 4х — 20х + 25 = 0. Решение: а = 4, b = - 20, с = 25.
D = b2 — 4ас = (-20) 2 — 4*4*25 = 400 — 400 = 0.
Так как D = 0, то данное уравнение имеет один корень. Этот корень находится по формуле x=-b/2a. Значит, x=20/4, х=5.
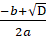
3. Если D > 0, то квадратное уравнение ах2 + bx + c = 0 имеет два корня, которые находятся по формулам: х1 =; х2 =. (1).
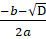
Например, 3х2 +8х — 11 = 0. Решение: а = 3, b = 8, с = -11. D = b2 — 4ас = 82 — 4*3*(-11) = 64 + 132 = 196= 142.
Так как D > 0, то данное квадратное уравнение имеет два корня. Эти корни находятся по формуле:
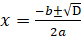

. Значит х1 = (-8−14)/6 = = -3, х2= (-8+ 14)/6=1.
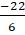
Составляется алгоритм решения уравнения вида ах2 + bx + c = 0.
- 1. Вычислить дискриминант D по формуле D = b2 — 4ас.
- 2. Если D < 0, то квадратное уравнение ах2 + bx + c = 0 не имеет корней.
- 3. Если D = 0, то квадратное уравнение имеет один корень, который находится по формуле
- 4. Если D > 0, то квадратное уравнение ах2 + bx + c = 0 имеет два корня:
х1 =; х2 = .
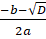
Это алгоритм универсален, он применим как к неполным, так и к полным квадратным уравнениям. Однако неполные квадратные уравнения обычно по этому алгоритму не решают.
Математики — люди практичные, экономные, поэтому пользуются формулой:
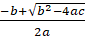
х1 =; х2 =. (2).
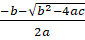
Итак, можно сделать вывод, что квадратные уравнения можно решать подробно, используя сформулированное выше правило; можно — записать сразу формулу (2) и с ее помощью делать необходимые выводы. [1,98].
На третьем этапе рассматриваются приведенные квадратные уравнения, которые имеют вид х2 +px + q = 0 (3), где p и q — данные числа. Число p — коэффициент при х, а q — свободный член. Дискриминант уравнения равен: D = p2 — 4q.
Рассматривают 3 случая:
1. D > 0, тогда уравнение (3) имеет два корня, вычисляемые по формуле.
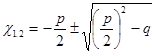
(4).
2. D = 0, тогда уравнение (3) имеет единственный корень, или, как говорят, два совпадающих корня:
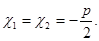
3. D < 0, то уравнение не имеет корней.
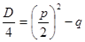
Обычно в случае приведенного квадратного уравнения (3) вместо D рассматривается выражение, имеющее тот же знак, что и D. При этом формулу корней приведенного квадратного уравнения (4) записывают так:
Отсюда следует, что:
Отсюда следует, что:
- 1) если то уравнение (3) имеет два корня;
- 2) если то уравнение имеет два совпадающих корня;
- 3) если то уравнение не имеет корней.
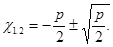
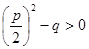
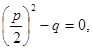
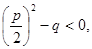
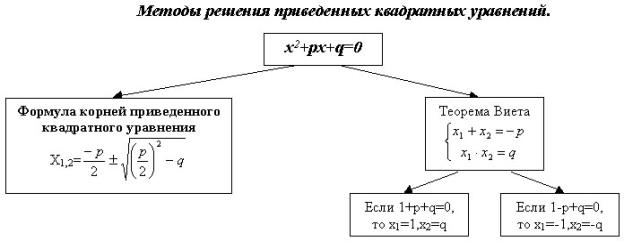
Важным моментом в изучении квадратных уравнений является рассмотрение теоремы Виета, которая утверждает наличие зависимости между корнями и коэффициентами приведенного квадратного уравнения.
Теорема Виета. Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Иначе говоря, если x1 и x2 — корни уравнения х2 +px + q = 0, то.
x1 + x2 = - p,.
x1 x2 = q. (5).
Данные формулы называют формулами Виета в честь французского математика Ф. Виета (1540−1603), который ввел систему алгебраических символов, разработал основы элементарной алгебры. Он был одним из первых, кто числа стал обозначать буквами, что существенно развило теорию уравнений.
Например, приведенное уравнение х2 — 7х +10 = 0 имеет корни 2 и 5. Сумма корней равна 7, а произведение равно 10. Видно, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Справедлива также теорема, обратная теореме Виета.
Теорема, обратная теореме Виета. Если для чисел x1, x2, p, q справедливы формулы (5), то x1 и x2 — корни уравнения х2+px + q = 0 [2,49].
Теорема Виета и теорема, обратная ей, часто применяются при решении различных задач.
Например. Напишем приведенное квадратное уравнение, корнями которого являются числа 1 и -3.
По формулам Виета.
— p = x1 + x2 = - 2,.
q = x1* x2 = -3.
Следовательно, искомое уравнение имеет вид х2 + 2х — 3 = 0.
Сложность освоения теоремы Виета связана с несколькими обстоятельствами. Прежде всего, требуется учитывать различие прямой и обратной теоремы. В прямой теореме Виета даны квадратное уравнение и его корни; в обратной — только два числа, а квадратное уравнение появляется в заключении теоремы. Учащиеся часто совершают ошибку, обосновывая свои рассуждения неверной ссылкой на прямую или обратную теорему Виета.
Например, при нахождении корней квадратного уравнения подбором ссылаться нужно на обратную теорему Виета, а не на прямую, как часто делают учащиеся. Для того чтобы распространить теоремы Виета на случай нулевого дискриминанта, приходится условиться, что в этом случае квадратное уравнение имеет два равных корня. Удобство такого соглашения проявляется при разложении квадратного трехчлена на множители Таким образом, неполные и приведенные квадратные уравнения имеют разные алгоритмы решения, при изучении данной темы необходимо показать, что общая формула корней применима и для этих случаев. Обычно они изучаются перед выводом корней общего квадратного уравнения.
Тема «Квадратные уравнения» очень важна для изучения курса математики средней школы, т. к. является ступенькой в изучении более сложного материала математики средней школы. Умение быстро, рационально и правильно решать квадратные уравнения облегчает прохождение многих тем курса математики. Например, при изучении следующих тем:
- 8-й класс — решение задач на составление квадратных уравнений;
- 9-й класс — разложение квадратного трехчлена на множители; квадратичная функция и ее график; неравенства второй степени с одной переменной;
- 10-й класс — тригонометрические уравнения и неравенства; применение производной к исследованию функции;
- 11-й класс — интеграл; площадь криволинейной трапеции; иррациональные уравнения; показательные уравнения и неравенства; логарифмические уравнения и неравенства.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. На факультативных занятиях с учащимися можно рассмотреть уравнения более сложного уровня, рассмотрев другие способы решения квадратных уравнений:
- 1. Разложение левой части уравнения на множители.
- 2. Метод выделения полного квадрата.
- 3. Решение уравнений способом «переброски».
- 4. Свойства коэффициентов квадратного уравнения.
- 5. Графическое решение квадратного уравнения.
- 6. Решение квадратных уравнений с помощью циркуля и линейки.
- 7. Решение квадратных уравнений с помощью номограммы.
- 8. Геометрический способ решения квадратных уравнений.
Й. Разложение левой части уравнения на множители Примеры:
1.
Решение: Разложим левую часть уравнения на множители:
Следовательно, уравнение можно переписать так:
Произведение равно нулю, когда один из множителей равен нулю.
т.е. или.
Ответ: -12; 2.
2.
Решение:
или
Ответ: -2; -1.
3.
Решение:
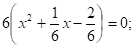
или.
Ответ:

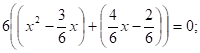
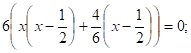
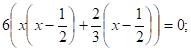
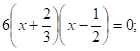
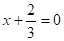

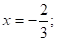
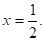
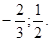
ЙЙ. Метод выделения полного квадрата.
Примеры:
1.
Решение: Выделим в левой части полный квадрат. Для этого запишем выражение х2 +6х в следующем виде: х2 +6х = х2 +2· x·3.
В полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х на 3. Поэтому чтобы получить полный квадрат, нужно прибавить 32, т.к. х2 +2· x·3 +32 =?х+3?2 .
Преобразуем левую часть уравнения х2 +6х -7 =0 прибавляя к ней и вычитая 32. Имеем:
х2 +6х -7 = х2 +2· x·3 + 32 — 32 — 7 =? х +3 ?2 — 9 — 7 =? х + 3 ?2 — 16 .
Таким образом, данное уравнение можно записать так:
? х + 3 ?2 — 16 = 0, т. е.? х + 3 ?2 = 16.
Следовательно, х + 3 = -4, или х + 3 = 4,.
х = -7, х =1.
Ответ: -7; 1.
2.
Решение:
Разделим обе части уравнения на 5, получим.
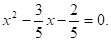
Применим метод выделения полного квадрата.

Следовательно, уравнение можно записать так.
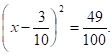
отсюда или.

Ответ:
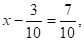
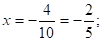
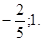
III. Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение.
Умножая обе его части на а, получаем уравнение.
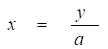
Пусть ах = у, откуда; тогда приходим к уравнению равносильного данному. Его корни у1 и у2 найдем с помощью теоремы Виета.
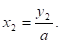
Окончательно получаем и При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
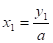
Примеры:
1.
Решение: «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение Согласно теореме Виета.

Ответ: 2,5; 3.
2.
Решение: Используя метод «переброски», получим уравнение По теореме Виета.
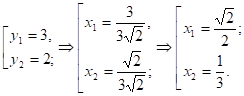
Ответ:

ЙV. Свойства коэффициентов квадратного уравнения.
А. Пусть дано квадратное уравнение.
1. Если, а + в + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то.
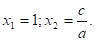
Доказательство: Разделим обе части уравнения на а? 0, получим приведенное квадратное уравнение.
Согласно теореме Виета.
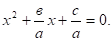
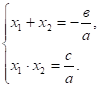
По условию а + в + с = 0, откуда в = - а — с. Значит,.
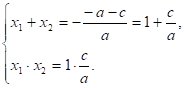
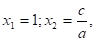
Получаем что и требовалось доказать.
2. Если, а — в + с = 0, или в = а + с, то.
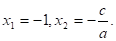
Доказательство: По теореме Виета.
По условию а — в + с = 0, откуда в = а + с. Таким образом,.

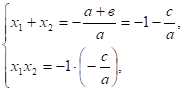
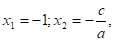
т.е. что и требовалось доказать.
3. Если в уравнении.
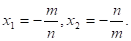
Доказательство: Действительно, приведем это уравнение в виде приведенного.
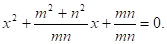
Запишем уравнение в виде.
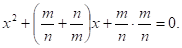
Уравнение, записанное в таком виде, позволяет сразу получить корни.
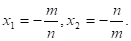
4. Если, а = - с = m· n, в = m2 — n2, то корни имеют разные знаки, а именно:
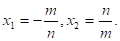
Знаки перед дробями определяются знаком второго коэффициента.
Примеры:
1.
Решение: так как, а + в + с = 0 (2 — 7 + 5 =0), то.
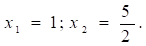
Ответ: 1; 2,5.
2.
Решение: так как 7 — 5 — 2 = 0, то.
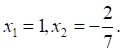
Ответ:
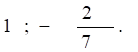
3.
Решение: так как, а — в + с = 0 (5 — 7 + 2 = 0), то.
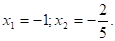
Ответ:
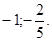
4.
Решение: так как 5 — (-2) + 7 = 0, то.
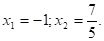
Ответ:
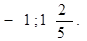
5.
Решение: здесь 6 = 3· 2, 13 = 32 + 22. Корни этого уравнения.
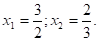
Ответ:
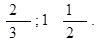
6.
Решение: здесь 6 = 3· 2, но 5 = 32 — 22 и.

Ответ:
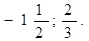
B. Если второй коэффициент в = 2k — четное число, то формулу корней.
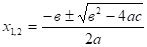
можно записать.
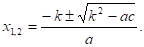
Пример:
Решение: имеем а = 3, в = - 14, с = 16, k = - 7;
D=k2 — ас. D= (-7)2 — 3· 16 = 49 — 48 = 1, D>0, два различных корня;

Ответ:
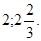
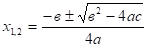
С. Приведенное уравнение совпадает с уравнением общего вида, в котором а = 1, в = p и с = q. Поэтому для приведенного квадратного уравнения формула корней принимает вид или.
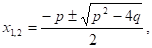
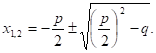
Эту формулу особенно удобно использовать, когда p — четное число.
Пример:
Решение: имеем.
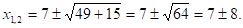
Ответ: -1;15.
V. Графическое решение квадратного уравнения.
Если в уравнении перенести второй и третий члены в правую часть, то получим.
Построим графики зависимостей и.
График первой зависимости — парабола, проходящая через начало координат. График второй зависимости — прямая (рис.1).

Возможны следующие случаи:
- — прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения; - прямая и парабола могут касаться (только одна общая точка), т. е. уравнение имеет одно решение;
- — прямая и парабола не имеют общих точек, т. е. квадратное уравнение не имеет корней.
Примеры:
1. Решить графически.
уравнение.
Решение: см. рис. 2.
Запишем уравнение в виде.
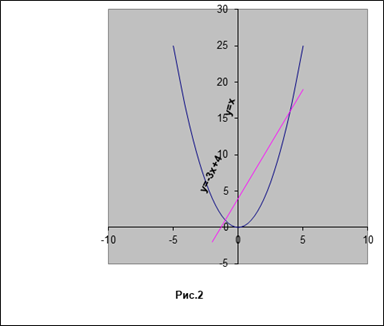
Построим параболу и прямую.
Прямую можно построить по двум точкам М (0;4) и N (3;13). Прямая и парабола пересекаются в двух точках, А и В с абсциссами.
х1 = - 1 и х2 = 4.
Ответ: -1; 4.
2. Решить графически уравнение.
Решение: см. рис. 3. Запишем уравнение в виде.
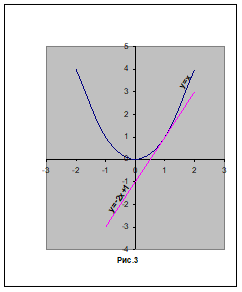
Построим параболу и прямую.
Прямую построим по двум.

точкам М (0;-1) и N.
Прямая и парабола пересекаются.
в точке, А с абсциссой х =1.
Ответ: 1.
3. Решить графически уравнение.
Решение: см. рис. 4.
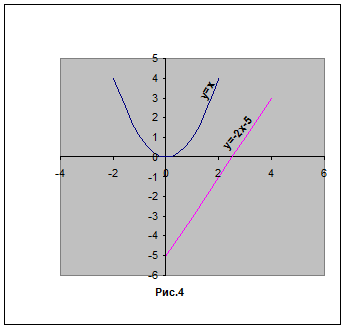
Запишем уравнение в виде.
Построим параболу и прямую. Прямую построим по двум точкам М (0;-5)и N (2,5;0). Прямая и парабола не имеют общих точек пересечения, т. е. данное уравнение не имеет корней.
Ответ: нет решений.
VЙ. Решение квадратных уравнений с помощью циркуля и линейки.
Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.
Предлагаем следующий способ нахождения корней квадратного уравнения.
с помощью циркуля и линейки (рис.5).
Допустим, что искомая окружность пересекает ось абсцисс в точках В (х1;0) и D (х2;0), где х1 и х2 — корни уравнения.
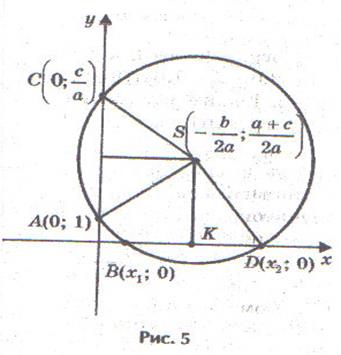
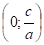
и проходит через точки А (0;1) и С на оси ординат. Тогда по теореме о секущих имеем ОВ· ОD = ОА· ОС, откуда ОС =.

Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд АС и ВD, поэтому.
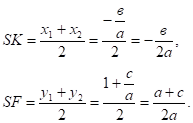
Итак:
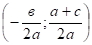
- 1) построим точки S (центр окружности) и А (0;1);
- 2) проведем окружность с радиусом SA;
- 3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
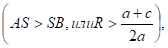
1) Радиус окружности больше ординаты центра окружность пересекает ось Ох в двух точках (рис. 6,а) В (х1;0) и D (х2;0), где х1 и х2 — корни квадратного уравнения.
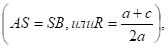
2) Радиус окружности равен ординате центра окружность касается оси Ох (рис. 6,б) в точке В (х1;0), где х1 — корень квадратного уравнения.
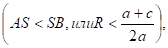
3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис. 6,в), в этом случае уравнение не имеет решения.

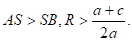
а) Два решения х1 и х2.
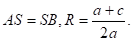
- б) Одно решение х1.
- в) Нет решений.
Примеры:
1.
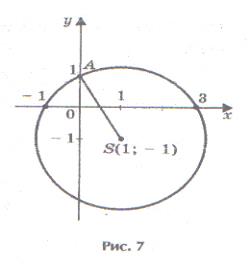
Решение: см. рис. 7.
определим координаты центра окружности по формулам:
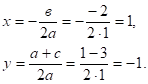
Проведем окружность радиусаSA, где, А (0; 1), S (1; -1).
Ответ: -1; 3.
2.
Решение: см. рис. 8.
определим координаты.
центра окружности по формулам:
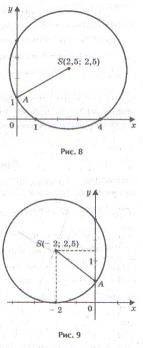
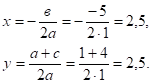
Проведем окружность радиусаSA, где, А (0;1),.
S (2,5; 2,5).
Ответ: 1; 4.
3.
Решение: см. рис. 9.
Определим координаты центра окружности по формулам:

Проведем окружность радиусаSA, где, А (0; 1), S (-2; 2,5).
Ответ: -2.
4.
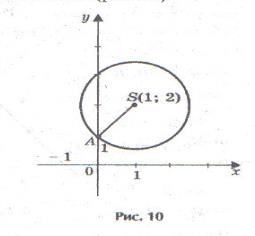
Решение: см. рис. 10.
Определим координаты центра окружности по формулам:
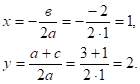
Проведем окружность радиусаSA, где А (0;1), S (1;2).
Ответ: нет решений.
VII. Решение квадратных уравнений с помощью номограммы Это старый и забытый способ решения квадратных уравнений. (см. Четырехзначные математические таблицы. В. М. Брадис. с. 83.).
Таблица XXЙЙ. Номограмма для решения уравнения Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
Криволинейная шкала номограммы построена по формулам (см. рис. 11):
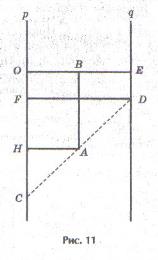
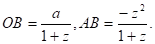
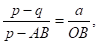
Полагая (все в см.), из подобия треугольников CAH и CDF получим пропорцию откуда после подстановки упрощений вытекает уравнение причем буква z означает метку любой точки криволинейной шкалы.
Примеры:1.

Решение: для уравненияномограмма дает корни z1=8,0 и z2=1,0(рис. 12).
Ответ: 1; 8.
2. .
Решение: разделим обе части уравнения на 2, получим уравнение.
Номограмма дает корни z1=4 и z2= 0,5.
Ответ: 0,5; 4.
3. .
Решение: для уравнения номограмма дает положительный корень z1=1,0, а отрицательный корень находим, вычитая положительный корень из —p, т. е. z2 = -p-1=-5−1=-6,0 (рис. 13).
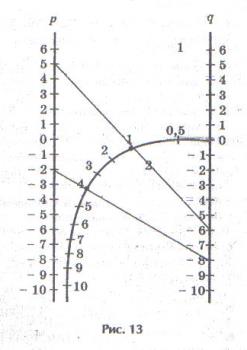
Ответ: -6; 1.
4.
Решение: для решения уравнения номограмма дает положительный корень z1= 4,0,отрицательный корень равен z2 = — p — z1 =2 — 4 = -2,0.
Ответ: -2; 4.
5. .
Решение: для уравнения, оба корня которого отрицательные числа, берем я1 =-1 и находим по номограмме два положительных корня t1 и t2 уравнения это t1 =1 и t2 =3, а затем z1 = - t1 = - 1 и z2 = - t2 = - 3.
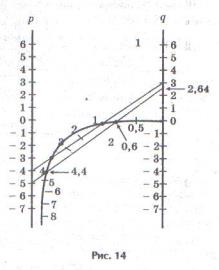
Ответ: -3; -1.
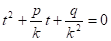
Если коэффициенты p и q выходят за пределы шкалы, то выполняют подстановку z = kt и решают с помощью номограммы уравнение, где k берут с таким расчетом, чтобы имели место неравенства.

6. .
Решение:
для уравнения коэффициенты p и q выходят за пределы шкалы, выполним подстановку z =5t, получим уравнение которое решаем посредством номограммы и получим t1 =0,6 и t2 =4,4, откуда.

Ответ: 3; 22.
X. Геометрический способ решения квадратных уравнений В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведем пример из «Алгебры» ал-Хорезми.
Примеры.
1. .
В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39» (рис. 15).
Решение: Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна, а площадь .
D C.
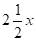
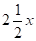


рис. 15. A B

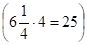
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х2, четырех прямоугольников и четырех пристроенных квадратов, т. е. S = х2 + 10х +25. Заменяя х2 +10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т. е. отрезок AB = 8. Для искомой стороны х первоначального квадрата получим.
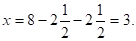
2. А вот, например, как древние греки решали уравнение. Решение представлено на рис. 16, где.
Решение:
Выражения у2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение.
Откуда и получаем, что (рис. 16).
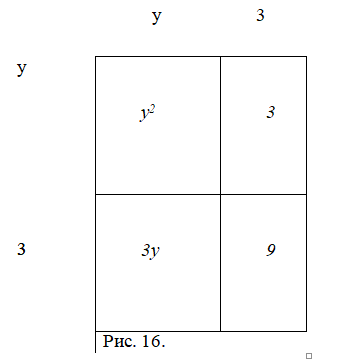
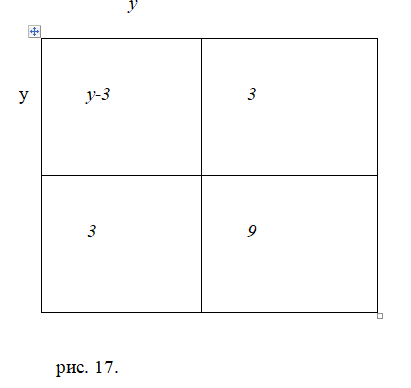
3. .
Решение: преобразуя уравнение, получаем.
На рис. 17 находим «изображения» выражения у2 — 6у, т. е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3.
Заменяя выражение у2 — 6у равным ему числом 16, получаем:
т.е.
Уравнения, приводимые к квадратным.
х — -2= 0.
Решение: замена =а,.
а2 — а — 2 =0,.
т.к. 1+(-2)=-1,.
то а1=-1; а2=2.
.
нет решений. х=4. Ответ: 4.
2. х + -3 =0.
Решение: замена =в,.
в2 +в -2=0,.
т.к. 1+1+(-2)=0,.
то в1=1, в2=-2.
х-1=1, нет решений.
х=2, Ответ: 2.
3. (х2+2х) — (х+1)2 =55.
Решение: т.к. (х+1)2 =х2 +2х +1, то замена х2 +2х =с, с2 — с -56 =0,.
D= (-1)2 — 4· 1·(-56)=225.
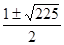
с =,.
с1 =-7, с2 = 8,.
х2 +2х =-7, х2 +2х =8,.
х2 +2х +7 =0, х2 +2х -8=0,.
D=22-4· 1·7=-24, D=22-4· 1·(-8)=36,.
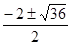
Нет решений. х =,.
х1=-4, х2=2. Ответ: -4; 2.
4. (х2+х+1)2 -3×2 -3х -1=0.
Решение: (х2+х+1)2 -3х2 -3х -3+3 -1=0,.
(х2+х+1)2 -3(х2+х+1) +2 =0,.
замена х2+х+1=t,.
t2 — 3t + 2=0,.
т.к. 1+(-3)+2=0,.
то t1 = 1, t2 = -2,.
х2 +х +1 =1, х2 +х +1 =-2,.
х2 +х =0, х2 +х +3=0,.
х (х +1)=0, D=12-4· 1·3=-11,.
х=0 или х+1=0, нет решений.
х = -1.
Ответ: -1; 0.
5. .
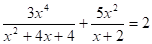
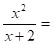

Решение: замена m, тогда m2,.
3m2 +5m -2 =0,.
D=52 -4· 3·(-2)=49,.
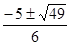
m =,.
m1 =-2, m2 =,.

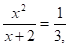
х2 =-2(х+2), 3х2 = х+2,.
х2 +2х +4=0, 3х2 -х -2 =0,.
D=22-4· 1·4=-12, т.к. 3 + (-1) + (-2) =0,.
Нет решений. то х1=1, х2 =-.
Ответ: -; 1.
6. (х2 -5х +7)2 -(х-2)(х-3)=1.
Решение: (х2 -5х +7)2 -(х2 -5х +6) -1=0,.
замена х2 -5х +7 =t,.
t2 — t =0,.
t· (t -1) =0,.
t=0 или t-1=0,.
t=1,.
х2-5х+7=0 или х2-5х+7=1,.
х2-5х+6 =0,.
D=52-4· 1·7=-3, D=52-4· 1·6=1,.

Нет решений. х =,.
х1=2, х2 =3.
Ответ: 2;3.

7. х2 + =5+3х.
Решение: х2 + -5−3х =0,.
замена х2 -3х -2 =n,
n -3 + =0,.
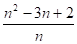
=0,.
n2 -3n +2=0,.
n? 0,.
т.к. 1+ (-3)+2=0,.
то n1 =1, n2 =2,.
х2 -3х -2=1, х2 -3х -2=2,.
х2 -3х -3=0, х2 -3х -4=0,.
D=(-3)2 -4· 1·(-3)=21, D=(-3)2 -4· 1·(-4)=25,.
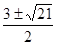
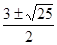
х =; х = ;
х1= -1, х2= 4.
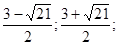
Ответ: -1; 8.
8. (х2 — 6х)2 -2· (х -3)2 =81.
Решение: (х2 — 6х)2 -2· (х2 — 6х +9) =81,.
замена х2 — 6х =z,.
z2 -2z -99 =0,.
D = (-2)2 — 4· 1·(-99)= 400,.

z = ,.
z1 = -9; z2 = 11.
х2 -6х =-9, х2 -6х =11,.
х2 -6х +9 =0, х2 -6х -11 =0,.
(х -3)2 =0, D = (-6)2 -4· 1·(-11) =80,.
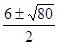
х — 3 =0, х = ,.
х = 3, х = 3±2.
Ответ: 3 -2; 3; 3 +2.
9. =5.

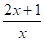
Решение: замена = b,.
b + =5,.

=0,.
b2 -5b +4 =0,.
b? 0,.
b2 -5b +4 =0,.
т.к. 1+(-5)+4=0,.
то b1 =1, b2 =4,.
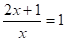

,.
2х+1 =х, 2х+1 =4х,.
х = -1, 2х =1,.
х =0,5.
Ответ: -1; 0,5.

10. 7 -2 =9.

Решение: замена ,.
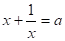
.
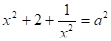

.
.
.
т.к. (-2) + 7 +(-5) =0,.
то, ,.
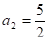
,.

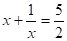
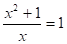
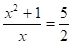
,.
,.
,.
D= (-1)2 -4· 1·1=-3, D=(-5)2 -4· 2·2=9,.
Нет решений. ,.
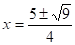
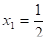
.
Ответ: 0,5; 2.
11. .
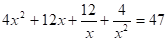
Решение: ,.
замена ,.
.
.
.
.
D=122 -4· 4·(-55)=1024,.
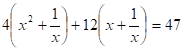
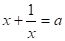

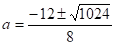
.
; ,.
; ,.

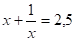

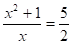
; ,.
,.
,.
D=112 — 4· 2·2=105, D=(-5)2 — 4· 2·2=9,.
х =; х =;

х1 =; х2 =2.
Ответ:

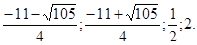
12.

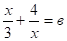

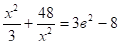
Решение: замена, тогда, .
т.к. 3+5+(-8)=0, то в1 =-1, в2 =.
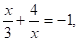
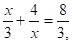
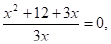
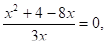
D =32 -4· 1·12=-39, D =(-8)2 -4· 1·4=12,.
Нет решений. ;
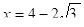
Ответ:
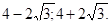
13. х4 — 2×3 — х2 — 2х + 1 =0.
Решение: пусть х2?0, тогда обе части уравнения разделим на х2.
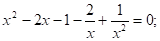
замена.
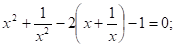

т.к. 1+2+(-3)=0,то.
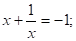
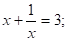

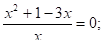
D = 12 -4· 1·1=-3, D =(-3)2 — 4· 1·1=5,.
Нет решений.

Ответ:
14.
Решение:
замена.
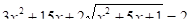
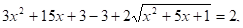
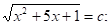
т.к. 3+2+(-5)=0,то.

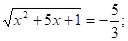
нет решений.
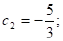
D =52 -4· 1·1=21,.
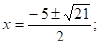
Ответ:
15.
Решение:
- 0
- 0
- 0
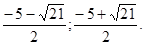


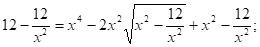
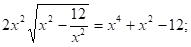

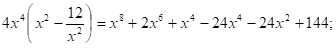
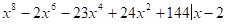
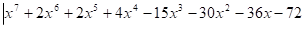


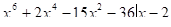
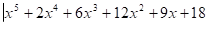

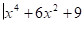
Нет решений.
Проверка:
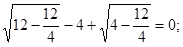
х=2; 0=0;
х=-2; 0=0.
Ответ: -2; 2.
Уравнения, сводящиеся к квадратным.
1. 4×4 — 5×2 + 1 = 0.
Решение: пусть х2 = t, тогда 4t2 — 5t + 1 = 0,
D=25 — 24 = 1>0,.

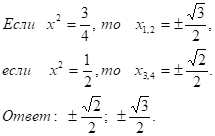
2. (6×2 — 7х)2 — 2(6×2 — 7х) — 3 = 0.
Решение: пусть 6х2 — 7х = у, тогда данное уравнение примет вид у2 — 2у — 3 = 0, откуда у1 = 3, у2 = - 1.
Учитывая подстановку, получим 2 квадратных уравнения:

3. (х + 1)(х + 2)(х + 3)(х + 4) = 1680.
Решение: запишем данное уравнение в виде.
- (х + 1)(х + 4)(х + 2)(х +3) = 1680 или
- (х2 + 5х + 4)(х2 + 5х + 6)=1680.
Пусть х2 + 5х + 5 = у, тогда уравнение примет вид.
(у — 1)(у + 1)=1680 или у2 — 1 = 1680, у2 = 1681,
откуда у1,2 = ± 41.
Имеем два квадратных уравнения:
- а) х2 + 5х + 5 = 41, х2 + 5х — 36 = 0, откуда х1 = - 9, х2 = 4.
- б) х2 + 5х + 5 = - 41, х2 + 5х + 46 = 0, D=25 — 4· 46=-159<0 — нет корней.
Итак, исходное уравнение имеет два корня .
Ответ: — 9; 4.
4. (х + 5)2 — 13(х + 5)2×2 + 36×4 = 0.
Решение: выделим в левой части полный квадрат, для чего прибавим к обеим частям по 25(х + 5)2х2.
Данное уравнение примет вид.
- (х + 5)4 + 12(х + 5)2х2 + 36х4 = 25(х + 5)2х2;
- ((х + 5)2 + 6х2)2 = (5(х + 5) х)2, откуда имеем:
- а) (х + 5)2 + 6х2 =5(х + 5) х,
- 7х2 + 10х + 25 =5х2 + 25х, 2х2 — 15х + 25 = 0,
D=225 — 200 = 25 = 52>0,
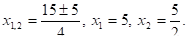
б) 7х2 + 10х + 25 = -5х2 — 25х, 12х2 + 35х + 25 = 0,.
D=1225 — 1200 = 25 = 52>0,
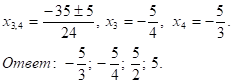
5. 2(х2 — х + 1)2 = х2(8×2 — 5х + 5).
Решение: запишем данное уравнение в виде.
2(х2 — х + 1)2 = 5х2(х2 — х + 1) + 3х4. (1)
Заметим, что уравнение (1) является однородным относительно х2 — х + 1 и х2 и потому, разделив обе части полученного уравнения на.
х2(х2 — х + 1)? 0, получим.
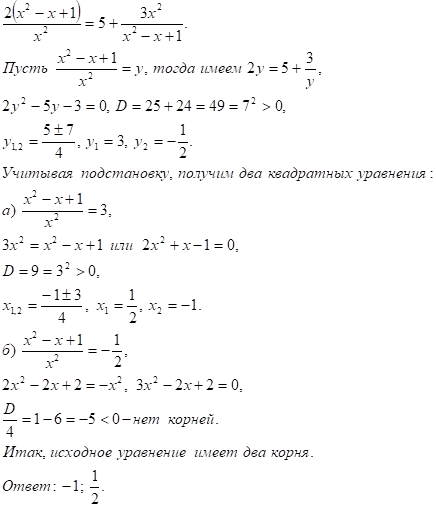
6. х4 — 10×3 + 35×2 — 50х + 24 = 0.
Решение: уравнение можно решить, перебирая все делители свободного члена. Однако это уравнение допускает более короткое и изящное решение:
(х2 — 5х)2 + 10(х2 — 5х) + 24 = 0, откуда по обратной теореме Виета получим х2 — 5х = - 4 или х2 — 5х = - 6.
Если х2 — 5х = - 4, то х2 — 5х + 4 = 0, х1 = 1, х2 = 4,
если х2 — 5х = - 6, то х2 — 5х + 6 = 0, х1 = 2, х2 = 3.
Ответ: 1; 2; 3; 4 .
Распадающиеся уравнения.
1. (х2 — 5х + 6)(х2 + х — 2) = 0. (1).
Решение: если число х0 есть корень уравнения (1), то подставляя х0 вместо х в уравнение (1), получим верное числовое равенство.
(х02 — 5х0 + 6)(х02 + х — 2)= 0. (2).
Но произведение двух чисел равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Поэтому из (2) следует, что х0 есть корень хотя бы одного из уравнений.
х2 — 5х + 6 = 0 (3) или х2 + х — 2 = 0 (4).
другой стороны, любой корень любого из уравнений (3) или (4) есть корень уравнения (1).
Таким образом, множество всех корней уравнения (1) есть объединение множества всех корней уравнения (3) и множества всех корней уравнения (4).
Уравнение (3) имеет корни х1 = 2 и х2 =3, а уравнение (4) — корни х3 = -2 и х4 =1.
Следовательно, уравнение (1) имеет корни -2; 1; 2; 3 и других корней не имеет.
Ответ: -2; 1; 2; 3.
Говорят, что уравнение распадается на два уравнения, если множество всех его корней есть объединение множества всех корней этих двух уравнений.
2. х3 — 1 = 0.
Решение: это уравнение распадается на два уравнения:
х — 1 = 0 и х2 + х + 1 = 0,
потому что х3 — 1 = (х — 1)(х2 + х + 1).
Первое уравнение имеет корень х = 1, второе уравнение не имеет корней.
Следовательно, данное уравнение имеет единственный корень х = 1.
Ответ: 1.
3. х6 — 1 = 0.
Решение: уравнение распадается на три уравнения:
х — 1 = 0, х + 1 = 0 и х4 + х2 + 1 = 0,
потому что х6 — 1 = (х2 — 1)(х4 + х2 + 1)=(х -1)(х +1)(х4 + х2 +1).
Первые два уравнения имеют корни х1 = 1 и х2 = - 1, третье же уравнение не имеет корней, т.к. это биквадратное уравнение при замене х2 = у, получаем квадратное уравнение у2 + у + 1 = 0, которое не имеет корней т.к. D= 12 — 4· 1·1= - 3 < 0.
Следовательно, данное уравнение имеет два корня.
Ответ: -1; 1 .
4. х3 — 2×2 — 3х = 0.
Решение: так как х3 — 2х2 — 3х =х (х2 — 2х — 3), то данное уравнение распадается на два уравнения.
х = 0 и х2 — 2х — 3 = 0.
Второе имеет два корня х1,2 = 1 ± = 1 ± 2,
тогда данное уравнение имеет три корня.
Ответ: — 1; 0; 3.
В целом можно сказать, что освоение темы «Квадратные уравнения» поднимает учащихся на качественно новую ступень овладения содержанием школьной математики.