Разработка модели системы массового обслуживания для оптимизации количества офисов ООО «Промтрансбанк»

В настоящее время на практике возникла необходимость в решении различных вероятностных задач, связанных с работой так называемых систем массового обслуживания (СМО). Системами массового обслуживания называются системы, в которых, с одной стороны, возникают массовые запросы (требования) на выполнение каких-либо видов услуг, а с другой стороны, происходит удовлетворение этих запросов.

На рисунке 5 представлен граф состояний многоканальной СМО с ожиданиями.

… …

… …

Pис. 5. Размеченный граф состояний многоканальной СМО с ожиданиями Состояния СМО имеют следующую интерпретацию:

S0 — все каналы свободны;

S1 — занят один канал, остальные свободны;

Sn — заняты все n каналов, очереди нет;

Sk — заняты все n каналов, r заявок в очереди, k=n+r;

Определим интенсивности потоков событий, переводящих систему по стрелкам справа налево.

Пусть система находиться в состоянии S1 (занят один канал). Тогда, как только закончиться обслуживание заявки, занимающей этот канал, система перейдет в S0; значит, поток событий, переводящий систему по стрелке S1 S0, Имеет интенсивность µ. Очевидно, если обслуживанием занято два канала, а не один, поток обслуживаний, переводящий систему по стрелке S2 S1, будет вдвое интенсивнее (2µ); если занято k каналов — в k раз интенсивнее (kµ). Проставим соответствующие интенсивности у стрелок, ведущих справа налево.

Из рисунка 5 видно, что процесс, протекающий в СМО, представляет собой частный случай процесса гибели и размножения.

Пользуясь общими правилами, можно составить уравнения Колмогорова для вероятностей состояний.

Уравнения (15) называются уравнениями Эрланга.

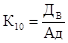
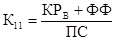
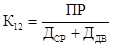
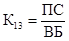
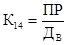
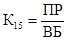
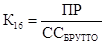
= - лp0 + µp1.

= - (л+µ)p1 + лp0+2µp1.

…

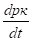
= - (л+kµ)pk + лpr-1+(k+1)µpk+1.

…

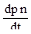
= - n µpn + лpn-1, (15).

Естественными начальными условиями для их решения являются:

p0(0)=1; p1(0)=p2(0)=…=pn (0)=0 (в начальный момент система свободна).

Интегрирование системы уравнений (1) в аналитическом виде довольно сложно; на практике такие системы дифференциальных уравнений обычно решаются численно, на АВМ или ЭЦВМ. Такое решение дает нам все вероятности состояний.

p0(t), p1(t),…, pn (t) как функции времени.

Естественно, нас больше всего будут интересовать предельные вероятности состояний p0, p1 ,…, pk ,…, pn, характеризующие установившийся режим работы СМО (при t ?). Для нахождения предельных вероятностей воспользуемся уже готовым решением задачи, полученным для схемы гибели и размножения. Согласно этому решению,.

pk = (k = 1, 2, …, n).

po =.

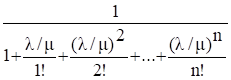
В этих формулах интенсивность потока заявок л и интенсивность потока обслуживаний (для одного канала) µ не фигурируют по отдельности, а входят только своим отношением л/µ. Обозначим это отношение: л /µ=p и будем называть величину p «приведенной интенсивностью» потока заявок. Физический смысл ее таков: величина p представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.

С учетом этого обозначения, формулы (16) примут вид:

pk = (k = 1, 2, …, n).

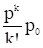
po =.

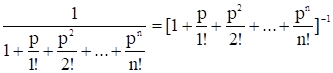
Формулы (17) называются формулами Эрланга. Они выражают предельные вероятности всех состояний системы в зависимости от параметров л, µ и n (л — интенсивность потока заявок, µ - интенсивность обслуживания, n — число каналов СМО). Зная все вероятности состояний p0, p1 ,…, pk ,…, pn, пропускную способность q, абсолютную пропускную способность, А и вероятность отказа Pотк. Действительно, заявка получает отказ, если приходит в момент, когда все n каналов заняты. Вероятность этого равна:

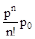
Ротк = pn = ,(18).

Вероятность того, что заявка будет принята к обслуживанию (она же относительная пропускная способность q) дополняет Pотк до единицы:

q = 1- pn, (19).

Абсолютная пропускная способность:

A = л q = л (1- pn),(20).

Одной из важных характеристик СМО с отказами является среднее число занятых каналов (в данном случае оно совпадает со средним числом заявок, находящихся в системе). Обозначим это среднее число k-. Величину kможно вычислить непосредственно через вероятности p0, p1,…, pn по формуле:

= 0*p0 + 1 * p1 + … + n * pn,(21).

как математическое ожидание дискретной случайной величины, принимающей значения 0,1,…, n с вероятностями p0, p1,…, pn. однако значительно проще выразить среднее число занятых каналов через абсолютную пропускную способность А, которую мы уже знаем. Действительно, А есть не что иное, как среднее число заявок, обслуживаемых в единицу времени; один занятый канал обслуживает в среднем за единицу времени µ заявок; среднее число занятых каналов получится делением, А на µ:

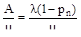
=, (22).

или, переходя к обозначению л / µ = p,.

= p (1-pn), (23).

Рассмотрим подробнее математическую модель работы банка как системы массового обслуживания. Для решения задачи было принято допущение, что очередь клиентов в банке ограничена, и, следовательно, данная модель является n-канальной СМО с ожиданием, где n — количество касс обслуживания. Поток заявок (клиентов банка) в систему поступают с интенсивностью 35 чел. (л), а 20 чел. — интенсивность обслуживания (µ) каждого канала (кассир-операционист банка). Каналов в банке 5 единиц (касс). Характеристиками эффективности обслуживания клиентов банка будут являться — среднее число заявок в очереди, среднее время ожидания в очереди, среднее время обслуживания заявки, а также процент загруженности касс.

На рисунке 6 представлены исходные и расчетные данные по ООО «Промтрансбанк».

Рис. 6. Многоканальная модель с ограниченной очередью для ООО «Промтрансбанк»

На рисунке 6 представлен лист с готовыми суммами, на рисунке 7 представлен такой же лист, но с содержанием всех необходимых формул, с помощью которых были получены данные.

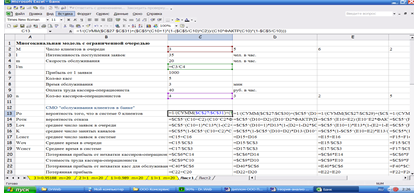
Рис. 7. Порядок расчетов при многоканальной модели с ограниченной очередью

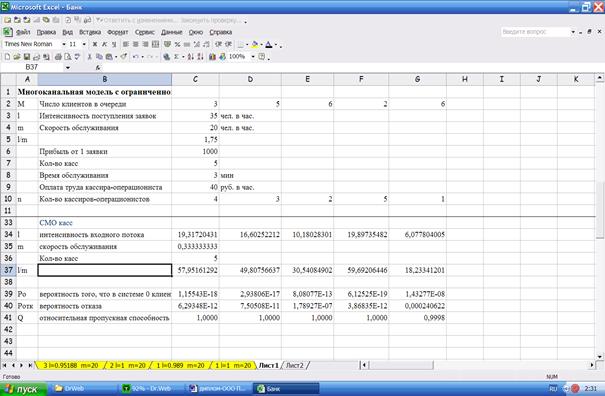
Рис. 8. СМО касс для ООО «Промтрансбанк»

На рисунке 9 приведены результаты расчетов по формулам теории СМО.

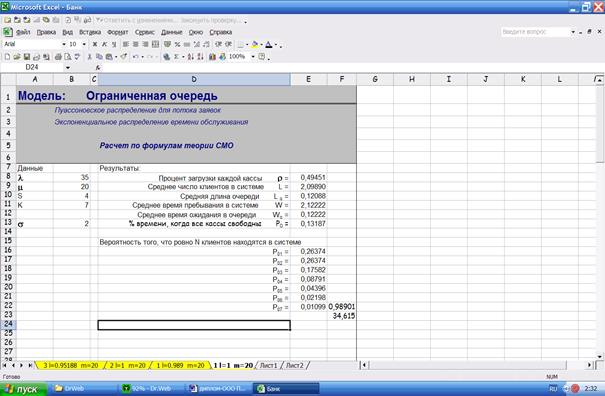
Рис. 9. Результаты расчетов по формулам теории СМО

В результате проведенного исследования сформулированы следующие выводы:

Р0 =0,13 187. Это значит? что практически всегда присутствует на в банке хотя бы один клиент.

p=0,49 451. Это вероятность того, что все кассы заняты обслуживанием клиентом. Это значит, что практически всегда присутствует в банке хотя бы один клиент который обслуживается.

Вероятность времени ожидания в очереди W0 равна 0,12 222. Это значит, что клиенты стоят в очереди.

Среднее время, в течение которого клиент ждет начала обслуживания равно 2,12 222. Это значит, что клиенты стоят в очереди примерно 2 минуты 12 сек.

Средняя длина очереди равна 0,12 088. Это значит, что в среднем очередь состоит из 1 клиента.

Среднее число обслуживаемых клиентов равно 2,9 890. Это означает, что в среднем в банке одновременно обслуживается почти три клиента.

Практическая значимость данной работы очевидна: модель позволяет не только наглядно продемонстрировать процесс обслуживания банком клиентов, но и может путем экспериментов выявить наиболее оптимальное распределение ресурсов для повышения эффективности его работы. Также можно предположить применение данной модели на реальном объекте.