Разработка методики проведения курса по выбору «дедуктивные рассуждения в математике» для 9 класса

Разработка содержания курса по выбору При разработке курса по выбору особое внимание было уделено содержанию курса.

Изучив принципы отбора содержания учебного материала для предметных курсов по выбору, представленные Смирновой И. М. [51], покажем, как каждый из этих принципов учитывался при разработке содержания курса.

• • Критерий целостности содержания. Курс направлен на изучение. Целостность содержания данного курса заключается во внутренней взаимосвязи всего курса вокруг дедуктивных рассуждений и связанных с ними логических понятий, законов и правил логики.
• • Критерий преемственности содержания основного курса и курса по выбору. Одной из основных целей школьного математического образования является приобретение навыков логического мышления, умения правильно рассуждать. Разработанный курс по выбору призван развить умение учащихся правильно рассуждать с помощью применения средств формальной логики.
• • Критерий научной и практической значимости. Данный критерий реализуется благодаря решению логических задач из ЕГЭ по математике, при обучении дедуктивным рассуждениям с использованием средств формальной логики. Помимо известных учащимся сведений в курсе содержится материал, выходящий за рамки школьной программы.
• • Критерий соответствия содержания воспитательным и развивающим целям обучения. При изучении математики необходимо использовать дедуктивные рассуждения, так как именно умение правильно рассуждать воспитывают строгость, четкость и лаконичность мышления.
• • Критерий соответствия содержания возрастным особенностям школьников. Наш курс содержит посильный материал для школьников, соответствующий их уровню развития. Как показала опытно-экспериментальная проверка, предложенный для изучения материал доступен учащимся.
• • Критерий соответствия содержания индивидуальным особенностям школьников. Учитывая индивидуальные особенности и интересы школьников, в нашем курсе используются различные виды и формы учебной деятельности.
• • Критерий соответствия содержания учебно-методическому обеспечению. Разработаны: программа (пояснительная записка, содержание основных разделов курса), тематическое планирование, несколько конспектов занятий, материалы для проверочных работ; подобран набор задач по темам, а также список рекомендуемой литературы для школьников и учителей.
• • Критерий соответствия содержания имеющемуся времени. Курс состоит из 16 занятий. Объем учебного материала каждого занятия соответствует времени, отведенному на его изучение.

Программа курса по выбору Пояснительная записка Курс по выбору «Дедуктивные рассуждения в математике» предназначен для обучающихся в 9 классе, планирующих продолжить обучение в 10 классе, где одним из профилирующих предметов является математика.

Формирование логической культуры учащихся является одним из важнейших условий современного образования. Умение логически грамотно рассуждать, отчётливо формулировать свои мысли и делать верные выводы требуется на всех учебных предметах, а также и в жизни. Учащиеся в некоторой степени умеют рассуждать, но недостаточно, нередко допускают логические ошибки. Владение элементарным комплексом логических понятий, операций и правил дедукции позволит развить у школьников умение логически правильно рассуждать.

В школьном курсе математики обучению дедуктивным (логически правильным) рассуждениям не уделяется досточного внимания. В рамках курса по выбору учащиеся смогут углубить и обобщить ранее приобретённые знания, узнают некоторые важные законы и правила формальной логики, узнают, что такое логическое следование, научатся выявлять логическую форму предложений и правильно записывать их символически, распознавать правильные и неправильные рассуждения, а также научатся применять полученные знания в жизни и к решению задач: на проведение анализа рассуждений, на выведение следствий и т. п.

Разработанный курс по выбору относится к предметно-ориентированным курсам. Данный курс будет интересен всем учащимся 9 класса, так как он направлен на развитие познавательных интересов, логического мышления, умения правильно рассуждать.

Цели курса:

учебные: изучение элементов формальной логики, развитие умения распознавать правильные и неправильные рассуждения, применение полученных знаний при решении задач на рассуждения.

развивающие: развитие логического мышления обучающихся; развитие познавательного интереса у учащихся к математике, развитие у учащихся навыков применения дедукции.

воспитательные: воспитание нравственных качеств личности: целеустремлённости, настойчивости, трудолюбия, дисциплинированности, самостоятельности; формирование коммуникативной культуры личности, организация опыта сотрудничества, взаимопомощи, взаимной поддержки.

Задачи курса:

• • научить переходить от предложения в безусловной форме к предложению с тем же смыслом в условной форме;
• • научить выявлять логическую форму предложений и правильно записывать их символически;
• • научить для данного предложения распознавать предложения: обратное данному, противоположное данному и обратное противоположному;
• • сформировать представление об отношениях следования и равносильности;
• • сформировать представление о правильных и неправильных рассуждениях;
• • подготовить к решению логических задач из ЕГЭ по математике. В результате изучения курса учащиеся должны знать:
• • логические термины и понятия: предложения без переменных (высказывания) и с переменными; логические операции над предложениями; обратное, противоположное и обратное противоположному предложения для данного предложения; логически равносильные предложения; логическое следствие;
• • законы и правила логики;
• • взаимосвязь между равносильностью и следованием;
• • отличие дедуктивных рассуждений от индуктивных;
• • значение дедуктивных рассуждений в математике.

В результате изучения курса учащиеся должны уметь:

• • переходить от предложения в безусловной форме к предложению с тем же смыслом в условной форме;
• • выявлять логическую форму предложений;
• • записывать символически предложения и рассуждения;
• • для данного условного предложения распознавать предложения: обратное данному, противоположное данному и обратное противоположному;
• • распознавать/выводить следствия данного предложения;
• • распознавать правильные и неправильные рассуждения;
• • проводить правильные рассуждения;
• • решать логические задачи из ЕГЭ по математике.

Изучение курса осуществляется посредством применения различных форм проведения занятий: лекции, беседы, семинары. Формы организации учебной деятельности учащихся на занятиях: фронтальная, индивидуальная, групповая, подготовка выступлений и докладов. На занятиях, посвящённых изучению теоретического материала, можно использовать презентации Power Point, с целью реализации принципа наглядности, лучшего усвоения учащимися изучаемого материала, а также экономии времени на уроке.

Курс рассчитан на 16 уч.ч. по одному занятию (1 уч.ч.) в неделю.

Рекомендуемая литература для учащихся.

• 1. Высоцкий И.Р., Ященко И. В. ЕГЭ. Математика для нелюбителей. Подготовка к ЕГЭ. Базовый уровень. — М.: Издательство «Экзамен», 2017. 303 с.
• 2. Никольская И. Л., Семенов Е. Е. Учимся рассуждать и доказывать: Кн. для учащихся 6−10 кл. средн. шк. — М.: Просвещение, 1989. — 192 с.
• 3. Столяр А. А. Зачем и как мы доказываем в математике: Беседы со старшеклассником. — Мн.: Нар. асвета, 1987. — 143 с.

Рекомендуемая литература для учителей.

• 1. Никольская И. Л. Знакомство с математической логикой. — М.: Московский психолого-социальный институт: Флинта, 1998. — 128 с.
• 2. Пойа Д. Математика и правдоподобные рассуждения / Д. Пойа. — М.: Наука, 1975. — 463 с.
• 3. Столяр А. А. Логические проблемы преподавания математики. Минск: «Высшая школа», 1965. — 254 с.
• 4. Тимофеева И. Л. Вводный курс математики: учеб. пособие для студентов учреждений высш. пед. проф. образования / И. Л. Тимофеева, И. Е. Сергеева, Е. В. Лукьянова; под ред. В. Л. Матросова. — М.: Издательский центр «Академия», 2011. — 240 с.
• 5. Факультативный курс по математике: Учеб. пособие для 7−9 кл. сред. шк. / Сост. Никольская И. Л. — М.: Просвещение, 1991. — 383с.
• 6. Ященко И. В., Шестаков, С. А. Подготовка к ЕГЭ по математике в 2017 году. Базовый уровень. Методические указания. — М.: МЦНМО, 2017. — 270 с. Содержание курса по выбору

Основным объектом изучения курса по выбору «Дедуктивные рассуждения в математике» являются дедуктивные рассуждения, т. е. рассуждения, опирающиеся на законы и правила формальной логики. Основной раздел курса — второй, посвящённый распознаванию правильных и неправильных рассуждений. Не менее важным является и первый раздел, в котором представлен необходимый теоретический материал, направленный на выявление формы предложений, их символическую запись, изучение логических законов и правил. После овладения этим материалом (теоретической базой) и соответствующими умениями, учащийся способен распознавать правильные и неправильные рассуждения с использованием средств логики.

Содержание основных разделов программы курса по выбору.

I. Логические операции над предложениями. Равносильность и следование.

• 1. Логические операции над предложениями. Предложения без переменных (высказывания). Логические операции над высказываниями: конъюнкция, дизъюнкция, импликация, отрицание, эквиваленция. Предложения с переменными. Логические операции над предложениями с переменными. Кванторные слова и кванторы.
• 2. Логическое строение математических предложений. Символическая запись предложений. Условная и безусловная формы предложений.
• 3. Обратное, противоположное и обратное противоположному предложения для данного. Предложение, обратное данному. Предложение, противоположное данному. Предложение, обратное противоположному для данного.
• 4. Равносильность и следование. Равносильные предложения. Логически равносильные предложения. Законы логической равносильности. Следствие данного предложения (данных предложений). Логическое следование. Свойства логического следования. Логическая взаимосвязь между данным предложением и предложением, обратным противоположному. Правила рассуждения.

II. Дедуктивные рассуждения.

• 1. Индуктивные и дедуктивные рассуждения. Роль индуктивных и дедуктивных рассуждений в разных областях знаний. Примеры. Значение дедуктивных рассуждений в математике.
• 2. Задачи на распознавание следствий и на выбор предложений, верных при данных условиях. Пропедевтические задачи. Задачи на распознавание следствий. Задачи на выбор верных предложений.
• 3. Задачи на распознавание правильных рассуждений. Логическое строение и схема рассуждения. Правильная схема. Правильное рассуждение. Задачи на распознавание правильных рассуждений. Задачи на построение правильных рассуждений.

Тематическое планирование курса по выбору Таблица 1 — Тематическое планирование курса по выбору.

Учебно-методические материалы для курса по выбору Представим материалы для занятий по некоторым темам. Для разработки материалов мы использовали источники [20], [58], [61]. Изложим теоретические материалы, вопросы, упражнения и задачи.

1. Материал для занятия «Логические операции над предложениями» Высказывания. При изучении математики мы имеем дело с математическими предложениями. Отметим, что они являются повествовательными. Математические предложения могут содержать переменные, которым можно придавать разные значения, а могут и не содержать. Например, предложение «х — четно» содержит переменную, а предложение «4 — четно» нет.

Под высказыванием будем понимать повествовательное предложение, о котором имеет смысл говорить, что оно истинно или, что оно ложно. Высказывание не содержит переменных, которым можно придавать значения.

Вопросы и ответы.

а) Вопрос: Предложение «5<5» является высказыванием? (Ответ: Да.) Вопрос: Оно истинно или ложно? (Ответ: Ложно.).

б) Вопрос: Предложение «5?5» является высказыванием? (Ответ: Да.) Вопрос: Оно истинно или ложно? (Ответ: Истинно.).

Вопрос: Почему? (Ответ: Это высказывание является дизъюнкцией двух высказываний «5>5 или 5=5», которое истинно тогда и только тогда, когда истинно хотя бы одно из двух высказываний («5=5»).).

Импликация высказываний. Импликацией высказываний А и B называют выказывание «Если А, то В». Обозначают это высказывание так: А>В. Высказывание «Если А, то В» считают ложным тогда и только тогда, когда высказывание А истинно, а высказывание В ложно.

Высказывание А называют посылкой, а высказывание В —

заключение

м импликации А>В.

Таблица 2 — Таблица истинности для импликации.

Если посылка импликации ложна, то импликация истинна независимо от значения заключения. Это свойство импликации часто выражают фразой «Из лжи следует всё, что угодно».

Вопрос: Когда импликация ложна? (Ответ: В единственном случае: когда посылка истинна, а заключение ложно.).

Методический комментарий. При изучении темы «Логические операции над предложениями» после введения определения логической операции импликации можно обсудить с учащимися следующий вопрос: Когда импликация истинна? Учащиеся ответят на этот вопрос в соответствии с таблицей истинности для данной операции (таблица 2), т. е. в трёх случаях. Учителю необходимо показать учащимся на данном примере, что из этих трёх случаев можно объединить 3 и 4 строки, когда посылка ложна, и 1 и 3 строки, когда заключение истинно, т. е. импликация истинна, когда посылка ложна или заключение истинно.

Вопросы и ответы.

а) Вопрос: Предложение «Если 2 — простое число, то 2 — чётное число» является высказыванием? (Ответ: Да.).

Вопрос: Оно истинно или ложно? (Ответ: Истинно.).

Вопрос: Почему? (Ответ: Это высказывание — импликация, она истинна, поскольку её посылка и заключение — истинные высказывания.).

б) Вопрос: Предложение «Если 7 — составное число, то 7 — чётное число» является высказыванием? (Ответ: Да) Вопрос: Оно истинно или ложно? (Ответ: Истинно.).

Вопрос: Почему? (Ответ: Это высказывание — импликация, она истинна, поскольку её посылка — ложное высказывание.).

в) Вопрос: Предложение «5 · х = 20» является высказыванием?

Методический комментарий. Если учащийся даст ответ «да», то следует задать вопрос: «Истинное оно или ложное?». Они ответить точно не смогут.

Вопрос: Если переменной x придать значение 4, какое получим высказывание? (Ответ: Истинное.).

Вопрос: Если переменной x придать другое значение, например, 5, то какое получим высказывание? (Ответ: Ложное.).

Значит, предложение «5 · х = 20» не является высказыванием, потому что не имеет смысла говорить, что оно истинно или, что оно ложно. Это предложение с действительной переменной. Переменной x можно придавать значения из множества ??, т. е. заменять её действительными числами. В результате будут получаться разные высказывания.

Предложения с переменными. В математике очень часто встречаются предложения с одной или несколькими переменными, которые превращаются в высказывания, если переменным придавать какие-либо значения из заданного множества.

Пример. Предложение «5 · х = 20» является предложением с переменной.

Будем говорить «верно предложение б (x)», если для любого а из множества М истинно высказывание б (а).

Вопросы и ответы.

Пусть x — действительная переменная.

а) Вопрос: Предложение «x2? 0» верно? (Ответ: Да.).

Вопрос: Почему? (Ответ: Потому что оно истинно для любой переменной x.).

б) Вопрос: Предложение «x > 0» верно? (Ответ: Нет.).

Вопрос: Почему? (Ответ: Потому что оно не будет истинным для любой переменной x.).

3. Материал для занятия «Обратное, противоположное и обратное противоположному предложения для данного».

Предложение вида «Если…, то…» называют предложением в условной форме. С каждым предложением в условной форме «Если А(х), то В(х)» связаны три предложения: обратное, противоположно и обратное противоположному.

Обратное предложение. Рассмотрим предложение «Если А(х), то В(х)». Предложение «Если В(х), то А(х)» называется обратным предложению.

«Если А(х), то В(х)».

Чтобы получить предложение, обратное данному, надо просто поменять местами посылку и заключение. Отсюда и употребление слова «обратное»: в обратном предложении посылка и заключение идут в обратном порядке.

Символически запишем данное предложение так: А(х) > В(х), а предложение, обратное данному, так: В(х) > А(х).

Таблица 3 — Обратное предложение.

Упражнение. Постройте предложение, обратное предложению «Если В(х), то А(х)»? (Предложение «Если А(х), то В(х)»).

Предложения «Если А(х), то В(х)» и «Если В(х), то А(х)» называют взамно обратными.

Упражнение. Дано предложение (известно, что оно верно):

Если Соня выходит из дома, то она выключает телевизор.

Постройте предложение, обратное данному.

Решение. Обратное данному: Если Соня выключает телевизор, то она выходит из дома.

Вопрос: Известно, что данное предложение верно. Верно ли обратное?

Чтобы ответить на этот вопрос, выполним следующее упражнение.

Упражнение. Известно следующее:

Если Соня выходит из дома, то она выключает телевизор.

Приведите ещё примеры условий, когда Соня может выключать телевизор.

Решение. Соня может выключать телевизор, если она делает уроки.

Соня может выключать телевизор, если она ложится спать. Соня может выключать телевизор, если она читает книжку. Соня может выключать телевизор, если она слушает музыку.

Таким образом, пример показывает, что если Соня выключает телевизор, то она при этом может выходить из дома, а может и не выходить.

Вывод. Предложение, обратное верному предложению, может не быть верным. Противоположное предложение. Предложение «Если не-А(х), то не-В(х)» называется противоположным предложению «Если А(х), то В(х)».

Запишем символически предложение, противоположное данному, так:

не-А(х) > не-В(х).

Таблица 4 — Противоположное предложение.

Упражнение. Дано предложение (известно, что оно верно):

Если Соня выходит из дома, то она обязательно выключает телевизор.

Постройте предложение, противоположное данному.

Решение. Противоположное данному: Если Соня не выходит из дома, то она не выключает телевизор.

Вопрос: Если Соня не выходит из дома, обязательно ли она не выключает телевизор? Верно ли противоположное? (Ответ: Мы не можем утверждать, что противоположное является верным, потому что Соня, когда не выходит из дома, может как выключать телевизор, так и не выключать его.).

Вывод. Предложение, противоположное верному предложению, может и не быть верным.

Предложение, обратное противоположному: «Если не-В(х), то не-А(х)»

Упражнение. Для предложения «Если А(х), то В(х)» постройте предложение, обратное противоположному.

Решение. Данное предложение: «Если А(х), то В(х)». Противоположное ему предложение: «Если не-А(х), то не-В(х)».

Предложение, обратное противоположному: «Если не-В(х), то не-А(х)».

Символически предложение, обратное противоположному, запишем так:

не-В(х) > не-А(х).

Таблица 5 — Предложение, обратное противоположному.

Упражнение. Известно следующее:

Если Соня выходит из дома, то она выключает телевизор.

Постройте предложение, обратное противоположному.

Решение. Предложение, обратное противоположному: Если Соня не выключает телевизор, то она не выходит из дома.

Вопросы: Верно ли оно? (Да, верно). Почему?

2. Материал для занятия «Равносильность и следование».

Определение. Предложения б (х) и в (х) называются равносильными, если для любого значения переменной x эти предложения одновременно превращаются, либо в истинные высказывания, либо в ложные высказывания.

Вопросы и ответы.

а) Вопрос: Предложения «x2 = 4» и «|x| = 2» равносильны? (Ответ: Да.).

б) Вопрос: Предложения «x2 = 4» и «x = 2» равносильны? (Ответ: Нет.) Вопрос: Почему? (Ответ: Потому что при x = -2 предложение «x2 = 4» принимает значение истина, а предложение «x = 2» — значение ложь.).

Докажем утверждение.

Утверждение 1. Для любых предложений А(х) и В(х) равносильны предложения «Если А(х), то В(х)» и «Если не-В(х), то не-А(х)».

Методический комментарий. Следует особо отметить, что указанные предложения равносильны независимо от содержания предложений А(х) и В(х). Поэтому говорят, что предложения «Если А(х), то В(х)» и «Если не-В(х), то неА(х)» логически равносильны, и записывают так: А(х) > В(х) ??B(х) > A(х).

Доказательство. Пусть А(х) и В(х) — произвольные предложения. И пусть x0 — произвольный элемент из М.

Составим таблицу истинности для предложений «Если А(х0), то В(х0)» и «Если не-В(х0), то не-А(х0)».

Таблица 6 — Таблица истинности для доказательства равносильности предложений.

Как видим, два последних столбца таблицы 6 совпадают. Итак, мы доказали, что предложения «Если А(х), то В(х)» и «Если не-В(х), то не-А(х)» равносильны. ?

Проводя математические рассуждения, часто используют слово «следует». Уточним, что значит «из одного предложения следует другое». Определение. Пусть б (х) и в (х) — произвольные предложения с переменной, которой можно придавать значения из множества М. Будем говорить, что из предложения б (х) следует предложение в (х), и писать б (х)?в (х) тогда и только тогда, когда для любого а из множества М истинна импликация б (а) > в (а).

Если из предложения б (х) следует предложение в (х) то будем говорить также: «Предложение в (х) следует из предложения б (х)» или «Предложение в (х) является следствием предложения б (х)».

Вопросы и ответы.

а) Вопрос: Из предложения «x = 2» следует предложение «x2 = 4»? (Ответ: Да.) б) Вопрос: Из предложения «x2 = 4» следует предложение «x=2»? (Ответ: Нет.) Вопрос: Почему? (Ответ: Потому что при x = -2 предложение «x2 = 4» принимает значение истина, а предложение «x = 2» — значение ложь. А значит, импли;

кация ложна.).

Вопросы и ответы.

а) Вопрос: Если б (х)?в (х) и верно б (x), то что можно сказать про в (x)? (Ответ: в (x) тоже верно.).

б) Вопрос: Если известно, что верно б (x) и не является верным в (x), то верно, что из б (х) следует в (х)? (Ответ: нет, из б (х) не следует в (х).).

Символически можно записать это так: б (х) ? в (х).

Упражнение. Докажите следующее утверждение:

Утверждение 2. Для любых предложений A и B эти предложения равносильны, тогда и только тогда, когда из A следует B и из B следует A.

Можно записать так: А ??В тогда и только тогда, когда А ??В и В ??А.

Таким образом, поскольку для любых предложений А и В: предложения.

«Если А, то В» и «Если не-В, то не-А» равносильны, то из предложения «Если А, то В» следует предложение «Если не-В, то не-А».

Символически будем записывать так: А > В B > A.

Замечание. Поскольку из предложения А > В следует предложение.

B > A для любых предложений А и В, независимо от содержания, то говорят, что из А > В логически следует B > A.

Пример. Из предложений А, А>В логически следует предложение B (А, А>В B).

3. Материал для занятия «Индуктивные и дедуктивные рассуждения».

Умение правильно рассуждать — это отличительная черта разумного образованного человека. Поэтому каждому необходимо этому научиться. Особенно это умение важно для занятий математикой.

Индуктивное рассуждение (от лат. inductio — «наведение») — это рассуждение, в котором связь посылок и заключения не опирается на логический закон, в силу чего заключение вытекает из принятых посылок не с логической необходимостью, а только с некоторой вероятностью. При индуктивном рассуждении из истинных посылок можно получить ложное заключение.

Дедуктивное рассуждение (от лат. deductio — «выведение») — рассуждение, в котором переход от посылок к заключению опирается на логический закон, в силу чего заключение с логической необходимостью следует из принятых посылок. Характерная особенность дедукции заключается в том, что от истинных посылок она всегда ведёт только к истинному заключению. Дедуктивные рассуждения будем называть также логически правильными или просто правильными рассуждениями.

Математика — наука дедуктивная. Это означает, что основным методом обоснования знаний в математика является выведение одних утверждений из других. Причём это выведение происходит по чётким правилам, обеспечивающим достоверность выводов при условии, что исходные утверждения были достоверными. Это отличает математику от других наук, в которых широко используются индуктивные рассуждения и такие методы, как эксперимент, наблюдение и т. п.

Справедливыми в математике признают только те утверждения, которые обоснованы с помощью дедуктивных рассуждений. Все интуитивно полученные в процессе математического творчества результаты, сформулированные в виде утверждений, затем обязательно обосновывают с помощью дедуктивных рассуждений.

Вопросы и ответы.

а) Если лёд нагревать, он тает. Лёд нагревают. Следовательно, лёд тает.

Вопрос: Это рассуждение дедуктивное или индуктивное? (Ответ: Дедуктивное.) Вопрос: Почему? (Ответ: Потому что А, А > В ??B.).

б) Италия — республика. Португалия — республика. Финляндия — республика. Франция — республика. Италия, Португалия, Финляндия, Франция западноевропейские страны. Следовательно, все западноевропейские страны являются республиками.

Вопрос: Посылки в этом рассуждении истинны или ложны? (Ответ: Истинны.) Вопрос: А заключение в этом рассуждении истинно или ложно? (Ответ: Ложно.).

Вопрос: Почему? (Ответ: Потому что среди западноевропейских стран имеются не только республики, но и монархии, например, Великобритания.).

Вопрос: Данное рассуждение дедуктивное или индуктивное? (Ответ: Индуктивное.).

в) Канада — республика. США — республика. Канада и США — североамериканские государства. Следовательно, все североамериканские государства являются республиками.

Вопрос: Посылки в этом рассуждении истинны или ложны? (Ответ: Истинны.) Вопрос: А заключение в этом рассуждении истинно или ложно? (Ответ: Истинно.).

Вопрос: Данное рассуждение дедуктивное или индуктивное? (Ответ: Индуктивное.).

Индуктивные рассуждения опираются на некоторые фактические или психологические основания. В таком рассуждении заключение может содержать информацию, отсутствующую в посылках. Поэтому достоверность посылок не гарантирует достоверности выведенного из них заключения.

Дедукция не сводится к переходу от общего к частному, а индукция — к переходу от частного к общему. Дедукция — это выведение заключений, столь же достоверных, как и принятые посылки, индукция — выведение вероятных (правдоподобных) заключений.

4. Материал для занятия «Задачи на распознавание следствий».

Задача 1. Дано верное предложение: «Когда Семён Витальевич на рыбалке ловит рыбу, он переводит свой телефон на беззвучный режим». Выберите предложения, которые следуют из данного предложения. Ответ обоснуйте.

• 1) Если Семён Витальевич находится на карповой рыбалке, то его телефон на беззвучном режиме.
• 2) Если телефон Семёна Витальевича не на беззвучном режиме, то он не ловит рыбу. 3) Если телефон Семёна Витальевича на беззвучном режиме, то он ловит рыбу.
• 4) Если Семён Витальевич не ловит рыбу, то его телефон не на беззвучном режиме. Решение. Запишем данное предложение в форме «Если …, то …»: «Если С. В. на рыбалке ловит рыбу, то он обязательно переводит свой телефон на беззвучный режим».

Обозначим буквой А предложение «С.В. ловит рыбу на рыбалке», буквой В — «он (С.В.) обязательно переводит свой телефон на беззвучный режим». Тогда данное предложение можно символически записать так: А > В.

1) Если С. В. находится на карповой рыбалке, то его телефон на беззвучном режиме. Выявим форму этого предложения. Обозначим через С — предложение «С.В. находится на карповой рыбалке». Тогда предложение (1) запишем символически так: С > В.

Из предложений С > А и А > В следует предложение С > В.

Очевидно, предложение С > А верно, потому что карповая рыбалка — это одна из разновидностей рыбалки.

Следовательно, предложение (1) следует из данного предложения. Согласно условию, верно предложение А > В. Значит, поскольку верны предложения С > А и А > В, а предложение С > В из них следует, то верно и само предложение (1) С > В.

2) Если телефон С.В. не на беззвучном режиме, то он не ловит рыбу.

Предложение (2) символически запишем так: В > А. Оно является предложением, обратным противоположному для предложения А > В. Предложение (2) логически следует из данного предложения, в силу равносильности данного предложения и предложения, обратного противоположному.

3) Если телефон С.В. на беззвучном режиме, то он ловит рыбу.

Предложение (3) символически запишем так: В > А. Оно является предложением, обратным данному А > В. Но обратное предложение логически не следует из данного предложения. Таким образом, предложение (3) не следует из данного предложения.

4) Если С. В. не ловит рыбу, то его телефон не на беззвучном режиме.

Предложение (4) символически запишем так: А > В. Оно является предложением, противоположным данному А > В. Но противоположное предложение не следует из данного предложения. Таким образом, предложение (4) не следует из данного предложения.

Ответ: 1, 2.

Задача 2. Определитель квадратной матрицы, у которой первые две строки пропорциональны, равен нулю. Выберите предложения, которые из этого следуют, и объясните почему.

• 1) Если определитель квадратной матрицы равен нулю, то у этой матрицы первые две строки пропорциональны.
• 2) Если первые две строки квадратной матрицы пропорциональны с коэффициентом 2, то её определитель равен нулю.
• 3) Если первые две строки квадратной матрицы не пропорциональны, то её определитель не равен нулю.
• 4) Если определитель квадратной матрицы не равен нулю, то у этой матрицы первые две строки не пропорциональны.

Решение. Запишем в условной форме данное предложение: «Если первые две строки квадратной матрицы пропорциональны, то её определитель равен нулю». Не будем вникать в содержание данного предложения. Обозначим через А предложение «первые две строки квадратной матрицы пропорциональны». Обозначим через В предложение «определитель квадратной матрицы равен нулю».

Символически запишем его так: А > В.

1) Если определитель квадратной матрицы равен нулю, то у этой матрицы первые две строки пропорциональны.

Предложение (1) символически запишем так: В > А. Оно является предложением, обратным данному А > В. Но обратное предложение логически не следует из данного предложения. Таким образом, предложение (1) не следует из данного предложения.

2) Если первые две строки квадратной матрицы пропорциональны с коэффициентом 2, то её определитель равен нулю.

Предложение (2) запишем так: С > В, где С — первые две строки квадратной матрицы пропорциональны с коэффициентом 2. Очевидно, С > А. Из предложений С > А и А > В следует предложение С > В. Следовательно, предложение (2) следует из данного предложения.

3) Если первые две строки квадратной матрицы не пропорциональны, то её определитель не равен нулю.

Предложение (3) символически запишем так: А > В. Оно является предложением, противоположным данному А > В. Предложение (3) символически запишем так: А > В. Оно является предложением, противоположным данному А > В. Но противоположное предложение не следует из данного предложения. Таким образом, предложение (3) не следует из данного предложения.

4) Если определитель квадратной матрицы не равен нулю, то у этой матрицы первые две строки не пропорциональны.

Предложение (4) символически запишем так: В > А. Оно является предложением, обратным противоположному для предложения А > В, а значит, является его следствием.

Ответ: 2, 4.

6. Домашние задания Решения задач, предназначенных для домашней работы, приводятся в Приложении 2.

I. Домашнее задание по теме «Обратное, противоположное и обратное противоположному предложения для данного».

Задание 1. Для каждого из приведённых ниже предложений перейдите к условной форме и затем выделите посылку и заключение:

а) В равностороннем треугольнике все углы равны.

б) Вертикальные углы — равны.

в) Углы при основании равнобедренного треугольника равны.

Задание 2. Для предложения «Если В(х), то А(х)» постройте предложение, противоположное обратному.

Решение. Данное предложение: Если В(х), то А(х)".

Обратное предложение: Если А(х), то В(х)". Противоположное обратному: Если не-А(х), то не-В(х)".

II. Домашнее задание по теме «Равносильность и следование».

Задание 1. Докажите, что для любых предложений А(х), то В(х) равносильны предложения «Если В(х), то А(х)» и «Если не-А(х), то не-В(х)».

Указание. Составьте таблицу истинности.

Задание 2. Постройте для данного предложения обратное, противоположное и обратное противоположному. Какие из них являются верными? Следствиями данного?

а) Если идёт дождь, то земля мокрая.

б) Если мама уезжает в командировку, то Маша уезжает жить к бабушке.

в) Если два числа являются нечётными, то их сумма — чётное число.

III. Домашнее задание по теме «Задачи на распознавание следствий».

Задание 1. Дано предложение «Произведение любых трёх последовательных натуральных чисел делится на 6».

1) Выясните, какое из приведённых предложений является обратным, какое — противоположным, а какое — обратным противоположному для данного предложения. 2) Установите, какие из них являются следствиями данного предложения. 3) Обоснуйте ответы.

а) Если произведение трёх натуральных чисел не делится на 6, то они не идут друг за другом.

б) Если произведение трёх натуральных чисел делится на 6, то они идут друг за другом.

в) Если три натуральных числа не идут друг за другом, то их произведение не делится на 6.

Задание 2. В жилых домах, в которых больше 12 этажей, установлены электрические плиты вместо газовых. Выберите предложения, которые следуют из данного предложения и объясните почему.

• 1) Если в доме установлены электрические плиты, то в этом доме больше 12 этажей.
• 2) Если в доме больше 12 этажей, то в нём установлены электрические плиты.
• 3) Если в доме не более 12 этажей, то в нём установлены газовые плиты.
• 4) Если в доме установлены газовые плиты, то в этом доме менее 13 этажей.

Методические рекомендации Мы разработали методические рекомендации по проведению курса «Дедуктивные рассуждения в математике».

• 1. Для распознавания, является ли правильным рассуждение, рекомендуем выявить его логическое строение.
• 2. В курсе задачи на распознавание правильных рассуждений должны занимать центральное место. Изучение дедуктивных рассуждений рекомендуем начать с задач на распознавание следствий, которые являются важным частным случаем задач на распознавание дедуктивных рассуждений.
• 3. При изучении темы «Равносильность и следование» рекомендуем дать определения равносильности и следования, но не давать определения логической равносильности и логического следования, поскольку они существенно сложнее. Понятия логической равносильности и логического следования использовать можно, но не давать их определения, а только пояснять на примерах. Важно отметить, что соответствующие утверждения о равносильности верны для любых предложений, независимо от их содержания.
• 4. На первом занятии целесообразно провести диагностическую (проверочную) работу, чтобы определить уровень логических знаний и умений учащихся. А также следует провести проверочную работу после завершения изучения второго (основного) раздела для установления, насколько усвоен основной материал курса. Варианты работ представлены в разделе 2.4. А в конце курса желательно провести контрольную работу для проверки усвоения всего материала курса.
• 5. Отметим, что в задачах логического характера (на распознавание следствий) из ЕГЭ по математике обоснование ответа не требуется, а необходимо только указать правильный ответ (выбрать предложения из списка). Считаем, что обучение решать такие задачи подразумевает обучение не только указывать правильный ответ, но и обосновывать его. Предлагаемая нами методика обучения решению таких задач основана на использовании средств логики.

Методические рекомендации по обучению распознаванию дедуктивных рассуждений, специфические для нашей методики:

• 1. Если посылки и заключение в рассуждении сформулированы в безусловной форме, то рекомендуется перейти к условной форме «Если …, то …».
• 2. Ввести обозначения элементарных предложений.
• 3. Выявить форму (логическую структуру) посылок и заключения данного рассуждения и записать их символически.
• 4. Записать символически схему рассуждения.
• 5. Проанализировать полученную схему: выяснить, гарантирует ли она истинность заключения при истинных посылках. Для обоснования отрицательного ответа нужно привести пример рассуждения по этой же схеме, посылки которого истинны, а заключение ложно.
• 6. Сделать вывод на основании п.5: является ли это рассуждение правильным или неправильным.

Результаты опытно-экспериментальной проверки Опытно-экспериментальная проверка проходила в 2016;17 уч. г. и была разбита на три этапа: констатирующий; поисковый; обучающий и контролирующий.

Первый этап. Цель этого этапа — анализ учебной и методической литературы по теме исследования, изучение состояния математических курсов по выбору в девятых классах. На данном этапе использовались следующие методы: посещение уроков по математике, наблюдение за учащимися, беседы с учащимися и учителями.

Второй этап. Цель этого этапа — поиск и анализ разработанных курсов по выбору по данной теме, отбор материала для собственного курса и его разработка. На данном этапе осуществлялся поиск, отбор материалов для содержания курса по выбору. Нами были разработаны и скорректированы учебнометодические материалы для курса по выбору: программа курса, набор задач, методические рекомендации, материалы для занятий по некоторым темам.

Третий этап проходил на базе ГБОУ «Школа с углублённым изучением английского языка № 1359 им. авиаконструктора М.Л. Миля» г. Москвы в феврале 2017 года. В опытно-экспериментальной проверке участвовали 26 учеников 9 класса.

На третьем этапе опытно-экспериментальной проверки были проведены занятия по разработанным материалам для курса по выбору «Дедуктивные рассуждения в математике», представленным в разделе 2.3, по следующим темам:

• 1. Обратное, противоположное и обратное противоположному предложения.
• 2. Равносильность и следование.
• 3. Задачи на распознавание следствий.

На занятиях с учащимся был изучен теоретический логический материал по данным темам, позволяющий сделать правильный выбор (дать правильный ответ) и обосновать ответ.

Перед началом проведения занятий курса по выбору «Дедуктивные рассуждения в математике» учащимся была предложена проверочная работа № 1 с целью диагностики умения учащихся решать задачи из ЕГЭ по математике базового уровня только на основе логической интуиции, здравого смысла. Было разработано три варианта работы № 1. В каждом варианте предложены три задачи с разным содержанием. Первые две задачи представляют собой фрагменты задачи из ЕГЭ, а третья задача аналогична задачам из ЕГЭ. В первом задании каждого варианта предлагаются задачи с одним и тем же заданием и нематематическим сюжетом, с одинаковым условием А > В, различными заключениями (для выяснения следствия) в каждом варианте по следующим схемам:

В > А, А > В, В > А. Во втором задании каждого варианта предлагаются задачи с одним и тем же заданием и математическим сюжетом (отличным от сюжета первой задачи), с одинаковым условием А > В, различными заключениями (для выяснения следствия) в каждом варианте по следующим схемам:

В > А, А > В, В > А. Первая и вторая задача отличаются друг от друга тем, что схемы в вариантах не повторяются. В третьем задании представлены задачи на выбор следствий данного предложения (из четырёх предложенных вариантов ответов два верных и два неверных предложения). Исходное предложение в задаче № 3 для всех вариантов одинаковое, но отличаются они друг от друга порядком предложений, предлагаемых на выбор. В таблице 7 отражена структура предложений на выбор в проверочной работе № 1.

Таблица 7 — Структура предложений на выбор в проверочной работе № 1.

Приведём в качестве примера первый вариант проверочной работы № 1.

Вариант 1.

Задача 1. Известно: Если какая-нибудь кошка идёт по забору, собака Шарик, живущая в будке возле дома, обязательно лает. Выясните, является ли следствием данного предложения следующее предложение, и обоснуйте ответ:

«Если Шарик лает, значит, по забору идёт кошка».

Задача 2. Дано предложение: «Если число делится на 8, то оно делится на 4».

Выясните, является ли следствием данного предложения следующее предложение, и обоснуйте ответ:

«Если число не делится на 8, то оно не делится на 4».

Задача 3. Согласно градостроительным нормам, в домах выше 5 этажей должен быть установлен лифт. Считая, что эти нормы неукоснительно исполняются, выберите предложения, которые непосредственно из этого следуют:

а) Если в доме нет лифта, то он не выше 5 этажей. б) Если в доме менее 6 этажей, то в нём лифта нет. в) Если в доме больше 5 этажей, то в нём есть лифт. г) Если в доме есть лифт, то он выше 5 этажей.

За первые два задания ученик мог получить максимум 3 балла, за третье задание — максимум 4 балла. За всю работу — максимум 10 баллов.

Для оценки результатов практической работы нами были разработаны и использованы следующие критерии, отражённые в таблице 8.

Таблица 8 — Критерии оценивания проверочной работы № 1.

В написании проверочной работы № 1 приняли участие 26 обучающихся. Приведём и проанализируем результаты проверочной работы № 1. В таблице 9 для каждого из трех заданий отражено количество учащихся (в процентах), получивших 0, 1, 2, 3 и 4 балла.

Таблица 9 — Результаты выполнения заданий проверочной работы № 1 (в %).

Результаты показывают, что за первые две задания никто из учащихся не набрал максимальное количество баллов, поскольку учащиеся испытывали трудности с обоснованием ответов. Это можно было предположить заранее. При выполнении этих заданий большинство учащихся давало обоснования, опираясь на здравый смысл и математические знания. Результаты за два первых задания, представленные в таблице 9, показывают, что учащиеся лучше справились со вторым заданием (с математическим сюжетом).

В третьем задании максимальное количество баллов получили 27% учащихся (обосновывать свой выбор не требовалось). При выполнении этого задания большинство учащихся выбрало два верных варианта и один неверный.

Таблица 10 — Результаты выполнения проверочной работы № 1 (в %).

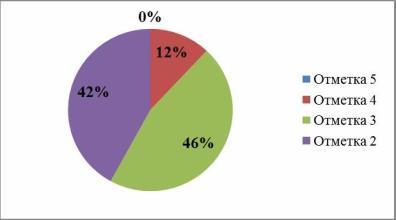
Рис. 1 — Результаты проверочной работы № 1

Анализ приведённых результатов позволяет сделать вывод, что большинство учащихся при решении первых двух задач, опираясь только на логическую интуицию, дают правильный ответ и почти без обоснований. Из-за того, что в ответах учащихся не было верных обоснований, они не смогли набрать максимальное количество баллов. При решении третьей задачи большинство учащихся выбирало вместе с верными ответами и неверный. На максимальный балл это задание удалось выполнить малому количеству учащихся (27%). Однако не всем из этих 27% учащихся удалось успешно справиться с работой, а только 12%.

После проведения проверочной работы № 1 учащимся была предложена следующая анкета:

Анкета № 1 (обведите кружочком нужный пункт).

1. Как вы относитесь к доказательствам (математическим рассуждениям)?

a) понимаю доказательства.

b) мне интересно изучать доказательства.

c) с трудом понимаю доказательства.

d) не понимаю доказательства совсем.

e) доказательства мне не интересны.

f) заучиваю доказательства без понимания.

2. Интересны ли Вам задачи на рассуждения (выведения следствий, распознавания следствий)?

a) да, интересны b) нет, не интересны.

3. Хотите ли Вы научиться отличать правильные и неправильные рассуждения (выбирать следствия исходного предложения из предложенных вариантов)?

a) да, хочу b) нет, не хочу c) не знаю.

4. Хочу научиться распознавать следствия из данного предложения и распознавать правильные рассуждения потому, что это:

a) поможет решать задания такого типа на ЕГЭ.

b) поможет развить логическое мышление.

c) поможет разбираться в доказательствах при изучении геометрии.

d) просто интересно.

5. Хотите ли вы научиться правильно рассуждать?

a) да, хочу. b) нет, не хочу Первое анкетирование проведено с целью наличия интереса учащихся к доказательствам (математическим рассуждениям) до начала изучения курса по выбору. Анкетированием было охвачено 26 учащихся. Приведём его результаты. Ниже, в таблице 11, указано количество учащихся (в процентах), выбравших тот или иной вариант ответа на каждый из пяти вопросов.

Таблица 11 — Количество учащихся (в %), выбравших тот или иной вариант ответа анкеты № 1.

Анализ результатов проведённого анкетирования показал, что большинство учащихся считают, что понимают доказательства (38,5%) и им интересно их изучать (38,5%), что им интересны задачи на рассуждения (85%). Большинство учащихся хочет научиться отличать правильные и неправильные рассуждения (92%), а также правильно рассуждать, потому что это поможет развить их логическое мышление (72%).

В ходе третьего этапа опытно-экспериментальной проверки, с целью контроля усвоения учащимися изученного материала, точнее, умения применять изученный материал при решении задач из ЕГЭ по математике базового уровня на выведение следствий, была проведена проверочная работа № 2. Для нее, как и для проверочной работы № 1, было разработано три варианта. В каждом из них предложены три задачи с различными сюжетами, которые отличны от сюжетов задач в работе № 1. По структуре проверочные работы № 1 и № 2 совпадают, т. е. первая задача с нематематическим содержанием, вторая задача с математическим содержанием, а третья — одинаковая в каждом варианте, различие только в порядке предлагаемых ответов. В работе содержатся предложения, построенные по следующим схемам: А > В, В > А, А > В, В > А. Структура предложений в ответах проверочной работы № 2 аналогична той, что была в проверочной работе № 1 (таблица 7).

Приведём в качестве примера второй вариант проверочной работы № 2.

Вариант 2.

Задача 1. Известно: Когда учитель математики Иван Петрович ведёт урок, он обязательно отключает свой телефон. Выясните, является ли следствием данного предложения следующее предложение, и обоснуйте ответ:

«Если Иван Петрович не ведёт урок, то его телефон включён».

Задача 2. Дано предложение: «Если сумма цифр натурального числа делится на 3, то это число делится на 3».

Выясните, является ли следствием данного предложения следующее предложение, и обоснуйте ответ:

«Если натуральное число не делится на 3, то сумма его цифр не делится на 3». Задача 3. В офисе фирмы компьютеры работают только от сетевого электропитания. Если компьютеры работают, то электричество в офисе есть. Выберите предложения, которые непосредственно из этого следуют, и обоснуйте ответ.

а) Если в офисе нет электричества, то не работает компьютер директора.

б) Если компьютеры не работают, то в офисе нет электричества.

в) Если в офисе нет электричества, то компьютеры не работают.

г) Если в офисе есть электричество, то компьютеры работают.

Для оценки проверочной работы № 2 использовали те же критерии, что и для проверочной работы № 1 (таблица 8), только для оценки задания 3 были внесены изменения, представленные в таблице 12.

Таблица 12 — Критерий оценивания задания 3 проверочной работы № 2.

Приведём и проанализируем результаты проверочной работы № 2.

В таблице 13 для каждого из трех заданий отражено количество учащихся (в процентах), получивших 0, 1, 2, 3, 4 и 5 баллов.

Таблица 13 — Результаты выполнения заданий проверочной работы № 2 (в %).

Результаты показывают, что максимальное количество баллов за первые два задания получили 61,5% учащихся, а за третье — 31% учащихся.

Результаты проверочной работы № 2, переведённые в пятибалльную систему, представлены в таблице 14 и диаграмме (рис. 2).

Таблица 14 — Результаты выполнения проверочной работы № 2 (в %).

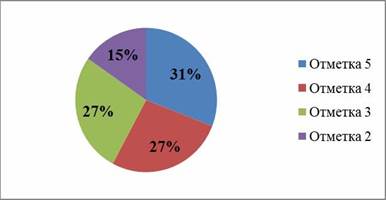
Рис. 2 — Результаты проверочной работы № 2

На диаграмме (рис. 3) показано количество учеников, получивших данное количество баллов за проверочные работы № 1 и № 2.

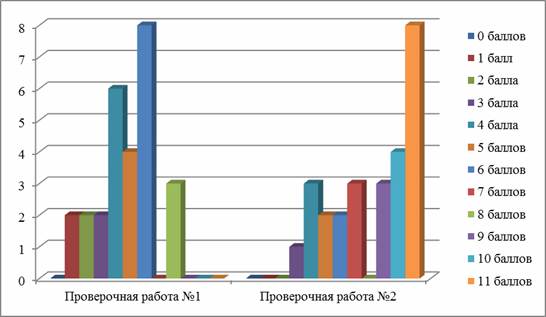
Рис. 3 — Результаты (в баллах) проверочных работ № 1 и № 2

На диаграммах (рис. 4, рис. 5) показаны результаты выполнения проверочных работ № 1 и № 2.

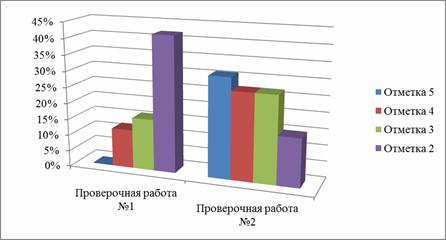
Рис. 4 — Результаты выполнения (в %) проверочных работ № 1 и № 2

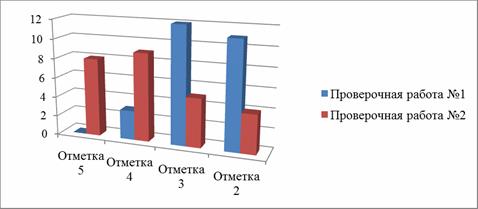
Рис. 5 — Результаты выполнения проверочных работ № 1 и № 2

Анализ приведённых результатов позволяет сделать вывод о достаточно хорошем уровне усвоения учащимися изученного материала, а также о его доступности для учащихся.

После проведённых занятий (в конце последнего занятия) было проведено второе анкетирование. Целью этого анкетирования было выявление интереса к изложенному материалу, мнения учащихся о доступности логического материала с дифференциацией по темам.

Анкета № 2.

1. Интересно ли Вам было решать задачи на распознавание следствий из данных условий (на распознавание правильных рассуждений)?

a) да, интересно; b) нет, не интересно; c) не знаю.

2. Выделите в списке то, что было для Вас самым интересным (совсем неинтересным) при изучении курса? (Интересное отметьте знаком +, неинтересное отметьте знаком -).

a) изучение теории: определения импликации, логического следствия данного предложения, логической равносильности предложений, доказательство равносильности предложений;

b) построение обратного, противоположного и обратного противоположному предложений для данного предложения;

c) выявление логических взаимосвязей между данным предложением, обратным ему, противоположным ему и обратным противоположному;

d) решение задач на выявление следствий из данных условий с применением полученных логических знаний.

3. Выделите в списке то, что было для Вас самым трудным (легким) на занятиях? (напишите слова трудно и легко, где считаете нужным).

a) изучение теории: определение импликации, логического следствия данного предложения, логической равносильности предложений, доказательство равносильности;

b) построение обратного, противоположного и обратного противоположному предложений для данного предложения;

c) выявление логических взаимосвязей между данным предложением, обратным ему, противоположным ему и обратным противоположному;

d) решение задач на выявление следствий из данных условий с применением полученных логических знаний.

• 4. Помогли ли Вам полученные логические знания
• а) при решении задач на выявление следствий из данных условий?
• 1) да; 2) нет; 3) не знаю.

b) при обосновании ответа задач на выявление следствий из данных условий?

• 1) да; 2) нет; 3) не знаю.
• 5. Хотите ли Вы продолжить учиться правильно рассуждать?

a) да, хочу; b) нет, не хочу; c) не знаю.

В таблицах 15 и 16 отражены результаты анкетирования.

Таблица 15 — Результаты анкеты № 2 (вопросы 1−3 и 5).

Общее количество процентов в вопросах 2 и 3 (на выявление мнения учащихся) выше 100%, а в одном вопросе ниже 100%. Это связано с тем, что некоторые ученики отмечали несколько вариантов ответа или вообще ничего не отмечали.

Таблица 16 — Результаты анкеты № 2 на вопросы 4а и 4b.

Анализ результатов проведённого анкетирования показал, что учащимся было интересно решать задачи на распознавания следствий из данных условий (81%).Для учащихся интересным при изучении курса было решение задач на выявление следствий из данных условий с применением полученных логических знаний (77%). Лёгким на занятиях для них было построение обратного, противоположного и обратного противоположному предложений для данного предложения (73%). Не интересным при изучении курса (35%) и самым трудным (50%) на занятиях было изучение теории. Полученные логические знания помогли учащимся при решении задач на выявление следствий из данных условий (88,5%) и при обосновании ответа (77%), что видно по результатам проверочной работы № 2 (таблица 14 и рис. 2). Учащимся понравились занятия курса по выбору «Дедуктивные рассуждения в математике», и они хотели бы продолжить учиться правильно рассуждать (81%).

Выводы. Учащиеся успешно справились с проверочной работой № 2. Несмотря на то, что проведено было всего лишь три занятия, 30,9% учеников получили отметку «5», 26,9% учеников получили отметку «4». Таким образом, большинство учащихся (57,8%) справилось с предложенными задачами на отметки «4» и «5».

У учащихся повысилась способность решать задачи на выведение следствий из ЕГЭ по математике базового уровня, а значит, и в целом повысилась способность правильно рассуждать. Из полученных результатов можно сделать вывод, что предложенный нами материал интересен и доступен учащимся. А значит, способствует повышению познавательной активности и интереса к логическим вопросам.

Предложенный нами курс по выбору полезен для учащихся 9-х классов, потому что ученики показали хорошие результаты, и как показало анкетирование, полученные знания им помогли при решении задач на выведение следствий. Цели опытно-экспериментальной проверки достигнуты.