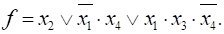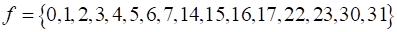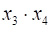Минимизация ФАЛ с помощью карт Карно

Так как одна и та же ФАЛ может быть записана с помощью различных формул, то возникает задача получения минимальной формы записи (с минимальным числом букв), которая потребует минимальных затрат аппаратуры при реализации.

Рассмотрим процесс минимизации ФАЛ с помощью карт Карно. Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более шести. Карта Карно (рис. 10) является другой формой представления таблицы истинности (табл. 5). Каждая клетка карты соответствует строке таблицы (двоичному набору). Часть клеток (половина), которым соответствует значение xi = 1, отмечается чертой. Соответственно в областях, не обозначенных чертой, переменная xi = 0.

Таблица 5.

Таблица истинности.

Для задания ФАЛ в карте Карно надо проставить 1 в тех клетках, которые соответствуют разрешенным наборам. В карте на рис. 10 задана ФАЛ из табл. 5.

Минимизация ФАЛ по карте Карно заключается в объединении соседних клеток в прямоугольные контуры, причем соседними считаются и клетки, разделенные внешней границей карты.

Минимизация производится по следующим правилам.

Все единицы должны быть включены в прямоугольные контуры.

Во всех клетках контура должны стоять единицы.

Число клеток в контуре должно быть кратным степени числа 2: 1, 2, 4, 8, … .

Контуры могут накладываться друг на друга.

Контуры, все клетки которых уже вошли в другие контуры, являются лишними.

Для получения наиболее простой формулы надо выбирать контуры с максимальным числом клеток.

Каждому контуру соответствует конъюнкция, составленная из переменных, значения которых не изменяются во всех клетках контура.

Конъюнкции контуров объединяются знаками дизъюнкции.

Ниже представлена ФАЛ, соответствующая карте Карно на рис. 10:

Минимизируем функцию, представленную своими разрешёнными наборами, с использованием карт Карно (рис. 11):

.

В карте Карно от пяти переменных два контура, удовлетворяющие указанным правилам, объединяются в один контур, если они расположены симметрично относительно центральной оси. Например, контур на рис. 11, соответствующий конъюнкции .

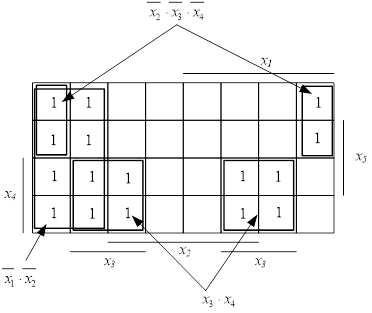
Рис. 11. Минимизация по карте Карно

В итоге мы получаем следующую функцию: