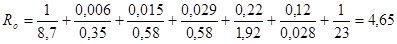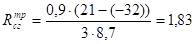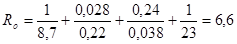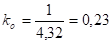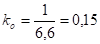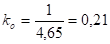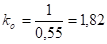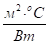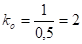Определение сопротивления теплопередаче перекрытия здания

На рисунке 3.3 показана конструкция кровли.

В таблице 3.4 приведены данные для определения требуемого сопротивления теплопередаче и из условий энергосбережения.

Таблица 3.4. Исходные данные для расчета.

n	tвн	tн.в	tн	в
;	оС.	оС.	оС.	Вт/(м2· оС).	оС.	сут.
0,9.		— 32.		8,7.	— 4.

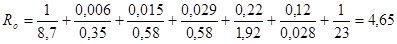
Рисунок 3.3. Конструкция кровли Требуемое сопротивление теплопередаче перекрытия по санитарно-гигиеническим условиям определим по формуле (3.1):

.

Требуемое сопротивление теплопередаче перекрытия в зависимости от градусо-суток определим по формуле (3.2):

.

Общее фактическое сопротивление теплопередаче для всех слоев ограждения определим по формуле (3.3):

.

Определение коэффициентов теплопередачи ограждающих конструкций

Определим значения коэффициентов теплопередачи наружных и внутренних стен, чердачного перекрытия, пола первого этажа, оконных и дверных проемов по формуле (3.4):

.

Наружные стены:

.

Чердачное перекрытие:

.

Пол первого этажа:

.

Тройное окно в раздельно-спаренных переплетах:

.

где R_o=0,55 при тройном остеклении в деревянных раздельно-спаренных переплетах принимается согласно [3].

Дверные проемы:

.

где R_o=0,5 для наружных двойных деревянных дверей принимается согласно [3].