Лекция 1. Кинематика точки

Кинематика изучает движение тел по отношению к системам координат, связанных с другими телами (например, с Землей) с геометрической стороны, без учета причин, вызывающих это движение. При этом движение тел предполагается совершающимся во времени.

Для простоты изучения, в кинематике изучается сначала движение одной точки, а затем — движение твердых тел.

Но прежде чем приступить к изучению кинематики точки, рассмотрим понятие производной вектора по скалярному аргументу.

Переменный вектор и его производная по скалярному аргументу

Если каждому значению независимого скалярного переменного u в интервале b < u < c соответствует определенный вектор, то будем говорить, что вектор есть непрерывная функция скалярного переменного u:

. (1.1).

Если вектор при своем изменении сохраняет одно и тоже начало (пусть точка О) (рис. 5.1), то уравнение (5.1) определяет движение его конца. Кривая, которую описывает конец вектора называется годографом переменного вектора.

кинематика точка движение твердое тело Пусть u некоторое фиксированное значение аргумента вектора, u — его приращение, тогда при значении.

u +u — будем иметь другой вектор .

Разность называется приращением вектора .

Предел отношения.

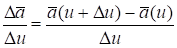
при u 0, если он существует, называется производной вектора по скалярному аргументу u и обозначается.

.

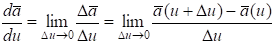
Вектор всегда направлен по секущей (рис. 5.1). При 0 секущая займет предельное положение, совпадающее с касательной к годографу вектора. Следовательно, производная вектора по скалярному аргументу всегда направлена по касательной к годографу этого вектора.

Свойства производной вектора по скалярному аргументу

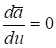
1., если .

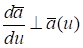
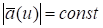
2., если ,.

т.е. изменяется только направление вектора в пространстве. Годограф при этом находится на поверхности сферы, а касательная к сфере перпендикулярна ее радиусу.

3. .

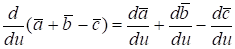
4. ,.

где — скалярный коэффициент.

5. .

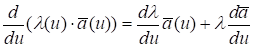
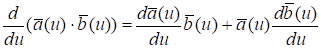
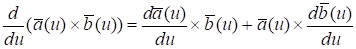
6. .

Пусть вектор задан в неподвижной прямоугольной системе координат, (рис. 1.2).

Тогда.

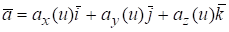
(1.2).

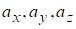
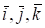
где — проекции вектора на координатные оси, а — орты этих осей.

Так как — постоянные векторы.

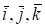
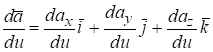
. (1.3).

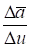
С другой стороны, вектор можно также записать через его проекции.

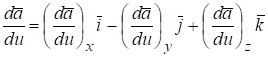
. (1.4).

Сравнивая формулы (5.3) и (5.4), получим:

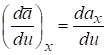
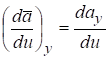
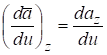
,. (1.5).

Таким образом, доказали:

Проекция производной вектора на неподвижное направление равна производной от проекции вектора на соответствующее направление.

Перейдем к изучению кинематики точки.

Основные задачи кинематики точки

Кинематика точки рассматривает две основные задачи.

• А). Задача задания движения точки. Движение точки в пространстве считается заданным, если найден способ, при помощи которого каждому моменту времени t однозначно ставится в соответствие положение точки в пространстве.
• Б). Задача определения кинематических характеристик движения точки — скорости точки и ускорения точки.

Существует три способа задания движения точки: векторный, координатный и естественный.

Векторный способ задания движения точки

Рассмотрим движение материальной точки М относительно некоторого тела, которое считается неподвижным. Пусть точка О — точка принадлежащая этому телу (рис. 5.3). Радиус-вектор движущейся точки М относительно точки О можно задать как вектор-функцию времени t

. (1.6).

Равенство (1.6) называется векторным уравнением движения точки или законом движения точки в векторной форме.

Кривая по которой движется точка в пространстве называется траекторией точки. Траектория — это годограф радиус-вектора точки.

Координатный способ задания движения точки

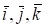
Пусть теперь вектор задан в декартовой системе координат, а — орты осей Ох, Оу, Оz. Тогда вектор-функция может быть задана тремя скалярными функциями :

=++.

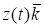
Таким образом, для того, чтобы движение точки было задано координатным способом, должны быть заданы функции:

x = x (t), y= y (t), z = z (t). (1.7).

Равенства (5.7) называются уравнениями движения точки или законом движения точки в координатной форме.

Естественный способ задания движения точки

Этот способ применяется в случае, когда траектория точки известна заранее. Траектория точки может быть задана различными способами: словесно (например, можно сказать, что траекторией точки является окружность такого-то радиуса), графически в каком-либо масштабе или уравнениями, например, в общем виде как линия пересечения поверхностей.

.

или другими уравнениями.

Для задания закона движения точки по траектории необходимо выбрать на траектории точку М₀, принимаемую за начало отсчета дуговой координаты и задать положительное направление отсчета (рис. 1.4.).

При движении точки М расстояние от нее до начальной точки изменяется с течением времени, следовательно, дуговую координату необходимо задать как функцию времени:

s = s (t), (1.8).

Зависимость (1.8) называется законом движения точки. Следовательно, для того, чтобы движение точки было задано естественным способом, должны быть заданы:

• 1) траектория точки;
• 2) закон движения точки s = s (t),
• 3) начало отсчета М₀;
• 4) положительное направление отсчета дуги s.

При этом нужно отличать дугу s и пройденный точкой путь. Если точка движется по траектории все время в одном направлении, то дуга и путь совпадают, но если, например закон движения точки равен и точка совершает гармонические колебания по кривой, то дуга и путь совпадают только до достижения дуги своего максимального значения а. Далее путь в отличие от дуги будет все время увеличиваться.

Скорость и ускорение точки

Скорость точки

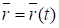
Пусть движение точки задано векторным способом. На рис. 1.5 М и М₁ положения движущейся точки в моменты времени t и t + t.

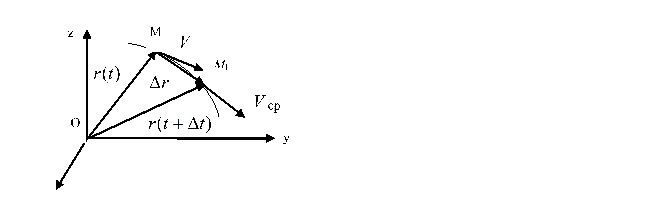
Рис. 1.5.

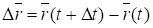
Вектор называется вектором перемещения точки за время t. Отношение вектора к промежут ку времени t называется средней скоростью точки за промежуток времени t

.

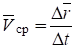
Скоростью точки в данный момент времени называется предел отношения вектора перемещения точки к промежутку времени за который произошло это перемещение, при стремлении последнего к нулю, т. е.

Таким образом, скорость точки в данный момент времени равна производной радиусавектора точки по времени

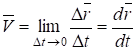
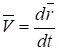
Это векторная величина, характеризующая быстроту изменения радиусавектора точки и направленная по касательной к траектории в сторону движения точки. Единицей измерения скорости в системе СИ является м/с.

Ускорение точки

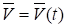
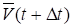
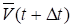
Пусть теперь известна функция. На рис. 5.10 и векторы скорости движущейся точки в моменты t и t. Чтобы получить приращение вектора скорости перенесем параллельно вектор в точку М:

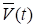
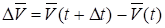
Средним ускорением точки за промежуток времени t называется отношение приращения вектора скорости к промежутку времени t:

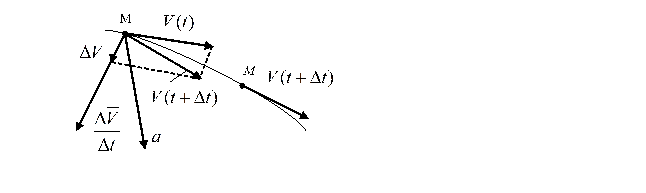
Рис. 1.6.

.

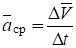
Ускорением точки в данный момент времени называется предел отношения приращения скорости к приращению времени t при стремлении последнего к нулю, т. е.

Следовательно, ускорение точки в данный момент времени равно первой производной по времени от вектора скорости точки или второй производной радиус-вектора по времени

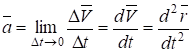
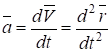
Ускорение точки это векторная величина, характеризующая быстроту изменения вектора скорости по времени.

Построим годограф скорости (рис. 1.7). Годографом скорости по определению является кривая, которую вычерчивает конец вектора скорости при движении точки, если вектор скорости откладывается из одной и той же точки.

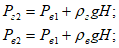
Рис. 1.7.

Очевидно, что скорость точки, вычерчивающей годограф скорости, будет равна ускорению точки при ее движении по траектории.

Единицей измерения ускорения в системе Си является м/с².

Определение скорости точки при координатном способе задания её движения

Пусть движение точки задано координатным способом в декартовой системе координат.

х = x (t), y = y (t), z = z (t).

Радиусвектор точки равен.

.

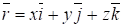
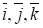
Так как единичные векторы постоянны, то по определению.

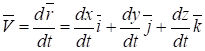
Обозначим проекции вектора скорости на оси Ох, Оу и Oz через V_x, V_y, V_z соответственно и разложим вектор скорости по осям:

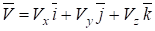
Сравнивая равенства, получим.

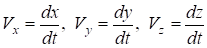
В дальнейшем производную по времени будем обозначать точкой сверху, т. е.

.

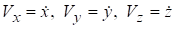
Модуль скорости точки определяется формулой.

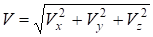
Направление вектора скорости определяется направляющими косинусами:

Определение ускорения точки при координатном способе задания её движения

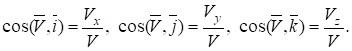
Вектор скорости в декартовой системе координат равен.

.

По определению.

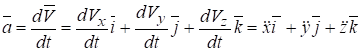
Обозначим проекции вектора ускорения на оси Ох, Оу и Oz через а_x, а_y, а_z соответственно и разложим вектор скорости по осям:

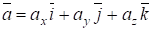
Сравнивая равенства (5.16) и (5.17) получим.

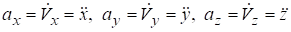
Модуль вектора ускорения точки вычисляется аналогично модулю вектора скорости точки:

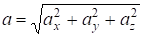
а направление вектора ускорения направляющими косинусами:

Определение скорости и ускорения точки при естественном способе задания её движения

Рис. 1.8.

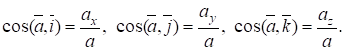
При этом способе используются естественные оси с началом в текущем положении точки М на траектории (рис. 5.12) и единичными векторами Единичный вектор направлен по касательной к траектории в сторону положительного отсчета дуги, единичный вектор направлен по главной нормали траектории в сторону ее вогнутости, единичный вектор направлен по бинормали к траектории в точке М.

Орты и лежат в соприкасающейся плоскости, орты и в нормальной плоскости, орты и в спрямляющей плоскости.

Полученный трехгранник называется естественным.

Пусть задан закон движения точки s = s (t).

Радиус вектор точки М относительно какойлибо фиксированной точки будет сложной функцией времени .

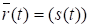
Из дифференциальной геометрии известны формулы СерреФрене, устанавливающие связи между единичными векторами естественных осей и векторфункцией кривой.

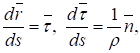
где радиус кривизны траектории.

Используя определение скорости и формулы СерреФрене, получим:

Обозначая проекцию скорости на касательную и учитывая, что вектор скорости направлен по касательной, имеем.

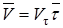
Сравнивая равенств, получим формулы для определения вектора скорости по величине и направлению.

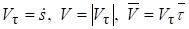
Величина положительна, если точка М движется в положительном направлении отсчета дуги s и отрицательна в противоположном случае.

Используя определение ускорения и формулы СерреФрене, получим:

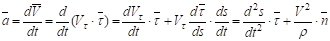
Обозначим проекцию ускорения точки на касательную, главную нормаль и бинормаль соответственно.

Тогда ускорение равно.

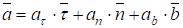
Из формул следует, что вектор ускорения всегда лежит в соприкасающейся плоскости и раскладывается по направлениям и :

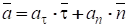
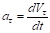
Проекция ускорения на касательную называется касательным или тангенциальным ускорением. Оно характеризует изменение величины скорости.

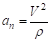
Проекция ускорения на главную нормаль называется нормальным ускорением. Оно характеризует изменение вектора скорости по направлению.

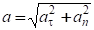
Модуль вектора ускорения равен .

Если и одного знака, то движение точки будет ускоренным.

Если и разных знаков, то движение точки будет замедленным.

Частные случаи движения точки

1. Равномерное криволинейное движение

Пусть .

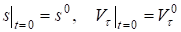
Тогда из следует.

.

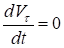
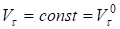
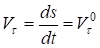
Учитывая, что и, разделяя переменные и интегрируя, получим.

.

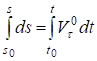
Откуда.

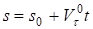
Таким образом, если движение точки равномерное, то дуговая координата изменяется по линейному закону.

2. Равномерное прямолинейное движение.

Так как, то движение точки является прямолинейным, а так как, то оно является и равномерным. Это единственное движение, при котором полное ускорение равно нулю .

3. Равнопеременное движение

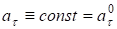
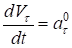
Следовательно, .

Разделяя переменные и интегрируя, получим.

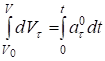
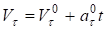
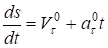
или .

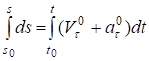
Снова разделяя переменные и интегрируя получим закон равнопеременного движения точки:

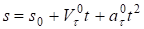
При этом, если (т.е. и одного знака), то движение будет равноускоренным. Если (т.е. и разного знака), то движение будет равнозамедленным.

Отличие от дуги будет все время увеличиваться.