Лекция 4. Сложное движение точки

Рассмотрим движение точки М относительно двух систем координат Oxyz и O₁x₁y₁z₁, движущихся друг относительно друга (рис. 8.1). В механике системы координат предполагаются жестко скрепленными с телами, по отношению к которым рассматривается движение точки. Тела на рисунках можно не показывать.

Рис. 1.1.

Пусть задано движение системы координат Oxyz относительно системы координат O₁x₁y₁z₁. Движение точки М относительно системы координат O₁x₁y₁z₁ называют сложным, если задано ее движение относительно системы координат Oxyz. Систему координат O₁x₁y₁z₁ принимают при этом за неподвижную или основную, а систему координат Oxyz — за подвижную.

Относительное движение

Движение точки М относительно подвижной системы координат называют относительным. Соответственно, траектория (рис. 8.1), скорость и ускорение точки в ее движении относительно подвижной системы координат называются относительными. Относительная скорость и относительное ускорение точки обозначается индексом r:,. Положение точки М по отношению к системе координат Oxyz определяет радиус-вектор .

Введем орты подвижной системы координат и разложим радиус-вектор по ортам.

.

Уравнения.

,.

являются уравнениями относительного движения точки в координатной форме.

Движение самой координатной системы Oxyz не учитывается, считаем ее неподвижной.

Если в уравнениях (8.1) исключить время, то получим уравнения траектории относительного движения (рис. 8.1).

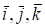
Если относительное движение задано, то для того, чтобы найти относительную скорость точки, необходимо продифференцировать вектор-функцию в предположении, что орты неподвижны.

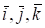
Знак ~ (тильда) в равенстве (8.1а) означает, что производная берется в предположении, что — постоянные векторы. Такая производная называется локальной или относительной производной.

Раскладывая вектор по ортам.

и сравнивая две записи вектора, имеем.

, .

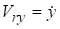
Аналогично ускорение относительного движения точки равно:

Раскладывая вектор по ортам и сравнивая обе записи вектора, имеем.

, .

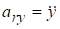
Следовательно, для определения относительной скорости и относительного ускорения точки следует мысленно остановить движение подвижной системы координат и вычислить их по правилам кинематики точки.

Абсолютное движение точки

Движение точки М относительно неподвижной системы координат называют абсолютным. Соответственно, траекторию (рис. 1.1), скорость и ускорение относительно неподвижной системы координат называют абсолютными.

Абсолютная скорость и абсолютное ускорение точки обозначается индексом а:,. Положение точки М относительно неподвижной системы координат O₁x₁y₁z₁ определяется радиус-вектором. Введем орты неподвижной системы координат и разложим по ним радиус-вектор :

.

Тогда уравнения абсолютного движения точки имеют вид.

,.

Исключив в уравнениях время, получим уравнения траектории абсолютного движения точки (рис. 1.1).

Чтобы найти скорость абсолютного движения точки, необходимо продифференцировать вектор-функцию :

.

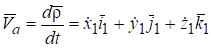
Раскладывая вектор по ортам и, сравнивая обе записи вектора, получим.

, .

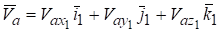
Аналогично, ускорение абсолютного движения точки равно:

.

Раскладывая вектор по ортам.

и сравнивая обе записи вектора, получим.

, .

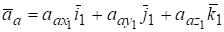
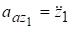
Переносное движение.

Переносным движением точки называется ее движение в рассматриваемый момент времени вместе с подвижной системой координат относительно неподвижной системы координат.

Переносная скорость и переносное ускорение точки обозначается индексом е:, .

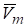
Переносной скоростью (ускорением ) точки М в данный момент времени называют вектор, равный скорости (ускорению ) той точки m подвижной системы координат, с которой совпадает в данный момент движущая точка М (рис. 8.1).

Проведем радиус-вектор начала координат (рис. 8.1). Из рисунка видно, что.

Чтобы найти переносную скорость точки в заданный момент времени необходимо продифференцировать радиус-вектор при условии, что координаты точки x, y, z не изменяются в данный момент времени:

Переносное ускорение соответственно равно.

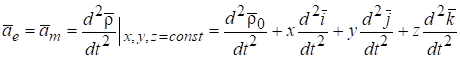
Таким образом для определения переносной скорости и переносного ускорения в данный момент времени необходимо мысленно остановить в этот момент времени относительное движение точки, определить точку m тела, неизменно связанного с подвижной системой координат, где находится в остановленный момент точка М, и вычислить скорость и ускорение точки m тела, совершающего переносное движение относительно неподвижной системы координат.

Постановка задач на сложное движение точки

1. Прямая задача:

По заданным переносному и относительному движениям точки найти кинематические характеристики абсолютного движения точки.

2. Обратная задача:

Некоторое заданное движение точки представить сложным, разложив его на относительное и переносное, и определить кинематические характеристики этих движений. Для однозначного решения этой задачи необходимы дополнительные условия.

Теорема сложения скоростей

Абсолютная скорость точки определяется по теореме о сложении скоростей, согласно которой абсолютная скорость точки, совершающей сложное движение, равна геометрической сумме переносной и относительной скоростей:

Доказательство:

Для определения абсолютной скорости точки продифференцируем выражение справа (8.4) по времени, используя свойства производной вектора по скалярному аргументу:

В последнем выражении слева первые четыре слагаемых по формуле (8.5) представляют переносную скорость, последние три слагаемых по формуле (8.1) — относительную скорость. Теорема доказана.

Теорема сложения ускорений при переносном поступательном движении

Абсолютное ускорение точки, совершающей сложное движение при переносном поступательном движении равно геометрической сумме относительного и переносного ускорения:

Доказательство:

Вернемся к рис. 1.1 При переносном поступательном движении орты не меняются не только по величине, но и по направлению, т. е. это постоянные векторы, а т.к. производные от постоянных векторов, а т.к. производные от постоянных векторов равны нулю, то по формуле.

Для определения абсолютного ускорения точки продифференцируем дважды радиус-вектор (8.4) по времени, учитывая постоянство ортов :

В последнем выражении первое слагаемое по формуле (8.10) представляет переносное ускорение, а последние три по формуле (8.2) — относительное ускорение. Теорема доказана.

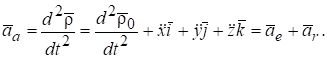
Теорема сложения ускорений при произвольном переносном движении (теорема Кориолиса).

Абсолютное ускорение точки определяется по теореме Кориолиса, согласно которой абсолютное ускорение точки, совершающей сложное движение, равно геометрической сумме переносного, относительно и кориолисова ускорений:

Кориолисово ускорение вычисляется по формуле:

где — вектор угловой скорости переносного движения, — вектор относительной скорости точки.

Направление вектора кориолисова ускорения определяется по правилу векторного произведения: кориолисово ускорение будет направлено перпендикулярно плоскости, в которой лежат векторы и (рис. 8.2), в ту сторону, откуда кратчайший поворот от вектора к вектору видится происходящим против хода часовой стрелки.

Модуль кориолисова ускорения равен .

Рис. 1.2.

Докажем справедливость теоремы для переносного вращательного движения.

Рис. 1.3.

Пусть подвижная система координат Oxyz вращается вокруг оси l с угловой скоростью (рис. 1.3). Во все время движения радиус-векторы точки по-прежнему связаны зависимостью.

.

Так как по определению, продифференцируем выражение по времени, учитывая свойства производной вектора по скалярному аргументу:

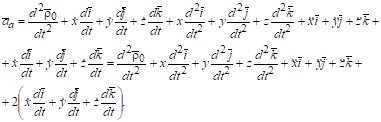
В последнем выражении первые четыре слагаемые представляют переносное ускорение, следующие три слагаемые представляют относительную скорость. Оставшиеся слагаемые обозначим (*). В выражении (*) производная от каждого орта по времени представляет собой линейную скорость точки, для которой этот орт является радиусом-вектором. Например для орта (рис. 8.3) скорость точки А его конца равна.

.

Но так как орт вращается вокруг оси l, то скорость его конца можно определить по векторной формуле Эйлера:

.

Следовательно Аналогично для ортов и :

.

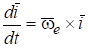
Подставляя формулы (8.14) и (8.15) в выражение (*), получим.

(*) =.

Используя сочетательное свойство векторного произведения относительно числовых множителей, какими являются, имеем.

(*) =.

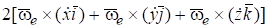
Далее, используя распределительное свойство для векторного произведения, получим.

(*) =.

Таким образом,.

.

Теорема для переносного вращательного движения доказана.