Политропный (политропический) процесс

Уравнение политропы. Определение показателя политропы

Из физики известно четыре простейших процесса (изопроцесса):

• 1) изобарный;
• 2) изохорный;
• 3) адиабатный;
• 4) изотермический,

Для сравнения изобразим на рис. 10 эти процессы, проходящими через общую точку А:

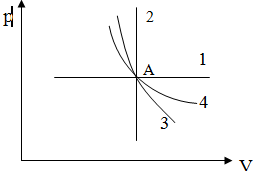
рис. 10. Изопроцессы в P-V координатах.

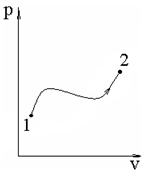
рис. 11. Пример политропного процесса.

Но в целом ряде случаев реальные процессы, например рис. 11, не соответствуют ни одному из изопроцессов.

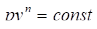
Для выполнения теплотехнических расчётов в таких случаях, пусть даже с какими-то погрешностями, реальный процесс заменяется гипотетическим, имеющим формулу, удобную с точки зрения математических преобразований. Этому требованию удовлетворяет уравнение вида. Так как это уравнение должно описывать всё многообразие реальных процессов, то в этом уравнении должен присутствовать коэффициент согласования (идентификации). Этим коэффициентом является показатель степени n, называемый показателем политропы. Так как n коэффициент согласования, то, в отличие от показателя адиабаты k в уравнении Пуассона, где k>1, показатель политропы может иметь любые значения в интервале (,+). Показатель политропы определяется только путем обработки опытных данных.

Алгоритм определения показателя политропы n.

• 1) Разбиваем pv-диаграмму реального процесса на N точек (чем больше точек, тем точнее n).
• 2) Снимаем с pv-диаграммы реального процесса значение давления p_i удельного объёма v_i в каждой i-той точке и заносим в таблицу.
• 3) Для каждой i-той точки вычисляем значения lnp_i и lnv_i и заносим в таблицу.
• 4) Перестраиваем pv-диаграмму в координатах: lnp — lnv.
• 5) Аппроксимируем точки на графике в логарифмических координатах одной прямой, используя метод наименьших квадратов или другой аналогичный метод. Если это удаётся без значительных погрешностей, то тангенс угла наклона прямой к оси lnv равен показателю политропы.

На рис. 12 и 13 представлен пример определения показателя политропы.

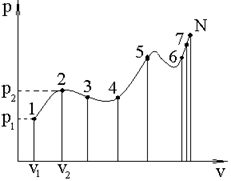
Рис. 12. Пример обработки опытных данных для определения показателя политропы

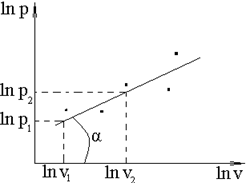
Рис. 13. Пример определения показателя политропы.

Таблица 7.

Если все точки не укладываются удовлетворительно на одной прямой, то используется метод линейно-кусочной аппроксимации, по которому показатели политропы определяются для отдельных участков процесса.

В этом случае реальный процесс рассчитывается по уравнению pvⁿ = const при последовательно изменяющемся значении показателя политропы n: n₁, n₂, n₃ и т. д. Значения А, Q, U, найденные на отдельных участках процессов затем суммируются.

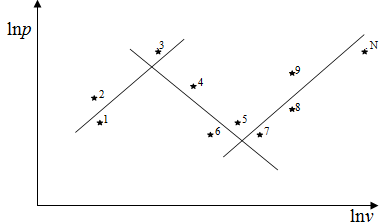
Рис. 14. Пример определения показателей политропы для отдельных участков

В тех случаях, когда расчёты выполняются для небольшого участка процесса или для всего процесса известны только две точки, можно использовать метод определения показателя политропы n по двум точкам.

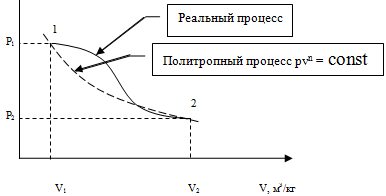
Рис. 15. Иллюстрация к методу определения n по двум точкам

Если реальный процесс задан pv-координатах, то используется уравнение политропы в виде.

pvⁿ = p₁v₁ⁿ = p₂v₂ⁿ =const.

После логарифмирования и приведения подобных, получим искомое значение n:

ln p1 + n ln v1 = ln p2 + n ln v2

ln p₁ — ln p₂ = n (ln v₂ — ln v₁).

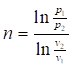
(139).

В политропном процессе газ считается идеальным. Так как основное уравнение политропы pvⁿ =const по форме совпадает с уравнением адиабаты идеального газа pv^k =const (уравнение Пуассона), то без вывода запишем еще два уравнения политропы:

(140).

(141).

Для определения показателя политропы может использоваться любое из трех уравнений политропы.

Так как теплоёмкость является функцией процесса, то получим формулу для теплоёмкости в политропном процессе с_n:

Из общей формулы теплоёмкостей однородных систем (74) для политропного процесса имеем:

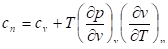
(формула (76)).

Так как в политропном процессе газ считается идеальным, то.

(формула (77)).

Требуется найти. Для этого воспользуемся уравнением политропы (140):

.

Логарифмируя и дифференцируя это уравнение, приводя подобные получим:

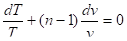
Откуда.

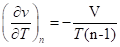
Подставим найденное значение в уравнение (76):

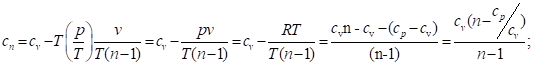
Окончательно.

(142).

В (142) показатель адиабаты k>1, в то время как n (, +).

При 1_n получается отрицательным. С физической точки зрения это трудно объяснимо, поэтому, придавая отрицательной величине c_n формальный характер, вычисление А, Q, U проводим с этим отрицательным значением.

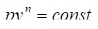
Изопроцессы, в силу универсальности уравнения, можно рассмотривать как частные случаи политропного процесса:

• 1) при n = 0 получается уравнение изобарного процесса (p=const);
• 2) при n = 1 — уравнение изотермического процесса (pv=const);
• 3) при n = k — уравнение адиабатного процесса pv^k=const (или S=const);
• 4) при n = - уравнение изохорного процесса (v=const).

На рис. 16 представлены различные процессы с указанием значений показателя политропы. Пунктирной линией в качестве примера изображены процессы, не относящиеся к изопроцессам.

рис. 16. Показатель политропы для различных процессов.

IV.2 Работа, теплота и внутренняя энергия в политропном процессе Как известно, удельная абсолютная деформационная работа определяется по формуле:

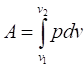
Для того, чтобы найти этот интеграл, необходимо знать уравнение, связывающее давление и объем. Таким уравнением является уравнение политропы pvⁿ=const. Запишем это уравнение развернутом виде:

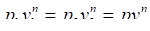
откуда Тогда Окончательно.

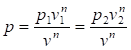
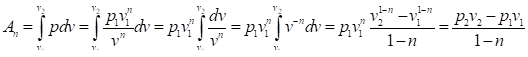
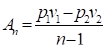
(143).

Так как в политропном процессе газ считается идеальным, то преобразуем (143) к виду:

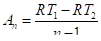
Или окончательно:

(144).

Получим ещё несколько формул для А_n, для чего подставим в (144), найденные из других уравнений политропы. Из уравнения.

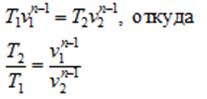
(144*) Тогда.

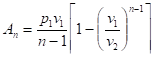
(145).

Из уравнения следует.

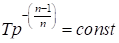
(146).

После подстановки (146) в (144) окончательно получим.

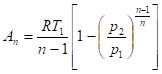
(147).

Формула (147) широко используется в теории газовых турбин, газовой динамике и так далее.

Внутренняя энергия идеального газа зависит только температуры, поэтому соотношение (73) для идеального газа примет вид.

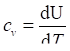
(148).

откуда после интегрирования при с_v=const.

(149).

Формула (148) справедлива для любого процесса, в том числе и для политропного, поэтому.

(150).

Как известно.

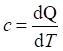
откуда для политропного процесса.

dQ_n=c_ndT (151).

После подстановки (142) в (151) и интегрирования при окончательно получим:

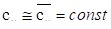
(152).

IV.3 Изменение энтропии в политропном процессе Для обратимых процессов, как известно.

dQ = T dS

Так как одновременно.

dQ = c dT,.

то из равенства правых частей этих уравнений получим.

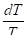
dS = c (153).

Из (153) и (142) для политропного процесса.

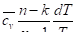
dS_n = ,.

Откуда после интегрирования окончательно получим:

(154).

Подставляя в (154) отношения из (144*) и (146) получим еще две формулы для расчета? S_n:

(155).

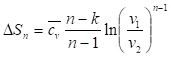
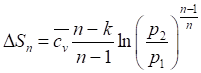
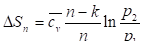
(156).

Как известно, в инженерных расчетах полагают, что энтропия равна нулю при нормальных физических условиях. Тогда, подставляя в (154) Т_н вместо Т₁ и Т вместо Т₂ получим формулу для расчета энтропии:

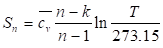
(157).

Из формул (155) и (156) аналогично получим:

(158).

(159).