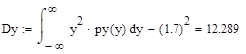Основы стохастического анализа

Задание 1

Постройте:

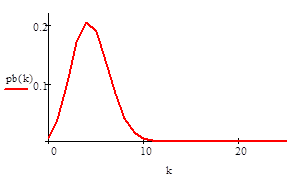
• 1) биномиальное распределение для серии из п независимых испытаний с вероятностью успеха р,
• 2) пуассоновское распределение с параметром ,
• 3) гипергеометрическое распределение с параметрами N, М, п,
• 4) геометрическое распределение с параметрами п, р.
• 5) распределение Паскаля с параметрами п, р., r

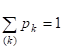
Для каждого распределения выполните следующее: проверьте равенство, где p_k = P (Х = k); найти значение k, для которого величина Р (X = k) максимальна; постройте графики распределения и функций распределения; Найти вероятность попадания значений случайной величины в интервал (а, b).

Таблица. Биномиальное распределение.

Решение:

,.

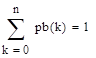
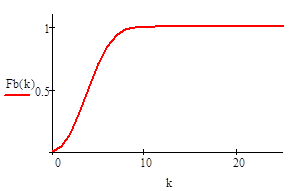
Пуассоновское распределение.

.

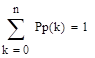
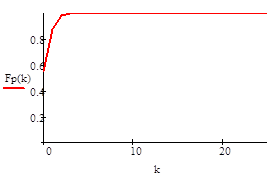
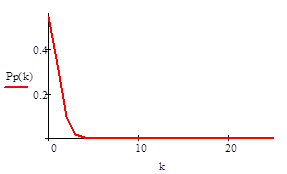
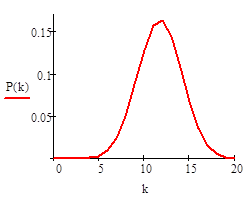
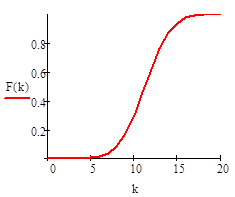
Геометрическое распределение.

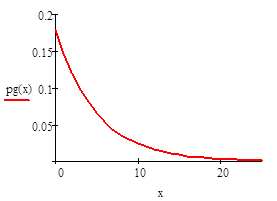
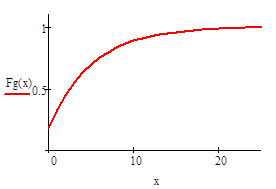
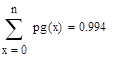
Распределение Паскаля.

.

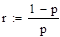
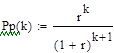
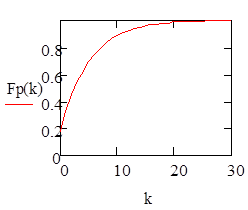
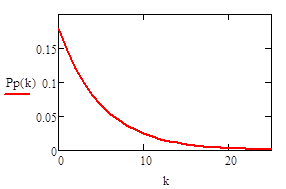
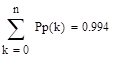
Мы здесь получили для распределения Паскаля те же результаты что и для геометрического распределения. Это объясняется тем, что из распределения Паскаля можно получить геометрическое:

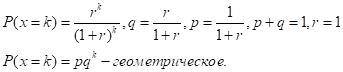
При произвольном p распределение Паскаля имеет следующий вид:

Задание 2

Исследуйте для приведенного в задании эксперимента точность асимптотической формулы Пуассона. Вычислите вероятность события X > k для биномиального распределения и по приближенной формуле Пуассона = пр. Для сравнения выполните вычисления для n₁= 0.0l n и p₁ = 100р.

Варианты 1−10. Провайдер обслуживает п абонентов сети Internet. Вероятность того, что любой абонент захочет войти в сеть в течение часа, равна р. Найти вероятность того, что в течение часа более k абонентов попытаются войти в сеть.

— биномиальное распределение.

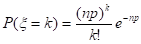
— распределение Пуассона.

Решение:

.

Из приведенных вычислений видно, что в первом случае (n = 1800, p = 0.0022) результаты вычислений по точной и асимптотической формулам совпадают, а во втором (n = 18, p = 0.22) — отличаются.

Задание 3

Исследуйте для указанных значений параметров биномиального распределения точность асимптотической формулы Муавра — Лапласа.

Исследуйте для указанных значений параметров биномиального распределения точность локальной формулы Муавра — Лапласа. Для указанных значении п и р вычислите вероятность того, что случайная величина, имеющая биномиальное распределение, принимает значение, равное п/2 Проведите вычисления по формуле Бернулли и по приближенной формуле Муавра — Лапласа. Сравните результаты.

На практике пуассоновским приближением пользуются при npq < 9. Если npq > 9, то для расчетов используют приближение в соответствии с теоремой Муавра — Лапласа. Пусть и величина:

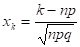
ограничена при, тогда:

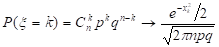
Требование ограниченности величины x_k означает, что при величина k тоже должна расти вместе с величиной n. Точность формулы:

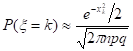
растет как с ростом величин n и k, так и по мере приближения величин p и q к .

Решение:

.

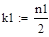
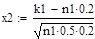
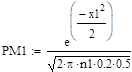
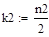
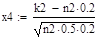
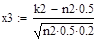
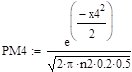
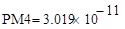
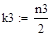
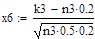
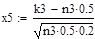
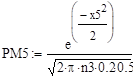
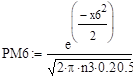
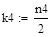
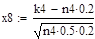
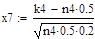
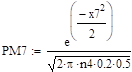
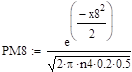
Приведенные вычисления полностью подтверждают теоретические утверждения: погрешность аппроксимации уменьшается с ростом п и по мере приближения p и q к 0.5.

Задание 4

Исследуйте для указанного биномиального распределения точность интегральной формулы Муавра — Лапласа.

Варианты 1−10. Вероятность того, что произвольно выбранный абонент сети Internet — студент, равна р. Найти вероятность того, что среди абонентов некоторого провайдера студентов не менее k₁ и не более k₂.

Для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k₁ и k₂, можно использовать формулу:

.

.

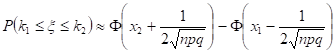
Решение:

.

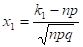
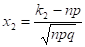
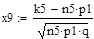
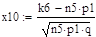
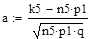
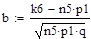
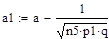
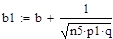
Приведенные вычисления полностью подтверждают теоретические утверждения: приближенные значения вероятностей совпадают с вероятностями, вычисленными по формуле Бернулли.

Задание 5

Найдите наименьшее число испытаний Бернулли, необходимое для того, чтобы с вероятностью, не меньшей заданной, можно принять относительную частоту успехов за вероятность успеха в одном испытании с погрешностью, не превышающей заданную.

Варианты 1−10. Провайдер утверждает, что вероятность соединиться с сетью с первого звонка достаточно велика. Сколько нужно произвести экспериментов, чтобы с вероятностью не менее можно было утверждать, что относительная частота соединений с первого звонка отличается от заявленной вероятности не более, чем на ?

Определим, сколько нужно произвести испытаний, чтобы отклонение относительной частоты успехов от вероятности p было меньше e с вероятностью, большей или равной, т. е. найдем n, для которого выполняется неравенство:

.

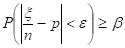
Доказано, что число n обеспечивает выполнение этого неравенства, если оно удовлетворяет соотношению:

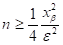
где x — решение уравнения:

.

Следует обратить особое внимание на замечательный факт — искомое значение n не зависит от p и поэтому формулой:

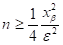
следует пользоваться для оценки минимально необходимого числа испытаний при неизвестной вероятности р. Если вероятность p изначально известна, то необходимое число испытаний определяется формулой:

.

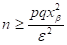
Решение:

.

.

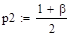
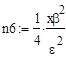
Искомое значение n= 157.

Задание 6

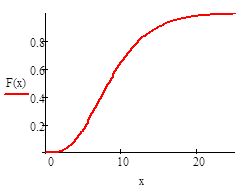
Постройте графики плотности распределения и функции распределения ² c указанным числом степеней свободы, равным п = 9.

Распределение xи-квадрат (²-распределение). Пусть x₁, x₂, … x_n — независимые случайные величины, каждая из которых имеет стандартное нормальное распределение N(0, 1). Составим случайную величину:

.

Ее распределение называется ²-распределением с n степенями свободы. Для справочных целей приведем здесь выражение плотности распределения этой случайной величины:

.

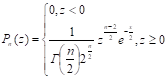
где Г(x) — гамма-функция Эйлера:

.

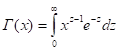
Решение:

.

Задание 7.

Постройте графики плотности распределения и функции распределения Стьюдента с указанным числом степеней свободы, равным k = №. Здесь № - номер варианта.

Распределение Стьюдента. Пусть случайная величина x имеет стандартное нормальное распределение, а случайная величина ²-распределение с n степенями свободы. Если x и независимы, то про случайную величину:

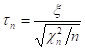
говорят, что она имеет распределение Стьюдента с числом степеней свободы п. Доказано, что плотность вероятности этой случайной величины вычисляется по:

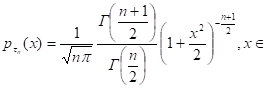
R.

При больших n распределение Стьюдента практически не отличается от N(0,1).

Решение:

N.	п.	т.

Задание 8

Постройте графики плотности распределения и функции распределения Фишера для указанных значений n и m.

F-распределение Фишера. Пусть случайные величины и независимы и имеют распределение ² с n и m степенями свободы соответственно. Тогда случайная величина:

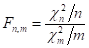
имеет F-распределение с плотностью вероятности:

x > 0.

Решение:

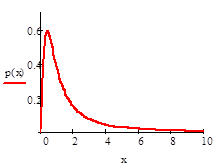
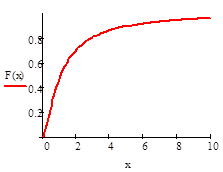
Задание 9.

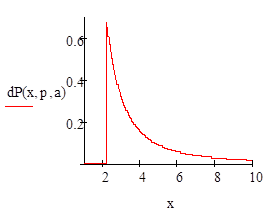
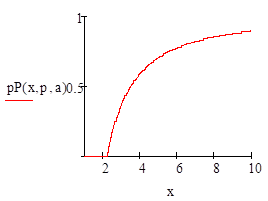
Постройте графики плотности распределения и функции распределения Парето для указанных значений a и .

Распределение Парето. Распределение Парето часто применяется в экономических исследованиях. Плотность вероятностей для случайной величины, распределенной по Парето, имеет вид:

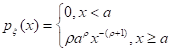
где .

Как видно из этой формулы, случайная величина, распределенная по Парето, принимает значения только в области x > а.

Решение:

.

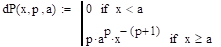
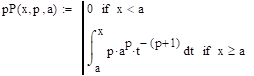
Задание 10.

Постройте графики плотности распределения и функции распределения для логистического распределения при значениях параметров = а и = для значений а и из задания 9.9.

Логистическое распределение. Это еще одно распределение, широко применяемое в экономических исследованиях. Оно имеет следующую функцию распределения:

R.

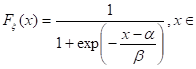
где и — параметры распределения.

Плотность распределения вероятностей для логистического распределения вычисляется по формуле:

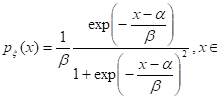
R.

По своим свойствам логистическое распределение очень похоже на нормальное.

Решение:

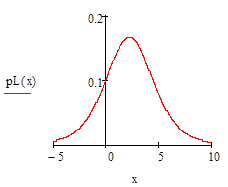
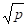
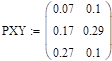
Задание 11.

Найдите медиану, верхнюю и нижнюю квартили, а также 95%-ную квантиль для нормального распределения N(a,), а и = для значений и из задания 9.9.

При решении практических задач часто требуется найти значение я, при котором функция распределения случайной величины принимает заданное значение, т. е. требуется решить уравнение.

F_о (x) = p.

Решения такого уравнения в теории вероятностей называются квантилями.

Квантилъю x_p (p-квантилью, квантилью уровня p) случайной величины о, имеющей функцию распределения F_о(x), называют решение x_p уравнения:

F_о (x) = p, p (0,1).

Для некоторых p уравнение F_о (x) = p может иметь несколько решений, для некоторых — ни одного. Это означает, что для соответствующей случайной величины некоторые квантили определены неоднозначно, а некоторые квантили не существуют.

Квантили, наиболее часто встречающиеся в практических задачах, имеют свои названия:

медиана — квантиль уровня 0.5;

нижняя квартиль — квантиль уровня 0.25;

верхняя квартиль — квантиль уровня 0.75;

децили — квантили уровней 0.1, 0.2, …, 0.9;

процентили — квантили уровней 0.01, 0.02, …, 0.99.

Решение:

квантиль уровня 0.95.

Задание 12

По заданному совместному распределению двух дискретных случайных величин найдите распределение каждой из них.

Решение:

.

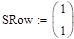
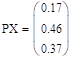
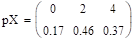
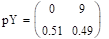
Распределение х:

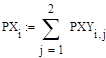
Распределение у.

Задание 13

По заданному совместному распределению двух дискретных случайных величин найдите распределение каждой из них и проверьте их независимость.

Решение:

— распределение х.

— распределение у Проверка независимости:

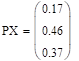
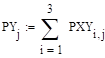
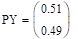
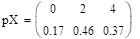
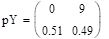
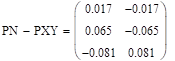
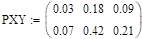
Условие независимости не выполняется, следовательно, X и Y зависимы. распределение случайная вероятность дисперсия.

Для распределений из 13

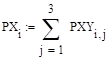
— распределение х.

— распределение у Проверка независимости:

.

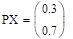
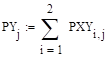
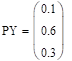
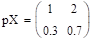
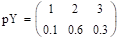
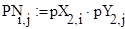
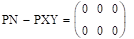
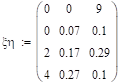
Задание 14

Вычислите распределение компонент заданной двумерной случайной величины и все их условные распределения. Постройте многоугольники соответствующих распределений. Выполните вычисления для распределений из задания 9.12.

Решение:

Распределение СВ.

Распределение СВ.

.

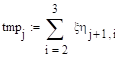
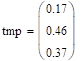
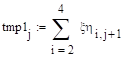
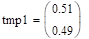
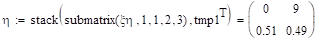
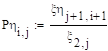
Распределение СВ.

Условные распределения при х=0, 2, 4.

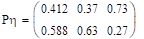
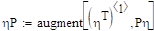
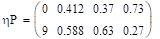
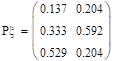
Условные распределения при у=0, 9.

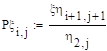
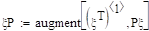
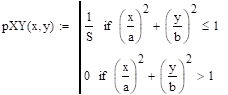
Задание 15.

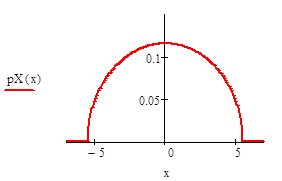
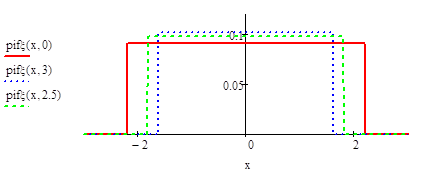
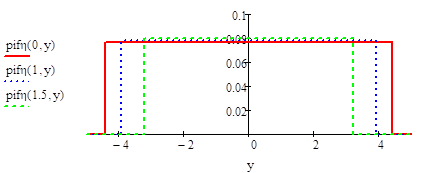
Найти распределение компонент двумерной случайной величины и все их условные распределения, если эта случайная величина распределена равномерно в области х ² /а ²+у ² / b² 1.

Решение:

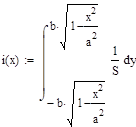
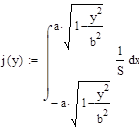
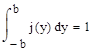
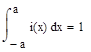
Проверка выполнения условия нормировки:

.

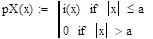
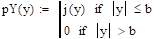
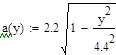
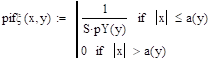
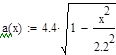
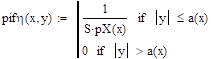
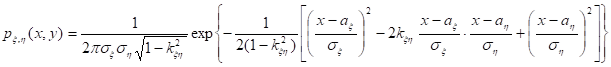
Задание 16.

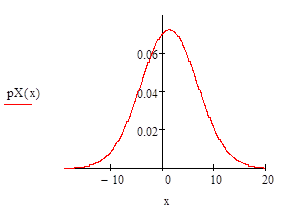
Вычислите плотности вероятностей и условные плотности вероятностей нормального случайного вектора (X, Y) с заданными параметрами. Постройте график плотности вероятностей случайного вектора, графики плотности вероятностей компонент случайного вектора и графики условных плотностей вероятностей каждой компоненты, когда значение другой компоненты равно ее математическому ожиданию.

Важный пример дает случайный вектор (о, з), имеющий нормальное распределение. В наиболее общем случае плотность вероятностей такого вектора зависит от пяти параметров а_о, а_з, у_о, у_з, k_оз и имеет вид:

При любых значениях параметров а_о, а_з, у_о>0, у_з>0, |k_оз|1 эта функция удовлетворяет условиям нормировки:

.

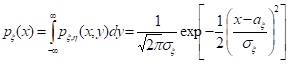
Кроме того, можно легко найти плотность распределения каждой из случайных величин о и з:

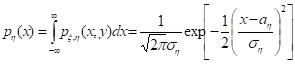
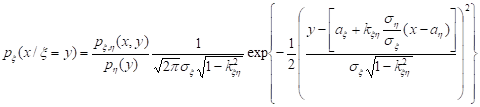
т.е. случайные величины о и з имеют нормальные распределения с параметрами a_о, у_о > 0, и a_з, у_з > 0:

о ~ N(a_о, у_о), з ~ N(a_з, у_з).

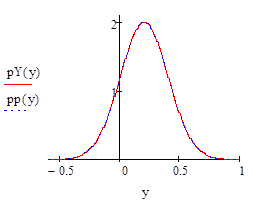
Аналогично можно найти условное распределение.

Рассмотрим теперь условное распределение о при условии з = у. Для этого, выполнив несложные вычисления, найдем:

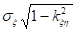
Это нормальное распределение с параметрами:

и .

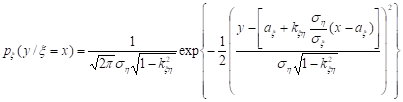
Аналогично можно найти условное распределение:

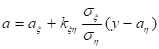
которое также является нормальным распределением с параметрами:

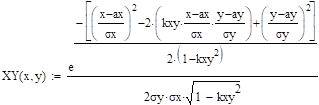
и .

Решение:

.

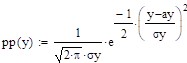
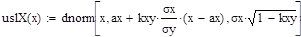
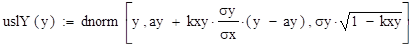
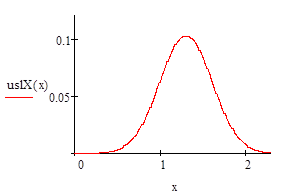
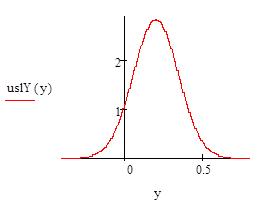
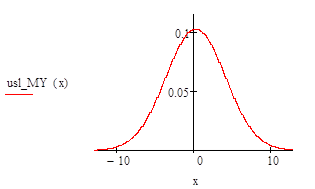
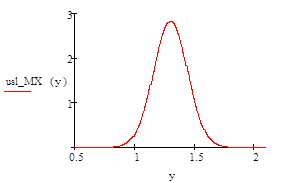
Задание 17.

Найдите по заданному распределению аргумента функцию случайной величины Y=g (X) и ее распределение .

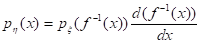
Если о — случайная величина с областью значений Х_о и функция f(x) определена на множестве Х_о, то з = f(x) — тоже случайная величина. Задача об отыс. кании функции распределения случайной величины з по известной функции распределения случайной величины о легко решается, если f(x) — непрерывная монотонно возрастающая функция. В этом случае:

F_з(x) = P(з(f(о)(о^-1(x)) = F_о(f^—1(x)).

F_з(x)=F_о(f^—1(x)).

Здесь F_о(x) — известная функция распределения случайной величины о, а символом f^—1(x) обозначена функция, обратная к функции* f^—1(x).

Плотность распределения случайной величины з для дифференцируемой функции f(x) находится по формуле:

.

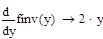
Решение:

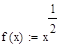
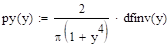
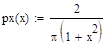
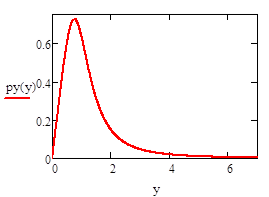
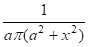
Y — принимает положительные значения, при отрицательных значениях Y распределение равно нулю.

Задание 18

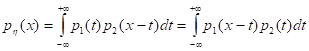
Найдите плотность распределения вероятности суммы двух независимых непрерывных случайных величин, заданных своими плотностями вероятностей р ₁(х) и p₂(х). Здесь Arctg [a] - распределение арктангенса с плотностью .

В теории вероятностей очень часто возникает необходимость в определении плотности вероятности суммы двух независимых случайных величин. Если о₁ и о₂ — непрерывные независимые случайные величины с плотностями вероятности соответственно р ₁(х) и p₂(х), то плотность вероятностей суммы з=о₁+о₂ вычисляется по формуле:

.

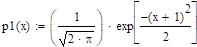
Интеграл такого вида называется сверткой функций р ₁(х) и р ₂(х).

Решение:

.

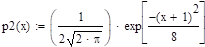
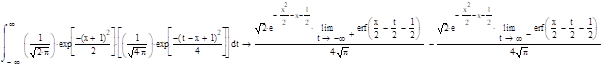
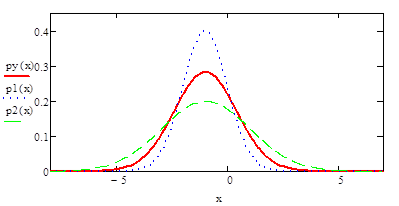
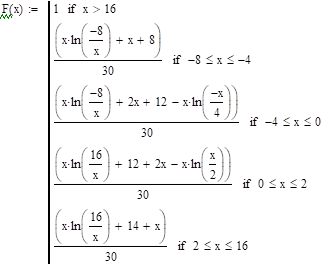
Задание 19.

Найдите функцию распределения произведения двух зависимых случайных величин, распределенных равномерно в соответствии на промежутках [а, b] и [с, d].

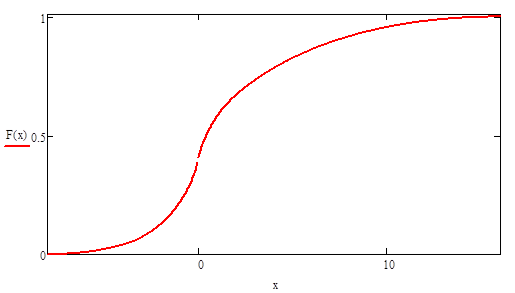
Решение:

— непрерывная случайная величина, где.

.

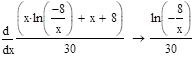
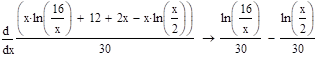
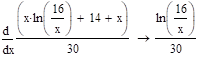
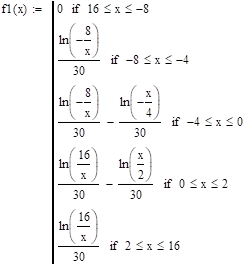
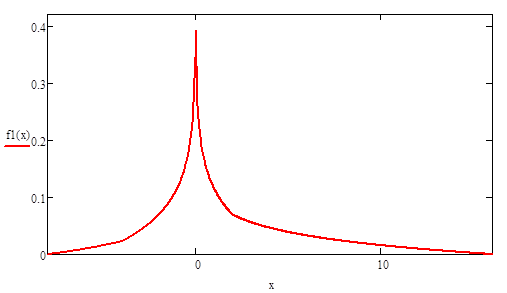
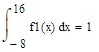
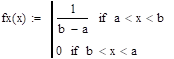
Плотность распределения функции можно найти простым дифференцированием функции распределения случайной величины по .

Задание 20

Вычислите математическое ожидание и дисперсию слyчайной величины Y = (X), которая представляет собой площадь указанной в задании геометрической фигуры, для случайной величины X, распределенной равномерно на промежутке [а, b].

Решение:

.

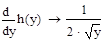
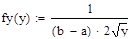
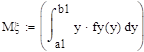
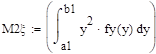
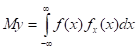
Так как случайная величина y является функцией случайной величины x, y=f(x), то:

.

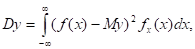
А дисперсия вычисляется по формуле:

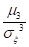
Dy = Мy² — (Мy)².

Задание 21

Вычислите коэффициент асимметрии СВ x (=Х) с заданным распределением.

В теории вероятностей и математической статистике, помимо математического ожидания и дисперсии, используются и другие числовые характеристики случайных величин. В первую очередь это начальные и центральные моменты.

Начальным моментом k-го порядка случайной величины x называется математическое ожидание k-й степени случайной величины x, т. е.

_k = Мx^k.

Центральным моментом k-го порядка случайной величины x называется величина _k, определяемая формулой:

_k = М(x — Mx)^k.

Заметим, что математическое ожидание случайной величины — начальный момент первого порядка,.

₁ = Мx,.

а дисперсия — центральный момент второго порядка:

₂ = М(x — Mx)² = Dx.

Существуют формулы, позволяющие выразить центральные моменты случайной величины через ее начальные моменты. Одна из таких формул приведена выше:

Dx = М(x — Mx)² = ₂ — ₁².

В дальнейшем будет использована формула:

₃ = _3-3₂₁+ 2₁³

Нетрудно понять, что если плотность распределения вероятностей случайной величины симметрична относительно прямой:

х = Мx,.

то все ее центральные моменты нечетного порядка равны нулю.

В теории вероятностей и в математической статистике в качестве меры асимметрии распределения служит коэффициент асимметрии, который определяется формулой:

_x =

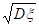
где ₃ — центральный момент третьего порядка;

_x = =.

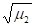
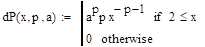
— среднеквадратичное отклонение.

Коэффициент асимметрии — безразмерная величина, а по его знаку можно судить о характере асимметрии.

Решение:

.

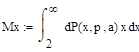
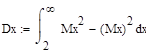
Т.к нельзя вычислить коэффициент асимметрии.

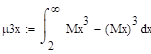
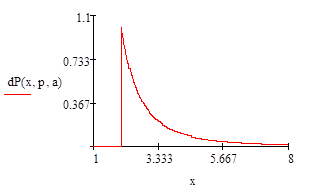
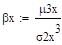
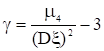
Задание 22.

Вычислите эксцесс случайной величины x с заданным распределением. Выполните вычисления для распределений из задания 2l.

Нормальное распределение наиболее часто используется в теории вероятностей и в математической статистике, и поэтому график плотности вероятностей нормального распределения стал своего рода эталоном, с которым сравнивают другие распределения. Одним из параметров, определяющих отличие сравниваемого распределения от нормального, является эксцесс.

Эксцесс случайной величины x определяется равенством:

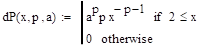
У нормального распределения, естественно, = 0. Если > 0, то это означает, что график плотности вероятностей p_x(х) сильнее «заострен», чем у нормального распределения, если же < 0, то «заостренность» графика p_x(х) меньше, чем у нормального распределения.

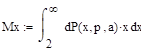
Решение:

.

Задание 23

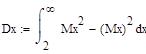
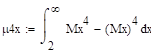
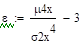
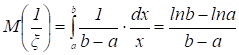
Вычислите среднее геометрическое и среднее гармоническое неотрицательной случайной величины x с заданным распределением.

Средним гармоническим случайной величины, принимающей положительные значения, называется величина.

H_x = M(x ^-1)^-1.

Например, для непрерывной случайной величины, распределенной равномерно на отрезке [а, b], 0 < a < b, среднее гармоническое вычисляется следующим образом:

.

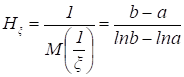
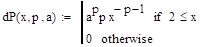
Средним геометрическим случайной величины, принимающей положительные значения, называется величина:

G_x = e^M(lnx).

Решение:

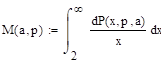
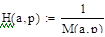
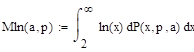
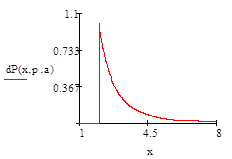
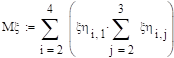
Задание 24.

Вычислите математическое ожидание дискретного двумерного случайного вектора с заданным распределением. Выполните вычисления для распределения из задания 9.12.

Решение:

Распределение двумерной случайной величины.

Математическое ожидание x.

Математическое ожидание h.

.

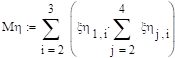
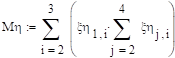
Задание 25

Вычислите дисперсию дискретного двумерного случайного вектора с заданным распределением. Выполните вычисления для распределения из задания 9.12.

Решение:

Распределение двумерной случайной величины

Математическое ожидание x.

Математическое ожидание h.

Математическое ожидание x2.

Математическое ожидание h2.

Дисперсия x.

Дисперсия h.

.

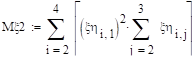
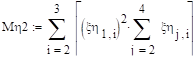
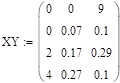
Задание 26.

Вычислите условные математические ожидания и постройте графики регрессий компонентов двумерных случайных величин из заданий 9.14 и 9.15.

х ² /а ²+у ² / b² 1.

Решение:

Из 14.

.

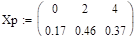
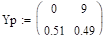
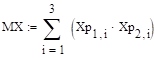
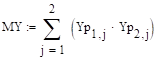
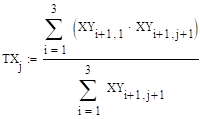
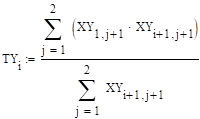
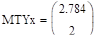
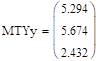
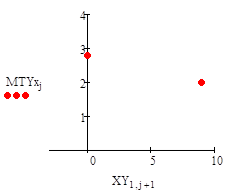
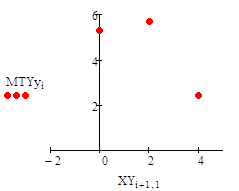
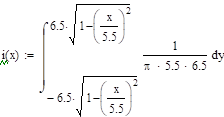
Из 15.

.

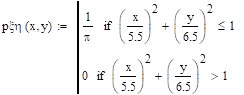
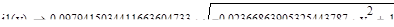
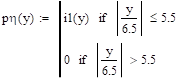
Распределение плотности вероятностей СВ.

.

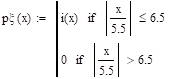
Математическое ожидание:

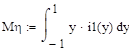
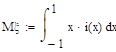
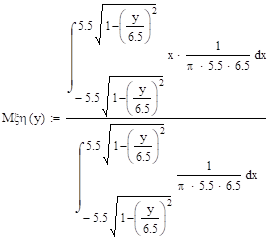
Условные математические ожидания.

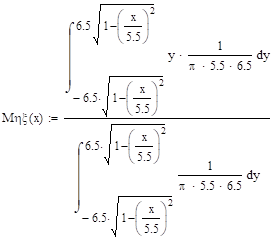
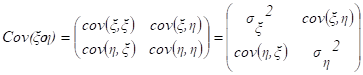
Задание 27.

Вычислите ковариацию и дисперсию компонент двумерных случайных величин из заданий 14 и 15.

х ² /а ²+у ² / b² 1.

Если между случайными величинами x и h существует стохастическая связь, то одним из параметров, характеризующих меру этой связи, является ковариация cov (x, h). Ковариацию вычисляют по формулам:

cov (x, h) = M [(x — Mx)(h — Mh)]= M(xh) — Mx Mh.

Если случайные величины x и h независимы, то cov (x, h) = 0. Обратное, вообще говоря, неверно. Из равенства ковариации нулю не следует независимость случайных величин. Случайные величины могут быть зависимы, в то время как их ковариация нулевая!

Но зато, если ковариация случайных величин отлична от нуля, между ними существует стохастическая связь, мерой которой и является величина ковариации.

Интересно отметить, что.

cov (x, x) = Dx.

cov (h, h) = Dh.

Кроме того, важны следующие свойства ковариации:

cov(x + C₁, h + C₂) = cov(x, h);

cov(x, h) = cov(h, x);

cov(C₁x + C₂h,) = C₁ cov(x,) + C₂ cov(h,).

Ковариационной матрицей случайного вектора (x, h) называется матрица вида:

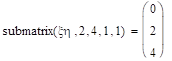
Эта матрица симметрична и положительно определена. Ее определитель называется обобщенной дисперсией и может служить мерой рассеяния системы случайных величин (x, h).

Как уже отмечалось ранее, дисперсия суммы независимых случайных величин равна сумме их дисперсий:

D (x, h) = Dx + Dh.

Если же случайные величины зависимы, то:

D(x h) = Dx + Dh 2cov(x, h).

Решение:

Распределение случайной величины :

Распределение случайной величины :

.

Ковариация:

.

Дисперсия +.

Распределение +.

.

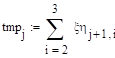
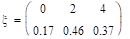
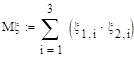
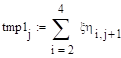
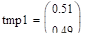
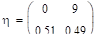
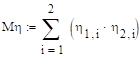
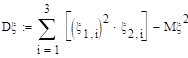
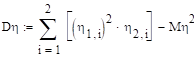
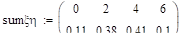
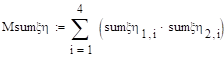
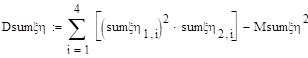
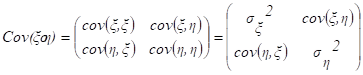
Задание 28

Вычислите ковариационную и корреляционную матрицы двумерного случайного вектора из задания 14.

Ковариационной матрицей случайного вектора (x, h) называется матрица вида:

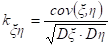
Эта матрица симметрична и положительно определена. Ее определитель называется обобщенной дисперсией и может служить мерой рассеяния системы случайных величин (x, h).

Понятно, что значение ковариации зависит не только от «тесноты» связи случайных величин, но и от самих значений этих величин, например, от единиц измерения этих значений.

Для исключения этой зависимости вместо ковариации используется коэффициент корреляции:

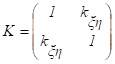
Этот коэффициент обладает следующими свойствами:

• * он безразмерен;
• * его модуль не превосходит единицы, т. е. | k_xh | 1;
• * если x и h независимы, то k_xh = 0 (обратное, вообще говоря, неверно!);
• * если | k_xh | = 1, то случайные величины x и h связаны функциональной зависимостью вида:
• h = ax + b,

где а и b — некоторые числовые коэффициенты;

* k_xx = k_hh = 1.

Корреляционной матрицей случайного вектора называется матрица:

.

.

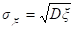
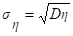
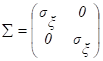
то ковариационная и корреляционная матрицы случайного вектора (x,h) связаны соотношением:

Cov (x,h) = K,.

.

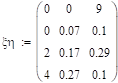
Решение:

Распределение двумерной случайной величины:

Распределение случайной величины:

Математическое ожидание:

Распределение случайной величины:

:

Математическое ожидание:

.

.

.

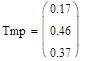
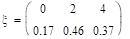
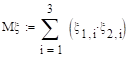
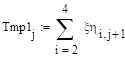
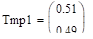
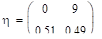
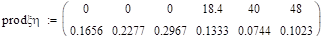
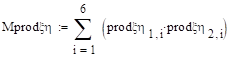
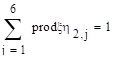
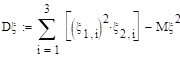
Ковариация:

.

Дисперсия:

.

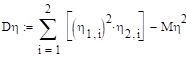
Дисперсия +.

Распределение +.

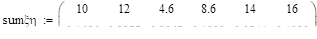
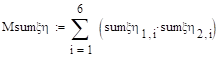
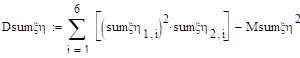
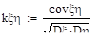
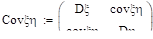
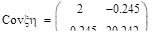
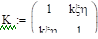
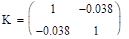
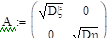
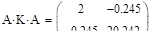
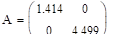
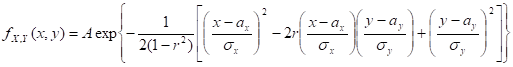
Задание 29.

По заданной плотности вероятностей нормального двумерного распределения:

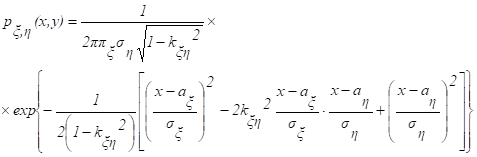
найдите нормировочный множитель А, вычислите ковариационную и корреляционную матрицы.

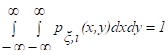
При любых значениях параметров a_x, a_h, _x, _h, k_xh эта функция удовлетворяет условиям нормировки:

.

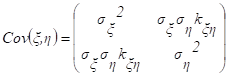
Параметры a_x, a_h, _x, _h, k_xh имеют простой теоретико-вероятностный смысл:

a_x — математическое ожидание случайной величины x,.

Мx = a_x;

a_h — математическое ожидание случайной величины h,.

Мh = a_h;

_x — среднеквадратичное отклонение случайной величины x,.

Dx = _x²;

_h — среднеквадратичное отклонение случайной величины h,.

Dh = _h²;

k_xh — коэффициент корреляции случайных величин x и h.

Таким образом, зная плотность вероятностей двумерного нормального распределения, можно найти его числовые характеристики и построить ковариационную и корреляционную матрицы:

.

Решение:

.

.

.

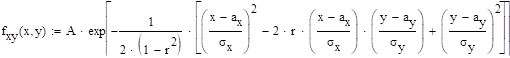
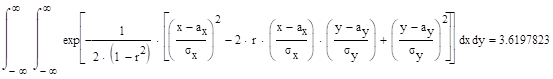
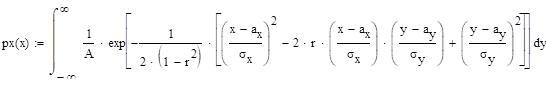
Плотность вероятностей x:

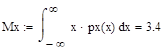
Математическое ожидание x:

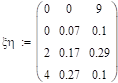
Дисперсия x:

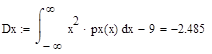
Плотность вероятностей y:

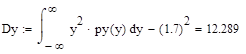
Математическое ожидание y:

Дисперсия y: