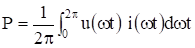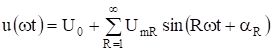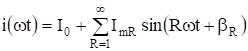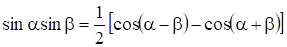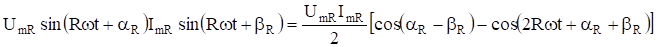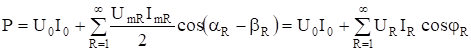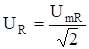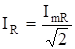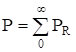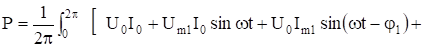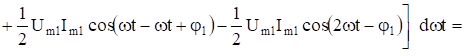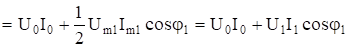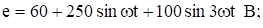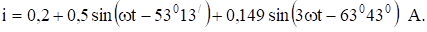Мощность в цепи периодического несипусоидального тока

В цепях несинусоидального тока строгий физический смысл имеет только активная мощность, определяемая как среднее за период значение произведения мгновенных значений тока и напряжения (мгновенной мощности).

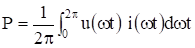
(13).

В том случае, когда известно разложение в ряд Фурье напряжения и тока цепи, можно определить активную мощность, выделяемую в цепи, через амплитуды и фазы всех гармонических составляющих напряжедия и тока.

Пусть заданы напряжение и ток.

Определим активную мощность цепи (13).

Для того, чтобы проинтегрировать произведение, целесообразно предварительно разложить это произведение на гармонические составляющие. При разложении учтем, что.

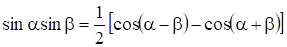
(14).

Таким образом, произведения напряжений и токов различных частот дадут периодические функции—косинусы—суммарной и разностной частоты, которые при интегрировании за период обратятся в нуль.

Произведения синусоидальных функций одинаковых частот дадут выражение.

При интегрировании за период пернодические функции с частотойобратятся в нуль. Следовательно, после интегрирования по формуле (13) произведения мгновенных значений напряжения и тока, получим выражение для активной мощности.

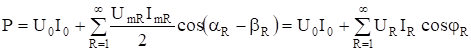
(15).

где постоянные составляющие;

.

— действующие значения Rй гармоники напряжения и тока, разность фаз R-й гармоники напряжения и тока.

Таким образом, активная мощность в цепи несинусоидального тока равна сумме активных мощностей всех гармоник в отдельности.

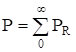
(16).

то есть Поясним сказанное на простом примере.

Пример 6. Известны напряжение и ток цепи Определить активную мощность.

Решение Вычислим активную мощность цепи по (13). При вычислении учтем тригонометрическое соотношение (14).

.

Полученная мощность соответствует уравнению (16).

Пример 7. Определить активную мощность, отдаваемуюисточником ЭДС в схеме рис. 2., параметры которой приведены в примере 3.

Решение При решении воспользуемся результатом, полученным в примере 3.

Активную мощность вычислим по формуле (15).