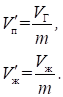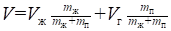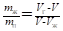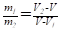Равновесие жидкости и насыщенного пара

Рассмотрим процесс сжатия вещества при постоянной температуре. Первоначально вещество предполагается газообразным. Вначале, по мере уменьшение объема, давление газа будет расти (рис. 1.9). По достижении объема V_г давление перестает изменяться, а вещество перестает быть однородным — часть газа конденсируется в жидкость. Происходит расслоение вещества на две фазы: жидкую и газообразную. По мере дальнейшего уменьшения объема всё большая часть вещества переходит в жидкую фазу, причем переход осуществляется при постоянном объеме р_{н. п (}давление насыщенного пара). После того как процесс конденсации заканчивается (это происходит при достижении объема V_ж), дальнейшее уменьшение объема начинает сопровождаться быстрым ростом давления.

На рис. 1.9 V_г есть объем, занимаемый веществом в газообразном состоянии при давлении р_{н. п}, V_ж — объем вещества в жидком состоянии при том же давлении. При любом промежуточном значении объема часть вещества с массой m_ж будет находиться в жидком, а m_п — в парообразном состоянии. Найдем отношение. Назовем удельным объемом объем единицы массы вещества. Тогда, если масса вещества равна m, удельные объемы насыщенного пара и жидкости при давлении насыщенного пара будут равны:

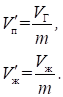
(1.76).

В состоянии, при котором масса жидкой фазы равна m_ж, а масса пара m_п, на долю жидкости будет приходиться объем V'_ж m_ж, а на долю насыщенного пара — объем V'_п m_п. В сумме оба эти объема должны быть равны объему V

V=V'_ж m_ж+V'_п m_п.

Подставив сюда выражение (1.76) для удельных объемов и заменив массу m суммой m_ж + m_п получим:

.

отсюда.

. (1.77).

Таким образом, отношение масс жидкости и насыщенного пара в двухфазном состоянии равно отношению отрезков, на которые делит горизонтальный участок изотермы точка, изображающая состояние.

Отметим, что при температурах, далеких от критической, различий между объемами жидкости и пара бывает намного больше. Например, удельный объем насыщенного водяного пара при 100? C в 1600 раз превышает удельный объем жидкой воды при той же температуре.

Итак, на диаграмме состояниям равновесия между жидкостью и насыщенным паром соответствует горизонтальный участок изотермы. Этот результат является общим для всех двухфазных состояний. Соотношение, аналогичное (1.77), имеет вид:

(m₁ и m_2 — массы вещества в первой и второй фазах).