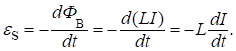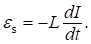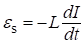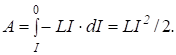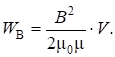Явление возникновения э.д.с. в том же проводнике, по которому течёт переменный ток, называют самоиндукцией, а саму э.д.с. э.д.с. самоиндукции. Возникновение э.д.с. самоиндукции объясняется следующим. Переменный ток, проходящий по проводнику, порождает вокруг себя переменное магнитное поле, которое, в свою очередь, создаёт магнитный поток, изменяющийся со временем, через площадь, ограниченную проводником.
Согласно явлению электромагнитной индукции, это изменение магнитного потока и приводит к появлению э.д.с. Значение э.д.с. самоиндукции найдём, подставляя выражение (1) в закон электромагнитной индукции (см. (14) лекцию № 9) и полагая, что L = const:
Итак,.
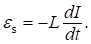
(4).
Итак, э.д.с. самоиндукции в проводнике пропорциональна скорости изменения силы тока, текущего по нему.
Под действием э.д.с. самоиндукции создаётся индукционный ток, называемый током самоиндукции.
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
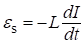

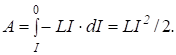
Пусть в электрической цепи (рис. 1) протекает постоянный ток силой I. Если отключить источник тока и замкнуть цепь (переключатель П перевести в положение 2), то в ней некоторое время будет течь убывающий ток, обусловленный э.д.с. самоиндукции s, равной. Элементарная работа, совершаемая э.д.с. самоиндукции по переносу по цепи элементарного заряда dq = Idt, равна Сила тока изменяется от I до 0. Поэтому, интегрируя это выражение в указанных пределах, получаем работу, совершаемую э.д.с. самоиндукции за время, в течение которого происходит исчезновение магнитного поля: Совершение этой работы сопровождается нагреванием проводника и окружающей среды и исчезновением магнитного поля, которое первоначально существовало вокруг проводника. Поскольку никаких других изменений в окружающей среде не происходит, то можно заключить, что магнитное поле обладает энергией, за счёт которой и совершается работа. Итак, энергия магнитного поля, существующего вокруг проводников с током, равна.
WB = LI2/ 2. (5).
Выразим энергию магнитного поля через величины, характеризующие само поле. Проделаем это на примере соленоида. Из формул (2) и (3) I = B/(0n) и L =0 n2V. Подставляя эти выражения в (5), получаем, что.
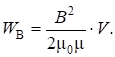
(6).
Магнитное поле внутри соленоида однородное (= const). Поэтому объёмная плотность энергии wB магнитного поля, т. е. энергия единицы объёма поля, внутри соленоида равна.
wB = WB/V = B2 /(20). (7).
Эта формула справедлива и в случае неоднородных статических и переменных магнитных полей.