Оценка величины погрешности линейного однофакторного уравнения

Обозначим разность между фактическим значением результативного признака и его расчетным значением как :

.

где.

фактическое значение y;

расчетное значение y,

— разность между ними.

В качестве меры суммарной погрешности выбрана величина:

.

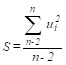
Для нашего примера S = 0.432.

Поскольку (среднее значение остатков) равно нулю, то суммарная погрешность равна остаточной дисперсии:

Остаточная дисперсия находится по формуле:

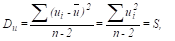
Для нашего примера. Можно показать, что.

.

Если то.

то.

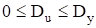
Таким образом, .

Легко заметить, что если.

то Это соотношение показывает, что в экономических приложениях допустимая суммарная погрешность может составить не более 20% от дисперсии результативного признака .

Стандартная ошибка уравнения находится по формуле:

где.

— остаточная дисперсия. В нашем случае .

Относительная погрешность уравнения регрессии вычисляется как:

.

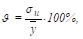
где стандартная ошибка; - среднее значение результативного признака.

В нашем случае = 7.07%.

Если величина мала и отсутствует автокорреляция остатков, то прогнозные качества оцененного регрессионного уравнения высоки.

Стандартная ошибка коэффициента b вычисляется по формуле:

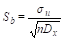
В нашем случае она равна .

Для вычисления стандартной ошибки коэффициента a используется формула:

В нашем примере .

Стандартные ошибки коэффициентов используются для оценивания параметров уравнения регрессии.

Коэффициенты считаются значимыми, если.

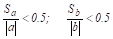
В нашем примере.

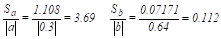
Коэффициент а не значим, т.к. указанное отношение больше 0.5, а относительная погрешность уравнения регрессии слишком высока — 26.7%.

Стандартные ошибки коэффициентов используются также для оценки статистической значимости коэффициентов при помощи t — критерия Стьюдента. Значения t — критерия Стьюдента содержатся в справочниках по математической статистике. В таблице 1.3 приводятся его некоторые значения.

Далее находятся максимальные и минимальные значения параметров () по формулам:

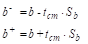
Таблица 1.3 Некоторые значения t — критерия Стьюдента.

Для нашего примера находим:

Если интервал () достаточно мал и не содержит ноль, то коэффициент b является статистически значимым на с — процентном доверительном уровне.

Аналогично находятся максимальные и минимальные значения параметра а. Для нашего примера:

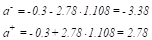
Коэффициент а не является статистически значимым, т.к. интервал () велик и содержит ноль.

Вывод: полученные результаты не являются значимыми и не могут быть использованы для прогнозных расчетов. Ситуацию можно поправить следующими способами:

• а) увеличить число n;
• б) увеличить количество факторов;
• в) изменить форму уравнения.

Проблема автокорреляции остатков. Критерий Дарбина-Уотсона

Часто для нахождения уравнений регрессии используются динамические ряды, т. е. последовательность экономических показателей за ряд лет (кварталов, месяцев), следующих друг за другом.

В этом случае имеется некоторая зависимость последующего значения показателя, от его предыдущего значения, которое называется автокорреляцией. В некоторых случаях зависимость такого рода является весьма сильной и влияет на точность коэффициента регрессии.

Пусть уравнение регрессии построено и имеет вид:

— погрешность уравнения регрессии в год t.

Явление автокорреляции остатков состоит в том, что в любой год t остаток не является случайной величиной, а зависит от величины остатка предыдущего года. В результате при использовании уравнения регрессии могут быть большие ошибки.

Для определения наличия или отсутствия автокорреляции применяется критерий Дарбина-Уотсона:

.

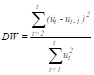
Возможные значения критерия DW находятся в интервале от 0 до 4. Если автокорреляция остатков отсутствует, то DW2.