Классическое определение регрессии

Понятие регрессии результирующего показателя по объясняющим переменным является базовым в регрессионном анализе. Функция f (X), описывающая изменение условного среднего значения результирующего показателя в зависимости от изменения заданного значения Х предикторной переменной называется функцией регрессии.

Оптимизационный подход в регрессионном анализе

Точного описания функции регрессии f (X) в статистической практике никогда не имеется, поэтому ограничиваются поиском подходящих аппроксимаций для, основанных на статистических данных вида (4.1). Значит необходимо уметь измерять качество предполагаемой аппроксимации искомой функции регрессии f (X) с помощью. Для этого в теории и практике статистического исследования зависимостей используют функциирегрессии, являющиеся наилучшими прогностическими моделями для анализируемого результирующего показателя в смысле минимизации заданного критерия адекватности .

• 1. Пусть — неотрицательная монотонно неубывающая функция потерь, измеряющая неточность восстановления с помощью, u=-.
• 2. Введем критерий адекватности модели и, используемых для восстановления : — усреднение по всем возможным значениям ошибки при каждом фиксированном X.

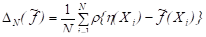
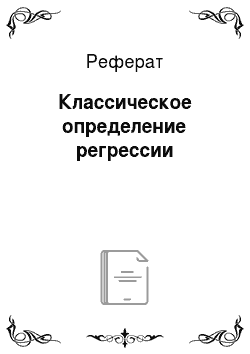
Его выборочный аналог: — усреднение по имеющимся наблюдениям.

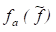
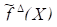
3. Зададимся классом допустимых решений F, в рамках которого будем вести поиск наилучшей в смысле критерия (или) аппроксимации для. Если при этом некоторое параметрическое семейство функций, то задача подбора сводится к определению, для которого некоторая характеристика точности восстановления является наилучшей. 4. Будем называть функцию функциейрегрессии, если она дает прогноз для условных значений результирующего показателя, являющегося наилучшим в смысле критерия адекватности.

В практике статистического исследования зависимостей чаще всего используют функции потерь следующего вида:

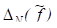
=. Получаемая с помощью (7.1) регрессия называется среднеквадратической, а метод, реализующий минимизацию функционала — методом наименьших квадратов.

=. Получаемая с помощью (7.1) регрессия называется среднеабсолютной (медианной), а метод, реализующий минимизацию функционала — методом наименьших модулей.

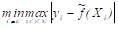
=. Минимизация сводится к поиску, поэтому регрессия называется минимаксной.

Таким образом, наиболее распространенными случаямирегрессии являются среднеквадратическая, медианная и минимаксная регрессии.

Соотношение истинной f (X), теоретической аппроксимирующей и выборочной аппроксимирующей регрессий существенно зависит от выбора критерия адекватности (определяемого природой регрессионных остатков) и класса допустимых решений F. В частности, даже при удачном выборе критерия адекватности в ситуациях, когда истинная функция регрессии f (X) не накрывается классом допустимых решений F, выборочная аппроксимирующая функция регрессии не будет стремиться к истинной при неограниченном росте объема выборки.