Стратегия синтеза алгоритма решения задачи

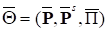
Принятая модель алгоритма определяет итеративную стратегию синтеза алгоритмов, которая сводится к преобразованию исходной модели =(P, P^s, П), приводящему к цели в виде оптимальной модели корректного алгоритма, путем итерационного пересчета параметров модели до схождения.

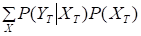
Постановка задачи. Известна наблюдаемая величина y (t) в виде последовательности Y_T=y₀, y₁,…, y_Т-1 длины Т, порождаемая последовательностью O=o₁o₂…o_T. Вероятность наблюдать y (t) равна P (Y_T)=, где сумма задаётся по всем возможным скрытым переменным x (t) в виде последовательности скрытых узлов X_T=x₀, x₁,…, x_Т-1. По имеющимся данным y (t) необходимо определить скрытые параметры наиболее вероятной последовательности состояний марковской цепи S=s_i1…s_iT.

Решение сформулированной задачи может быть достигнуто за три этапа, каждый из которых реализуется известным алгоритмом.

Первый этап: За T шагов в модели =(P, P^s, П) порождается последовательность наблюдений O_1,T=o₁,…, o_T, причем в момент t для состояния s: X_i=i вероятность P (O₁,_t-₁X_t=s) того, что во время переходов образовалась последовательность наблюдений O_1,t-₁, а P (O_{t, T}X_t=s) — вероятность того, что после этого состояния наблюдается последовательность наблюдений O_{t, T}.

Ищется вероятность P (X_t=sO)=P (X_t=sO₁,_t-₁O_{t, T}) того, что в момент t цепь будет в состоянии s.

1. Для произвольного состояния s в произвольный шаг t вероятность P (O1,tXt=si) того, что на пути к нему была произведена последовательность O1, t для следующих t можно вычислить рекуррентно:

P (O1,tXt=si)=.

=.

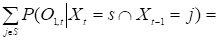
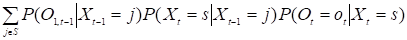
Вероятность попасть в состояние s на t-ом шаге, учитывая, что после перехода произойдет событие o_t будет равна вероятности быть в состоянии j на t-ом шаге, умноженной на вероятность перейти из состояния j в s, произведя событие o_t для всех jS.

2. Вероятность того, что после произвольного состояния s будет произведена последовательность Ot+1,T определяются рекуррентно:

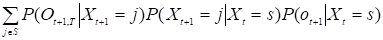
P (O_{t, T}X_t=s)=.

3. Чтобы найти вероятность того, что будет произведена цепочка событий, P (O), нужно просуммировать произведение обеих вероятностей для всех состояний при произвольном шаге t:

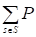
P (O)=(O_1,tX_t=s)P (O_{t, T}X_t=s),.

а поскольку будущее марковской цепи не зависит от прошлого и вероятность наблюдения события O_t не зависит от прошлых наблюдений последовательности O_1,t-1, то вероятность того, что в момент t цепь будет в состоянии s:

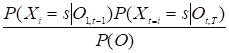
P (X_t=sO)=P (X_t=sO₁,_t-1O_{t, T})=.

Данная задача решается с помощью алгоритма «вперед-назад» [9−11], который позволяет найти в скрытой марковской модели вероятность попадания в состояние s на t-ом шаге при последовательности наблюдений O и (скрытой) последовательности состояний X.

Второй этап: По заданной HMM с пространством состояний S={s₁, s₂,…, s_K}, начальными вероятностями _i нахождения в состоянии i и вероятностями P_{i, j} перехода из состояния i в состояние j, по наблюдаемым y₁,…, y_T и множества исходных информаций J_in ищется «оптимальная» наиболее правдоподобная последовательность состояний скрытых узлов S=s₁…s_T (путь Витерби), наиболее точно описывающую данную модель. Тогда наиболее вероятная последовательность состояний x₁,…, x_T задается рекуррентными соотношениями:

V_1,k=P (y₁k)_k, V_{t, k}=P (y_tk), (2).

где V_{t, k} — вероятность наиболее правдоподобной последовательности состояний, ответственной за появление первых t наблюдаемых символов, завершающейся в состоянии k. Путь Витерби ищется по состояниям x, удовлетворяющих уравнению (2), т. е.

x_T=.

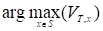
x_t-₁=.

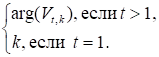
Для решения данной задачи используют алгоритм Витерби (Andrew Viterbi, 1967 год), позволяющего на основе последовательности наблюдений получить наиболее правдоподобную последовательность скрытых состояний (путь Витерби) скрытой марковской модели [12−15].

Третий этап: По заданной выходной последовательности наблюдений O определяются неизвестные параметры HMM, максимизирующие вероятность наблюдений O.

^*=.

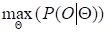
Причем число моментов времени r, в которых осуществляются наблюдения, устанавливается заранее и состоит из следующих шагов:

• 1) определение всех последовательностей состояний модели S_i={s_i1,…, s_ir}, i=1,…, r проблеморазрешающей системы в заданные моменты времени;
• 2) оценка вероятностей P (S_i) появления для каждой последовательности S_i, i=1,…, r, выявленной на предыдущем шаге, путём вычисления произведений вероятностей переходов между состояниями модели в течение интервалов, ограниченных установленными контрольными моментами времени, а именно:

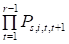
P (S_i)=,.

где P_{s, i, t, t+1}-вероятность перехода из состояния s_it, в котором система пребывала в момент времени t, в состояние s_{i, t+1}, занятого в момент t+1;

3) вероятность появления наблюдаемой последовательности X={x₁,…, x_r} для последовательностей состояний S_i, i=1,…, r.

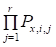
P_ix=P (S_i),.

где P_{x, i, j}-вероятность получения наблюдаемой характеристики x_j при состоянии s_ij;

4) выбор наиболее вероятной последовательности состояний S_max{S_i}_{i=1,…, r}, соответствующей наибольшей вероятности.

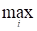
{P}_{x, max}=P_{ix i =1,…, r}.

Данный этап стратегии реализуется алгоритмом Баума-Велша (Baum — Welch algorithm) [10, 16].