Моделирование распределения поля в магнитных системах электротехнических устройств с использованием нелинейных многополюсников

Аннотация

Рассматривается задача моделирования распределения магнитного поля в магнитопроводах электротехнических устройств с целью оценки их характеристик в режимах эксплуатации. Проблема сводится к решению краевой задачи для уравнения эллиптического типа в ферромагнитной среде с нелинейными характеристиками. Для расчета предложено использовать блочные элементы в виде многоугольников произвольной конфигурации, которые рассматриваются как нелинейные многополюсники. Вебер-амперные характеристики многополюсников находятся в результате решения краевых задач для многоугольников, образующих блочные элементы.

Краевые задачи решаются с использованием комплексного метода граничных элементов, что обеспечивает прямое нахождение уравнений связи между магнитными напряжениями и потоками многополюсников.

Нелинейность характеристик учитывается по найденному в результате расчета распределению поля на границе многополюсников путем корректировки магнитных проницаемостей блочных элементов, которая выполняется итерационно.

Ключевые слова: электротехническая система, магнитная цепь, краевая задача, блочный элемент, многополюсник, комплексный граничный элемент, матрица проводимостей.

Методы теории цепей широко используются для моделирования различных технических систем [1,2]. Так, схемы замещения магнитопроводов электротехнических устройств применяются для анализа распределения поля в их элементах [1,2], особенно на этапах проектирования или оптимизации, когда возникает необходимость выполнения многовариантных расчетов. При этом на точность расчетов существенное влияние оказывает выбранная топология схемы замещения и магнитные характеристики ее элементов, которые при насыщении электротехнической стали в реальных режимах эксплуатации описываются нелинейными зависимостями.

Сложившиеся подходы к построению схем замещения не являются формализованными, в основном основываются на эвристических допущениях о характере пространственного распределения поля в магнитных системах. Это не только ограничивает возможности применения магнитных цепей для моделирования распределения поля в магнитопроводах электротехнических систем, но и делает проблематичным такое приближение в тех случаях, когда локальное перемагничивание стали носит пространственный характер.

Ниже описан формализованный подход к построению схем замещения магнитопроводов электротехнических устройств с помощью нелинейных многополюсников, которые могут быть использованы для приближенного анализа распределения магнитного поля при любых режимах локального перемагничивания.

Рассмотрим следующую типовую задачу, к решению которой сводится расчет поля в магнитных системах. Пусть область на плоскости с границей (рис.1) заполнена ферромагнитной средой с нелинейными характеристиками, которые задаются магнитной проницаемостью. При этом.

.

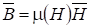
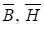
где — индукция и напряженность магнитного поля соответственно.

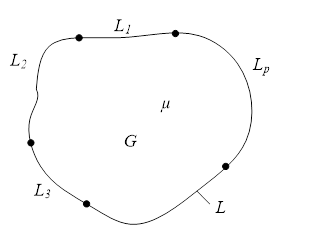
Рис. 1. — Расчетная область

Тогда магнитное поле в области описывается системой уравнений.

;;. (1).

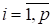
Будем считать, что на участках, , границы области известна либо касательная составляющая напряженности магнитного поля, либо нормальная составляющая индукции :

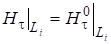
;; (2).

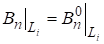
;, (3).

Где магнитопровод уравнение эллиптический блочный.

 — известные на участках границы функции.

В дополнение к граничным условиям (2), (3) будем считать заданными магнитные потоки через участки границы, на которой задана напряженность поля:

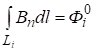
(4).

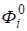
где — известные значения магнитного потока через соответствующие участки границы .

Заметим, что на границе L области выполняются следующие соотношения:

;

.

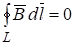
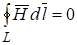
Поэтому условия (2), (3) и последние равенства должны быть согласованы.

Для моделирования распределения поля в области будем использовать блочные элементы [8,9], которые строятся с использованием двух допущений, характерных для расчета поля в нелинейных средах. Блочным элементом в дальнейшем будем называть любой многоугольник, расположенный в области, в пределах которого поле меняется так, что магнитную проницаемость в его отдельных точках можно считать постоянной. Заметим, что такая линеаризация является стандартным приемом при численных расчетах физических полей в нелинейных средах.

С учетом уравнений (1) при принятом допущении, магнитное поле в каждом многоугольном элементе разбиения с границей описывается системой уравнений:

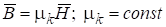
;;. (5).

При этом на общих участках границ элементов, должны выполняться условия сопряжения.

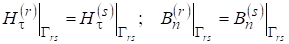
(6).

где в левой и правой частях приводятся предельные значения касательной составляющей напряженности и нормальной компоненты индукции со стороны элементов, соответственно.

С учетом уравнений (5) поле в каждом элементе разбиения можно описать с помощью двух потенциалов или, равных:

.

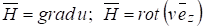
При этом оба потенциала в области являются гармоническими функциями и на общих участках границы удовлетворяют условиям.

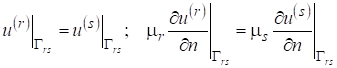
; (7).

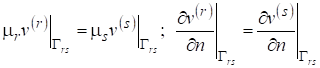
. (8).

Каждому блочному элементу с границей поставим в соответствие многополюсник так, как это показано на рис. 2.

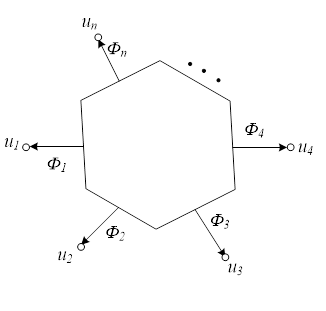
Рис. 2. — Блочный элемент, совмещенный с многополюсником

Опишем алгоритм нахождения матриц проводимостей и сопротивлений, связывающих магнитные потоки поля.

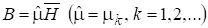
через сечения, совпадающие с ребрами, с магнитными потенциалами, определяемыми через поле. Уравнения связи зададим равенствами:

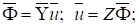
(9).

.

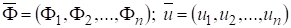
Заметим, что введенные магнитные потенциалы u, v являются сопряженными функциями.

Поэтому их можно рассматривать как действительную и мнимую части некоторой аналитической в области функции комплексного переменного:

. (10).

При этом гармоническая функция u(x, y), определена с точностью до постоянного слагаемого, а все функции v(x, y), сопряженные с функцией u(x, y), также могут отличаться только на постоянную [9,10]. Обеспечивая единственность решения, достаточно положить в каких-либо двух точках M, NГ:

. (11).

Для аналитической однозначной функции (10) в односвязной области справедлива интегральная формула Коши [10]:

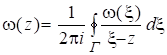
(12).

где направление обхода контура Г выбрано таким образом, что при обходе контура область остается слева.

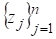
Введем в комплексной плоскости z, систему узлов, где n — число узлов на контуре Г. Пронумеруем узлы последовательно, начиная с единицы в положительном направлении обхода контура Г, при котором область остается слева. На контуре Г определим n граничных элементов, следующими соотношением [9]:

.

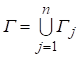
Где.

;; ,.

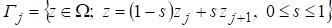
причем нумерация граничных элементов соответствует нумерации узлов.

Функцию на границе Г аппроксимируем кусочно-линейной функцией вида.

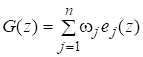
(13).

где.

.

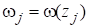
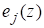
а базисная функция, соответствующая узлу, определяется равенством.

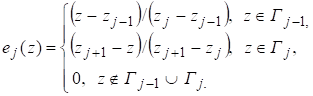
(14).

Из выражения (14) следует, что функция G(z) на Г является непрерывной и.

.

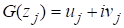
где , — значения магнитных потенциалов в узле. Подставляя функцию (13) в интегральную формулу Коши (12), получим:

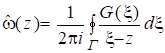
(15).

где z — внутренняя точка области (zГ). Функция является аппроксимирующей для функции в области с погрешностью, обусловленной приближением функции кусочно-линейной функцией (13) на границе Г. С учетом (13) выражение (15) для можно записать следующим образом:

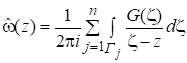
zГ, z. (16).

На каждом элементе функция G(z) задается равенством:

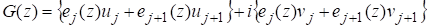
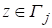
. (17).

Используя соотношения (17) и (14), найдем интеграл в равенстве (16) по каждому элементу :

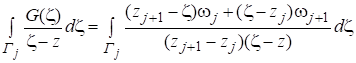
z, zГ. (18).

После вспомогательных преобразований, получим из формулы (18).

;

;

.

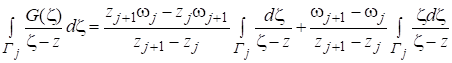
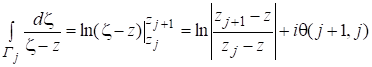
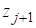
где — угол между лучами, соединяющими узлы и с точкой z рис. 3. Запишем интеграл (18) в виде:

.

.

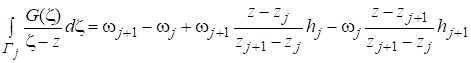
Подставив полученные выражения в формулу (16), получим.

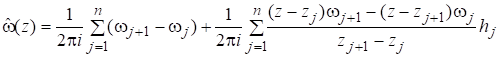
(19).

где принято,. Тогда первая сумма в равенстве (19) равна нулю и, поэтому.

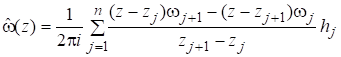
. (20).

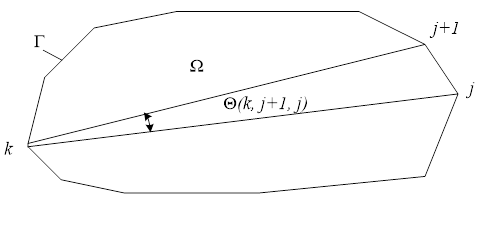
Рис. 3. — К вычислению интеграла по контуру Г

Равенство (20) задает аппроксимирующую функцию (15) во внутренних точках области через узловые граничные значения комплексного потенциала .

Для определения величин, поступим следующим образом. Внутреннюю точку z области устремим к узлу, , тогда, переходя к пределу в левой и правой части равенства (20), получим:

.

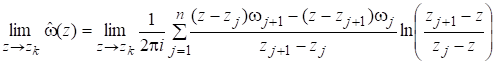
Находя предел в последнем выражении, имеем.

.

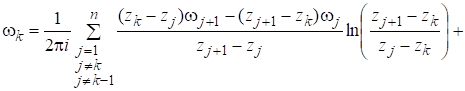
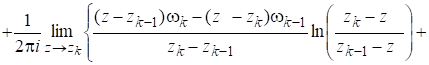
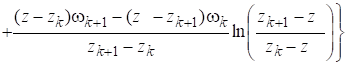
Упростив выражение, стоящее в скобках последнего равенства, получим:

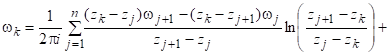
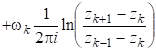
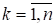
. (21).

Уравнения (21) после разделения в них действительной и мнимой части можно записать в виде:

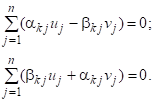
(22).

При этом систему (22) необходимо дополнить уравнениями (11).

Для определения матрицы проводимостей (9) будем находить решение системы (22) при значениях потенциалов узлов равных.

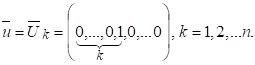
Отметим, что система уравнений (22) имеет число уравнений, в два раза превышающее число неизвестных. Поэтому для решения этой системы используется метод наименьших квадратов.

По найденным узловым значениям потенциала находятся потоки через ребра многоугольника.

Так, если к ребру с потоком примыкают вершины (узлы) с потенциалами, то поток через него равен.

.

В результате расчетов при каждом заданном распределении потенциалов узлов определяется k-й столбец матрицы и далее сама матрица. Матрица находятся аналогично.

После определения уравнений связи многополюсников (9), соответствующих блочным элементам разбиения, выполняется анализ распределения потоков в магнитных системах исследуемых устройств. При этом условия на границе расчетной области для нормальной составляющей индукции позволяют задать часть потоков через участки блочных элементов, примыкающие к границе. Учет граничного условия относительно касательной составляющей напряженности обеспечивается соответствующим заданием разности магнитных потенциалов для узлов многополюсника, совмещенных с границей. Выполнение условия непрерывности поля на общих участках границы соседних блочных элементов обеспечивается в слабой форме путем приравнивания потенциалов общих узлов и потоков магнитной индукции через общие участки границы, вычисленных в примыкающих областях разбиения с разными магнитными проницаемостями.

Нелинейность характеристик учитывается за счет того, что проницаемости в областях разбиения уточняются итерационно по значениям напряженности, получаемым в результате расчета. Для этого используется ее среднее значение напряженности на границе каждого элемента разбиения, которое приближенно может быть оценено по найденному распределению потенциалов и потоков в многополюсниках. Отметим, что матрицы многополюсников находятся однократно и корректировке не подлежат.

• 1. Носков В. Н., Пустоветов М. Ю. Компьютерное моделирование режима холостого хода электромеханического расщепителя фаз на базе трехфазного асинхронного электродвигателя// Инженерный вестник Дона, 2016, № 2 URL: ivdon.ru/ru/magazine/archive/n2y2016/3633/.
• 2. Пивнев В. В., Басан С. Н. Математическое моделирование нелинейных характеристик элементов применительно к задаче реализации двухполюсников с заданными нелинейными зависимостями// Инженерный вестник Дона, 2016, № 4 URL: ivdon.ru/ru/magazine/archive/n4y2016/3857/.
• 3. Нго Фыонг Ле, Гульков Г. И. Эквивалентная схема магнитной цепи синхронного двигателя с инкорпорированными магнитами. Энергетика, 2015, № 4. c. 13−24.
• 4. Miller T.J.E. Brushless Permonent-Magnet and Relactance Motor Drives. Oxford: Clarendon Press, 1989. pp. — 207.
• 5. Булыжев Е. М., Меньшов Е. Н., Джавахия Г. А. Оптимизация магнитного сепаратора. — Известия Самарского центра РАН, т.13, № 4, 2015. с. 111−116.
• 6. Носов Г. В., Лусс А. А. Расчет внешнего магнитного поля рельслтронов. Фундаментальные исследования. 2013. № 10. с. 3363−3367.
• 7. Буль О. Б. Методы расчета магнитных систем электрических аппаратов: Магнитные цепи, поля и программа FEMM. М.: Издательский центр «Академия», 2005. 336 c.
• 8. Ткачев А. Н., Клименко В. В. Метод сопряженных потенциалов для расчета двухмерных электрических и магнитных полей: монография. Юж.-Рос. гос. техн. ун-т. Новочеркасск: ЮРГПУ (НПИ), 2012. 172 c.
• 9. Tkachev А., Pashkovskiy А., Burtceva О. Application of block elements method for a calculation of the magnetic field and force characteristics in electromechanical systems. Vol. 129: International Conference on Industrial Engineering (ICIE 2015). Procedia Engineering. 2015. pp. 288−293.
• 10. T. Hromadko, C. Lai, The Complex Variable Boundary Element Method in Engineering Analysis, Springer Vergas New York Inc, 1987. pp. 303.

References.

• 1. Noskov V.N., Pustovetov M.Ju. Inzhenernyj vestnik Dona (Rus), 2016, № 2 URL: ivdon.ru/ru/magazine/archive/n2y2016/3633/.
• 2. Pivnev V.V., Basan S.N. Inzhenernyj vestnik Dona (Rus), 2016, № 4 URL: ivdon.ru/ru/magazine/archive/n4y2016/3857/.
• 3. Ngo Fyong Le, Gul’kov G.I. Jenergetika, 2015, № 4. pp. 13−24.
• 4. Miller T.J.E. Brushless Permonent-Magnet and Relactance Motor Drives. Oxford: Clarendon Press, 1989. pp. 207.
• 5. Bulyzhev E.M., Men’shov E. N., Dzhavahija G.A. Izvestija Samarskogo centra RAN, t.13, № 4, 2015. pp. 111−116.
• 6. Nosov G.V., Luss A.A. Fundamental’nye issledovanija. 2013. № 10. pp. 3363−3367.
• 7. Bul' O.B. Metody rascheta magnitnyh sistem jelektricheskih apparatov: Magnitnye cepi, polja i programma FEMM [Methods for calculating the magnetic systems of electrical apparatus: Magnetic circuits, fields and the program FEMM]. — M.: Izdatel’skij centr «Akademija», 2005. 336 p.
• 8. Tkachev A.N., Klimenko V.V. Metod soprjazhennyh potencialov dlja rascheta dvuhmernyh jelektricheskih i magnitnyh polej: monografija [The method of conjugate potentials for the calculation of two-dimensional electric and magnetic fields: monograph]. Juzh.-Ros. gos. tehn. un-t. Novocherkassk: JuRGPU (NPI), 2012. 172 p.
• 9. Tkachev А., Pashkovskiy А., Burtceva О. Application of block elements method for a calculation of the magnetic field and force characteristics in electromechanical systems. Vol. 129: International Conference on Industrial Engineering (ICIE 2015). Procedia Engineering. 2015. pp. 288−293.
• 10. T. Hromadko, C. Lai, The Complex Variable Boundary Element Method in Engineering Analysis, Springer Vergas New York Inc, 1987. pp. 303.