Обзор литературы. 
Исследование волноводной нагрузки с магнитной стенкой на грибовидном метаматериале

В связи с возрождением интереса к искусственным периодическим структурам, начина с 2000;х годов количество публикаций и работ в направлении данной тематики неуклонно растет. Ученые активно ищут наиболее удачные конструкции метаматериалов для конкретного практического применения, новые области, где можно внедрить данные структуры. Однако, несмотря на все это многообразие, работ по применению метаматериалов в конструкциях волноводов прямоугольного сечения относительно немного. Еще более сужают круг поиски трудов по использованию искусственных материалов в качестве волноводной нагрузки. Но все же исследования в данной области ведутся как в России, так и за рубежом.

Если обратиться сначала к зарубежным изданиям, то среди множества публикаций по метаматериалам выделяется книга Н. Энгеты и Р. В. Циолковского «Метаматериалы. Применение в физике и инженерии» [2]. В данной работе приведено исчерпывающее описание исключительных свойств метаматериалов: отрицательных значений диэлектрической и магнитной проницаемости, коэффициента преломления, представлены различные конструктивные исполнения метаматериалов совместно с их характеристиками. Особого внимания заслуживает описание грибовидного метаматериала, так как подобная структура будет использована и в данной работе. Рассматриваемое решение является высокоимпедансной поверхностью, образованной периодически распределенными металлическими элементами на единой металлической подложке. Указывается, что подобная конструкция может быть рассмотрена как полосно-заграждающая, аналогично фотонным кристаллам. Приводятся методы расчета параметров элементарной ячейки, таких как сопротивление, емкость и индуктивность, а также способы построения поверхности с регулируемыми параметрами.

Однако все рассматриваемые в книге варианты практического применения грибовидных метаматериалов относятся исключительно к сфере антенной техники, и не рассматривается возможность их применения в качестве волноводной нагрузки.

Имеет смысл рассмотреть статью «Уменьшение размеров волноводов при использовании метаматериалов с отрицательной магнитной проводимостью» ученых из Хорватии: С. Хабара, Ю. Бартоли и З. Сипуса [13]. Здесь изучено и практически подтверждено явление распространения обратной электромагнитной волны в волноводе на частоте ниже резонансной. Для объяснения происходящих процессов представлена модель линии распространения электромагнитных волн в волноводе и влияние различного типа метаматриала на конфигурацию этой модели. Стоит подчеркнуть, что рассматриваемый метаматериал являлся планарным и имел форму протяженной пластики с двойными кольцами, вводимой в волновод вдоль его длины.

Впервые грибовидный материал представил в своей диссертации по теме «Высокоимпедансные электромагнитные поверхности» Д. Ф. Сивенпайпер [17]. Он подробно описал свойства высокоимпедансных поверхностей и привел технологию изготовления подобной структуры трехмерного метаматериала. Автор также указал, что распространение по поверхности поперечной электрической волны зависит от частоты: на определенных частотах волна распространяться не может. В работе дается информация касательно двух типов поверхностей: емкостной и индуктивной и модели конечного элемента, используемой в численных расчетах периодических структур. С другой стороны, в диссертации нет примеров практического применения грибовидного метаматериала кроме как поверхности, улучшающей направленность антенн.

Другой интересной работой в затронутой области можно считать статью китайских ученых Л. Ли, Б. Ли, Х. Лиу и Ч. Лианга под названием «Модель элементарной резонансной ячейки для полосно-пропускающих структур» [14]. В работе подробно рассматривается модель элементарной резонансной ячейки метаматериала, выполненного в форме грибовидной периодической структуры. Приводятся картины двух вариантов резонансных мод, существующих в описываемом метаматериале: монополяризованной и кросс-поляризованной. Также описываются проведенные численные эксперименты с использованием структуры в качестве нагрузки прямоугольного волновода, с применением коаксиального зонда для определения коэффициента отражения, по построению низкопрофильной обратной антенны на основе подложки из метаматериала. Данное исследование выгодно выделяется на фоне других тем, что содержит информацию о влиянии параметров элементарной ячейки (высоты ножки «гриба» и ее диаметра, расстоянии между шляпками «грибов») искусственной периодической среды на резонансную частоту монополяризованной моды и диэлектрическую проницаемость структуры в целом. Как и в работе, описанной выше, приводятся различные возможные конфигурации структурных единиц метаматериала с шестиугольными и треугольными внешними поверхностями.

Стоит отметить, что недостатком данной публикации является отсутствие каких-либо сведений о возможном практическом применении рассматриваемой конструкции волноводной нагрузки. Интересно было бы узнать и об изменении характеристик устройства при вариации параметров, например, удаленности нагрузки от конца волновода, или при заполнении погружении элементов метаматериала в диэлектрик.

Отечественная библиография начинается со статьи В. Г. Веселаго «Электродинамика веществ с одновременно отрицательными значениями е и м». Работа была опубликована в 1967 г. в журнале «Успехи физических наук», в ней ученый впервые выдвинул теорию о существовании материалов отрицательными значениями магнитной и диэлектрической проницаемостей, а также привел соответствующие математические выкладки и описал некоторые проявления электродинамики веществ с отрицательным показателем преломления. Несмотря на то, что данная работа была написана ровно полвека назад, на нее ссылаются многие современные ученые, так как теория Веселаго положила начало исследованию метаматериалов в принципе. Поэтому при работе в данном направлении необходимо, прежде всего, ознакомиться с теоретическим обоснованием исследуемого явления.

В направлении выбранной нами темы российскими исследователями написан ряд статей, опубликованных в сборнике А. Кухаренко и А. Елизарова «Практическое использование метаматериалов в конструкциях устройств СВЧ» [7]. Ценность источника для данной работы в том, что приводится подробное описание грибовидного метаматериала, варианты реализации подобной искусственной периодической структуры, примеры решений для расширения полосы запирания. Помимо прочего, каждая статья сборника содержит предложение по практическому применению описанного в ней решения, например, реализация частотно-селективного устройства, микрополосковой антенны, прямоугольного волновода с магнитной стенкой, чувствительного элемента с применением метаматериала. Важно отметить, что большинство статей посвящены изучению как раз грибовидной структуры, аналогичной варианту, используемому в текущей работе, так что по детальности ее рассмотрения сборник выгодно выделяется на фоне других публикаций.

К сожалению, прямоугольному волноводу с метаматериалом посвящена всего одна работа из данного сборника. Аналогично большинству приведенных выше публикаций, здесь отсутствует рассмотрение вопроса о применении грибовидного метаматериала в качестве нагрузки прямоугольного волновода.

Отдельного внимания заслуживает недавно опубликованная статья Д. А. Усанова, В. П. Мещанова, А. В. Скрипаля, Н. Ф, Попова, Д. В. Пономарева и М. К. Мерданова под названием «Согласованные нагрузки сантиметрового и миллиметрового диапазонов длин волн на СВЧ фотонных кристаллах» [12]. Как видно из названия, эта публикация посвящена конкретно созданию согласованной нагрузки прямоугольного волновода. Авторы приводят обоснование причины поиска нового решения для волноводной нагрузки, ссылаясь на недостатки габаритных и частотных показателей существующих конструкций. Описывается механизм работы СВЧ фотонных кристаллов — материалов, образованных несколькими слоями диэлектриков и металла с различной толщиной и показателями диэлектрической и электромагнитной проницаемости. На основе экспериментально полученных данных даже были изготовлены широкополосные волноводные согласованные нагрузки.

Однако данная работа также отклоняется от выбранной нами тематики в том, что используемая конструкция метаматериала представляет собой фотонный кристалл, а не грибовидную структуру. Таким образом, рассмотренная публикация может быть образцом количественных показателей, достигнутых при компьютерном моделировании. В итоге полезно будет провести сравнение двух предложенных вариантов согласованной нагрузки на метаматериалах различного конструктивного исполнения.

На основе проведенного обзора литературы можно сделать вывод, что выбранная тематика является актуальной в научной среде, исследуется не только в России, но и за рубежом. Количество различных решений, связанных с практическим применением метаматериалов в технике, велико, но область использования именно грибовидных структур в качестве согласованной волноводной нагрузки исследована недостаточно.

Цели и задачи

Основной целью данной работы является исследование волноводной нагрузки, выполненной из грибовидного метаматериала: получение на основе компьютерного моделирования количественных зависимостей коэффициента стоячей волны (VSWR) и коэффициента отражения (S₁₁), а также выбор наиболее выгодного конструктивного исполнения для достижения требуемых технических характеристик.

Для достижения поставленной цели необходимо решить ряд задач:

• 1. Разработать компьютерную модель волновода с нагрузкой в виде пластины с грибовидным метаматериалом.
• 2. Провести моделирование распространения электромагнитной волны основного типа (H₁₀) в широком диапазоне частот.

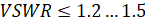
• 3. Определить участки с удовлетворительным значением коэффициента стоячей волны ().
• 4. Рассмотреть зависимость исследуемых характеристик от габаритных размеров конструкции и применяемых в грибовидной структуре магнитных покрытий.
• 5. Получить итоговые значения параметров конструкции для достижения лучших частотных показателей (ширины полосы согласования).