Линейные аппроксимационные модели хроматографических сигналов

Хроматограмма, формируемая хроматографическим прибором при выполнении анализа пробы вещества, представляет собой суперпозицию пиков определенной формы. Выходной сигнал хроматографического прибора представляет собой суперпозицию хроматографических пиков (ХП) S (t), соответствующих компонентам анализируемой смеси с наложением шума.

Форма ХП зависит от ряда факторов. Симметричные пики при прочих благоприятных условиях соответствуют стандартному режиму работы прибора, однако на практике это выполняется далеко не всегда. В хроматографии при симметричной форме пика наиболее распространена Гауссова модель, линейная относительно коэффициента А, определяющего его интенсивность:

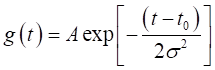
(1).

где t0 — время выхода вершины пика, у — параметр его ширины.

Такая модель изображена на рис. 1.

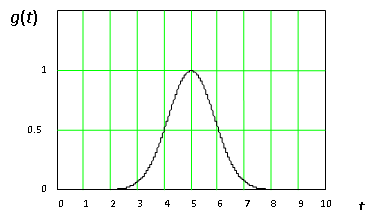
Рис. 1. — Основная модель аналитического пика g (t)

Асимметричные формы ХП описываются различными модификациями Гауссовой модели, например [1, 2]:

• — би — Гауссовой моделью,
• — комбинацией Гауссовой и экспоненциальной моделей,
• — сверткой нормальной и экспоненциальной моделей и др.

В практике хроматографических измерений часто оказывается важным не точное соответствие модели реальному пику, а возможность быстрого получения основных его параметров, таких, как площадь пика и время его выхода. Этим обусловлено широкое распространение не только наиболее простой из описанных моделей — Гауссовой, но и еще более упрощенных моделей, например, модели в виде треугольника [2, 3].

Что касается параметров сигнала, то, например, в газовой хроматографии (ГХ) они находятся в следующих диапазонах [1, 4]:

• — амплитуда пика, А = 10−6 … 10 В;
• — среднеквадратическая ширина пика = 0,2…100 с;
• — площадь пика S = 10 … 107 mkВ? с;
• — шум n (t) = 2…100 мкВ;
• — дрейф базисного сигнала y (t)/dt — -до 20 мВ/час;
• — время выхода пика — 10 с … 10 час.

Вышеприведенные значения параметров сигнала являются экстремальными, однако количество анализов со значениями экстремальных параметров составляет незначительную часть общего их числа. Так, например, в лабораториях предприятий по производству синтетического каучука количество анализов продолжительностью свыше 30 минут составляет 0,6% общего числа анализов [1]. На снижение времени анализа направлены усилия и разработчиков методик анализов (подбор режимов, выбор подвижной и неподвижной фаз, помещаемых в хроматографические колонки и т. п.) и конструкторов аппаратной части анализаторов (повышение чувствительности детекторов, устранение дестабилизирующих факторов и т. д.).

Точность обработки результатов анализа с помощью микропроцессорных устройств во многом зависит от адекватности формы ХП его математической модели.

Сложность физико — химических процессов, происходящих в анализаторе, не позволяет разработать идеальную модель ХП [5], так как теоретическое обоснование формы профиля ХП в виде симметричной кривой Гаусса в большинстве случаев не обеспечивает адекватности модели и реального пика. В связи с этим к настоящему времени разработано большое количество аналитических выражений, описывающих формы реально полученных ХП.

При разработке некоторых моделей использовалась теория процессов в анализаторе [4, 5], в других — модели получали эмпирическим путем подбора кривых по экспериментальным данным. Обычно модели проверялись на ХП одного вещества или небольшой группы анализируемых веществ. Универсальная модель ХП должна удовлетворять следующим требованиям:

высокая точность при описании ХП любой формы;

линейность относительно подбираемых параметров с целью упрощения расчета модели;

возможность управления режимом анализатора по оценке параметров модели, для чего параметры должны нести смысловую нагрузку с точки зрения процессов, происходящих в анализаторе;

представление интеграла от моделируемой функции ХП в пределах от — до +, который определяет площадь ХП в табличном виде.

Анализ известных аналитических моделей ХП показывает, что ни одна из них не удовлетворяет всем перечисленным требованиям. Наиболее полно поставленным условиям соответствует би — Гауссиан, однако точность описания с его помощью задних фронтов ХП, имеющих затянутые хвосты, невысока [2].

Так, например, аппроксимация хроматографических пиков воды, ацетона, хлороформа и нитрометана би — Гауссианом, изображенным на рис. 2, имеет погрешность аппроксимации 25%.

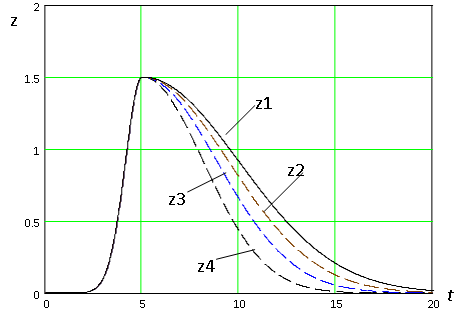
Рис. 2. Аппроксимация хроматографических пиков би — Гауссианом:

z1(t) — пик ацетона, z2(t) — пик воды, z3(t) — пик хлороформа,.

z4(t) — пик нитрометана.

хроматограмма гаусс пик аппроксимация Создание математической модели ХП, удовлетворяющей перечисленным выше требованиям, возможно на основе подхода, сущность которого заключается в том, что недостаток теоретических сведений о процессе в анализаторе компенсируется статистической информацией об его реализациях на хроматограмме.

Разработанная модель содержит две составляющие, одна из которых является результатом аналитических выводов из теории анализа, полученных при упомянутых выше ограничениях и допущениях, а другая, компенсирующая эти ограничения, является результатом статистического анализа большого числа форм ХП [5, 6].

Модель в этом случае представляется в виде суммы симметричной Гауссовой и некоторой функции (рис. 3).

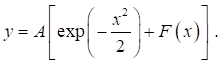
Статистический анализ большого числа несимметричных пиков с различной степенью асимметрии показал подобие функции F (x) для большинства анализируемых пиков. Наилучшим аналитическим приближением для такого типа кривых, существующих на полуоси (0,), является экспоненциально — степенной полином без свободного члена [2]:

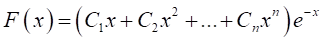
(2).

где C1 — Сn — коэффициенты полинома, зависящие от величины несимметрии аналитического пика.

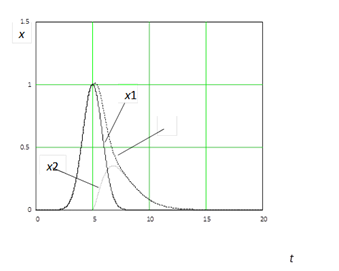
Рис. 3. Синтез математической модели несимметричного АП с помощью двух функций: x1(t) — Гауссова функция, x2(t) — экспоненциально — степенная функция, z (t) — модель ХП.

Как показала практика, для аппроксимации ХП достаточно всего трех членов полинома (2), в результате чего математическая модель несимметричных пиков записывается в виде.

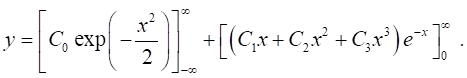
(3).

С помощью (3), основу (ядро) которого составляет функция Гаусса, можно с высокой точностью аппроксимировать ХП любой формы. Для симметричных пиков коэффициенты C1 — С3 равны нулю, а коэффициент С0 равен амплитуде пика. Для несимметричных пиков смысл коэффициента С0 остается прежним, а величины C1 — С3 зависят от степени асимметрии: для более асимметричных пиков возрастает вес коэффициента, имеющего больший порядковый номер.

Некоторые реальные и «синтетические» ХП, рассчитанные по выражению (3), коэффициенты которых C1 — С3 подбирались методом наименьших квадратов, для анализируемых веществ, принадлежащих к разным классам, показаны на рис. 4.

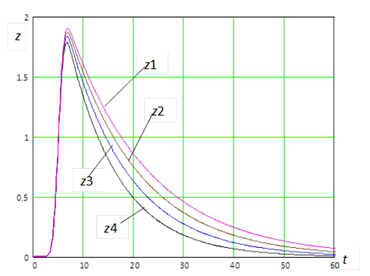
Рис. 4. Аппроксимация хроматографических пиков различных веществ математической моделью (2.35). z1(t) — пик воды, z2(t) — пик ацетона, z3(t) — пик хлороформа, z4(t) — пик нитрометана

Анализ экспериментальных данных показал, что максимальная погрешность аппроксимации не превышает 15% для всех анализируемых веществ, причем большие отклонения приходятся на самую нижнюю часть пика, доля площади которой в его общей площади весьма мала. В связи с этим отличие площади реального ХП от расчетного — незначительно (не более 2…3%). Это подтверждает адекватность выбранной модели и профиля ХП. Достоинством модели (3) является возможность аналитического определения площади пика, поскольку все интегралы этого выражения — табличные:

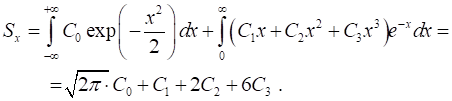
(4).

При переходе от записи (3) и (4) в относительных единицах к абсолютным площадь пика получается равной.

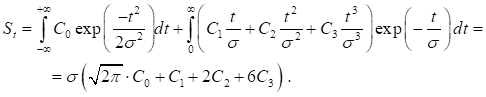
(5).

где — среднеквадратичная ширина переднего фронта ХП;

t — текущее (реальное) время.

Как видно из выражений (4) и (5), площадь пика довольно просто вычисляется через коэффициенты C1 — С3 .

Библиографический перечень

• 1. Гольберт К. А., Вигдергауз М. С. Курс газовой хроматографии. — М.:Химия, 1974. — 375с.
• 2. Ланге П. К., Шафранский И. В. Математическое описание несимметричных хроматографических пиков //Автоматизация и контрольно — измерительные приборы. — 1975. -№ 6. — С.13−16.
• 3. Grushka Е. Investigation of exponentially modifying Gauss peaks in chromatography // Аnal. Chem. — 1972. — № 11.
• 4. Bjuz Т.S., de Klerk К. Approximation non — symmetric chromatographic functions with byGaussian // Аnal. Chem. — 1972. — № 7.
• 5. Grubner O. Interpretation of non — symmetric curves in chromatography // Аnal. Chem. — 1971. — № 14.
• 6. Ланге П. К., Горбков А. Г. Построение математической модели хроматографического пика при аддитивности влияния процессов диффузии и сорбции //Сб. Успехи газовой хроматографии. Вып. 6. Казань. 1982. — с. 233−239.