Расчёт на прочность гофрированной тонкой пластины на упругом основании обратным методом

Аннотация

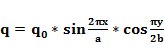
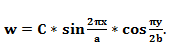
В работе рассматривается прямоугольная пластина, подкреплённая рёбрами жёсткости в двух взаимно перпендикулярных направлениях. Пластина опирается на упругое основание и нагружена распределённой нагрузкой по следующему закону. Задача решается обратным методом. Функция прогибов пластины задаются в виде: За расчётную схему принимается шарнирно опёртая ортотропная пластина на упругом Винклеровском основании. Исследуется напряженное состояние и проводится расчет на грузоподъемность для различных параметров пластины и основания. Расчёты показали, что грузоподъёмность волнистой пластины выше по сравнению с грузоподъёмностью плоской пластины.

Ключевые слова: гофрированная, пластина, упругое основание, обратный метод, тонкая, ортонормированная, изгиб, грузоподъёмность, прочность.

перпендикулярный прямоугольный пластина винклеровский Пластина на упругом основании является широко распространённой моделью конструктивных элементов объектов строительства, машиностроения, приборостроения, авиастроения, судостроения и т. д.

Аналитические решения для пластин являются альтернативными по отношению к решениям, полученным численными методами, если для расчетов ответственных объектов требуется подтверждение достоверности полученных результатов[1−4].

Проводилось исследование напряженного состояния и расчет на грузоподъемность для различных параметров пластины и основания. Выбор модели основания Винклера обусловлен тем, что, винклеровская модель математически проста и дает достаточно хорошие результаты.

Рис 1. Волнистая пластина на упругом основании. b — ширина пластины; a — длина пластины; fвысота волны пластины; l — длина волны пластины.

За расчётную схему принимается ортотропная шарнирно опёртая пластина, имеющая различные цилиндрические жёсткости в двух взаимно перпендикулярных направлениях, зависящих от жёсткости подкрепляющих рёбер.

Дифференциальное уравнение изгиба ортотропной пластины на упругом основании в этом случае имеет вид[7−11]:

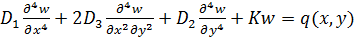
(1).

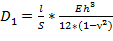
где (2).

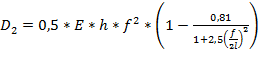
(3).

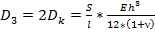
(4).

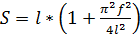
(5).

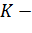
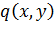
коэффициент постели, — распределённая нагрузка, wпрогиб пластины, hтолщина пластины, E-модуль упругости при растяжении, — коэффициент Пуассона, fамплитуда волны, — длина волны.

Нагрузка, действующая на пластину, распределена по закону:

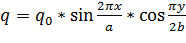
(6).

Функция прогибов пластины задаются в следующем виде:

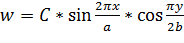
(7).

Постояннаяопределяется из уравнения (1):

.

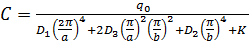
Максимальные нормальные напряжения определяются по формулам:

=.

= .

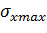
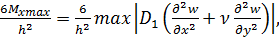
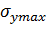
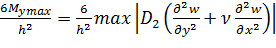
Из условия прочности по нормальным напряжениям определяем Таблица 1 — Грузоподъемность пластины в зависимости от высоты волны.

Высота волны f, м.	Длина волны l, м.	Максимальное нормальное напряжение.	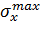Предельно допускаемая нагрузка, МПа.	Максимальное нормальное напряжение.	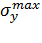Предельно допускаемая нагрузка, МПа.
0,01.	0,05.	0,83.	192,77.	10,24.	15,63.
0,0125.		0,797.	200,75.	16,74.	9,56.
0,015.		0,749.	213,6.	25,59.	6,25.
0,018.		0,69.	231,88.	39,49.	4,05.
0,02.		0,66.	242,4.	50,7.	3,16.

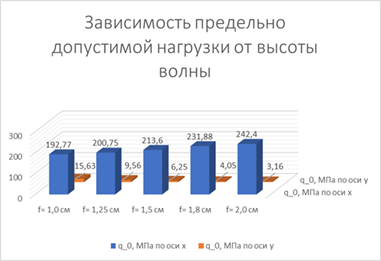
Диаграмма 1 — f — высота волны, — Предельно допустимая нагрузка, МПа.

Как видно из результатов расчетов, чем больше высота волны, тем больше предельно допускаемая нагрузка по оси х и меньше по оси у.

Таблица 2 — Грузоподъемность пластины в зависимости от длины волны.

Длина волны l, м.	Высота волны f, м.	Максимальное нормальное напряжение.	Предельно допускаемая нагрузка, МПа.	Максимальное нормальное напряжение.	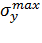Предельно допускаемая нагрузка, МПа.
0,04.	0,01.	0,857.	186,7.	10,7.	14,95.
0,05.		0,83.	192,77.	10,24.	15,63.
0,06.		0,857.	186,7.	9,9.	16,2.
0,07.		0,874.	183,07.	9,75.	16,4.
0,08.		0,88.	181,8.	9,65.	16,58.

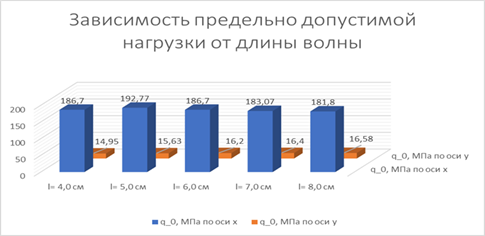
Диаграмма 2 — l — длина волны, — Предельно допустимая нагрузка, МПа.

Вывод: чем больше длина волны пластины, тем меньше предельно допускаемая нагрузка по оси х и больше по оси у.

Таблица 3 — Грузоподъемность пластины в зависимости от коэффициента постели упругого основания.

Коэффициент постели основания К, Мпа/м.	Длина волны l, м.	Высота волны f, м.	Максимальное нормальное напряжение.	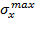Предельно допустимая нагрузка, МПа.	Максимальное нормальное напряжение.	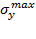Предельно допустимая нагрузка, МПа.
100 (песок).	0,05.	0,01.	3,3.	48,5.	40,95.	3,9.
200 (грунт песчано-глинистый, уплотненный).			1,66.	96,38.	20,475.	7,8.
400 (известняк).			0,83.	192,77.	10,24.	15,63.
600 (бутовая кладка).			0,55.	290,9.	6,8.	23,53.
800 (бетон).			0,42.	380,95.	5,1.	31,37.

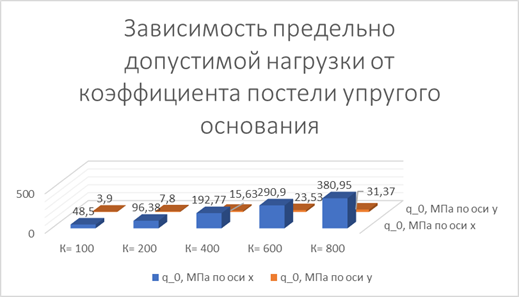
Диаграмма 3 — К — коэффициент постели, — Предельно допустимая нагрузка, МПа.

Вывод: из расчетов видно, что между коэффициентом жесткости упругого основания и предельно допустимой нагрузкой по оси х и у, прямо пропорциональная зависимость.

Входе исследования был проведен сравнительный анализ предельно допустимой нагрузки для гофрированной пластинки и прямоугольной плоской пластины. Результаты расчетов показали, что выгоднее использовать гофрированную пластину.

Таблица 4 — Результаты расчетов прямой прямоугольной и гофрированной пластин.

	Длина волны l, м.	Высота волны f, м.	Максимальное нормальное напряжение.	Предельно допустимая нагрузка, МПа (расчёт по).	Максимальное нормальное напряжение.	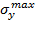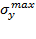Предельно допустимая нагрузка, МПа (расчёт по).
Плоская пластина.	0,05.	0,01.	0,177.	903,95.		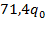2,24.
Гофрированная пластина.			0,83.	192,77.	10,24.	15,63.

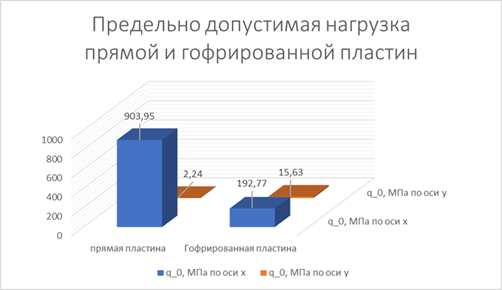
Диаграмма 4. — Предельно допустимая нагрузка (МПа).

Вывод Исследование показало, что грузоподъёмность, гофрированной пластины выше, чем прямоугольной. Несмотря на то, что предельно допустимая нагрузка по оси х намного больше у прямой пластины, предельно допустимая нагрузка по оси у в 6,9 раз в прямой пластине меньше, чем в гофрированной пластине.

Исследование показало, что напряженное состояние и грузоподъемность гофрированной пластины на упругом основании во многом зависит от геометрических параметров пластины и от жесткости основания, на которое опирается сама пластина. Данный метод позволяет исследовать влияние параметров пластины, рёбер и характеристик упругого основания на прочность волнистой пластины на упругом основании при изгибе и востребован при расчёте элементов инженерных конструкций[12−14].

• 1. Кадомцева Е. Э., Моргун Л. В. Учёт влияния отличия модулей упругости на сжатие и растяжение при расчёте на прочность армированных балок с заполнителем из фибропенобетона. // Инженерный вестник Дона, 2013, № 2 URL: ivdon.ru/magazine/archive/n2y2013/1655/.
• 1. 2. Кадомцева Е. Э., Бескопыльный А. Н. Расчёт на прочность армированных балок с заполнителем из бимодульного материала с использованием различных теорий прочности. // Инженерный вестник Дона, 2013, № 4 URL: ivdon.ru/magazine/archive/n4y2013/2125/.
• 2. 3. Матвеев С. А., Мартынов Е. А., Литвинов Н. Н. Расчёт армированной дорожной одежды как многослойной плиты на упругом основании. // Вестник Сибирской государственной автомобильно-дорожной академии. Сер.: Механика. 2015. Вып.4(45)c. 72−76.
• 3. 4. Большаков А. А. Прямоугольная пластина, упруго опертая по контуру // Интернет-вестник ВолгГАСУ. Сер.: Политематическая. 2011. Вып. 4 (19). URL: vestnik.vgasu.ru
• 4. Belen’kii D.M., Beskopyl’nyi A.N., Vernezi N.L., Shamraev L.G. New approach to the strength analysis of awelded butt joint. Industrial Laboratory. 1996. V., C. 62. № 8. pp. 517−520.
• 5. Беленький Д. М., Бескопыльный А. Н. Измерение вектора механических свойств материала деталей машин. Вестник машиностроения. 1997. № 8. С. 44.
• 6. 7. Кадомцева Е. Э., Бескопыльный А. Н., Бердник Я. А. Расчёт на жёсткость пластины, подкреплённой рёбрами, на упругом основании методом Бубнова-Галёркина. Инженерный вестник Дона, 2016, № 3 URL: ivdon.ru/magazine/archive/n3y2016/3699/.
• 7. Филин А. П. Прикладная механика твёрдого деформируемого тела. Т.1. — М. изд-во" Наука", Гл. ред. физ.-мат. литературы, 1981. -832 с.
• 8. 9. Симвулиди И. А. Расчет инженерных конструкций на упругом основании. -М. Высшая школа 1987. — 576 с.
• 9. Прочность, устойчивость, колебания. Справочник в трёх томах. Под общей редакцией Биргер И. А. и Пановко Я. Г. Т.2. — М., изд-во «Машиностроение», 1988. с. 464.
• 10. Мышкис А. Д. Прикладная математика для инженеров. Специальные курсы. — М. изд-во «Физматлит», МАИК «Наука/Интерпериодика», 2007.-687 с.
• 11. Бенерджи П., Баттерфилд Р. Метод граничных элементов в прикладных науках: Пер. с англ.-М.: Мир, 1984.-494 с.
• 12. Shukla S.K. Shallow foundations in geosynthetics and their applications. -Editor Thomas Telford, London. 2002. pp. 123−163
• 13. Yin J.H. Comparative modeling study on reinforced beam on elastic foundation. In Journal of Geotechnical and Geoenvironmental Engineering, ASCE, Vol.126, No.3., pp.265−271.
• 14. KadomcevaE.E., Morgun L.V. Inћenernyj vestnik Dona (Rus), 2013, № 2 URL: ivdon.ru/magazine/archive/n2y2013/1655/.
• 15. Kadomceva E.E., Beskopyl’nyj A.N. Inћenernyj vestnik Dona (Rus), 2013, № 4 URL: ivdon.ru/magazine/archive/n4y2013/2125/.
• 16. Matveev S.A., Martynov E.A., Litvinov N.N. Vestnik Sibirskoj gosudarstvennoj avtomobil’no-dorozhnoj akademii. Ser.: Mehanika. 2015. Vyp.4 (45) 72.76 p.
• 17. Bol’shakov A.A. Internet. vestnik VolgGASU. Ser.: Politematicheskaja. 2011. Vyp. 4 (19). URL.vestnik.vgasu.ru
• 18. Belen’kii D.M., Beskopyl’nyi A.N., Vernezi N.L., Shamraev L.G. Industrial Laboratory. 1996. V. 62. № 8. pp. 517.520.
• 19. Belen’kij D.M., Beskopyl’nyj A.N. Vestnik mashinostroenija. 1997. № 8. p. 44.
• 20. Kadomceva E.Je., Beskopyl’nyj A.N., Berdnik Ja.A. Inћenernyj vestnik Dona (Rus), 2016, № 3 URL: ivdon.ru/magazine/archive/n3y2016/3699/.
• 21. Filin A.P. Prikladnaja mehanika tvjordogo deformiruemogo tela. [Applied mechanics of a rigid deformable body.] V.1. M. izd. vo" Nauka", Gl. red.fiz.mat. literatury, 1981. 832 p.
• 22. Simvulidi I.A. Raschet inzhenernyh konstrukcij nauprugom osnovanii. [Calculation of engineering structures on an elastic foundation] M. Vysshajashkola. 1987. 576 p.
• 23. Prochnost', ustojchivost', kolebanija. Spravochnik v trjohtomah. Pod obshhejredakciej Birger I.A. i PanovkoJa.G. [Strength, stability, vibrations. Reference book in three volumes. Under the general editorship Birger IA and PanovkoYa.G.] V.2. M., izd. vo «Mashinostroenie», 1988. p.464.
• 24. Myshkis A.D. Prikladnaja matematika dlja inzhenerov. Special’nye kursy. [Applied mathematics for engineers. Special courses.] M. izd. vo «Fizmatlit», MAIK «Nauka. Interperiodika», 2007. 687 p.
• 25. Benerdzhi P., Batterfild R. Metod granichnyhj elementov v prikladnyh naukah.: Per. s ang. [Method of boundary elements in applied sciences: Trans. with eng.]M.: Mir, 1984. 494 p.
• 26. Shukla S.K. Editor Thomas Telford, London. 2002. pp. 123−163.
• 27. Yin J.H. In Journal of Geotechnical and Geoenvironmental Engineering, ASCE, Vol.126, No.3., pp.265−271.