О краевой задаче теории упругости в полярной системе координат

Аннотация

В статье изложена постановка краевой задачи деформируемого твердого тела в полярной системе координат. Задача приведена к особому интегральному уравнению, решение которого позволяет определить местные напряжения на линии сопряжения возле их концентрации.

Ключевые слова: концентратор напряжений, упругое тело, местные напряжения, краевая задача, интегральное уравнение.

В современных машинах широко применяются осесимметрично нагруженные детали сложной формы, ослабленные различными концентраторами напряжений, в близи границ которых возникают значительные местные напряжения, поэтому возникает необходимость в отыскании решения краевой задачи в полярной системе координат [1, 2].

С точки зрения расчетной схемы любую деталь можно представить как упругое тело единичной толщины произвольной формы, подвергающееся воздействию внешних нагрузок Р_n и находящееся в состоянии равновесия (рис. 1 а).

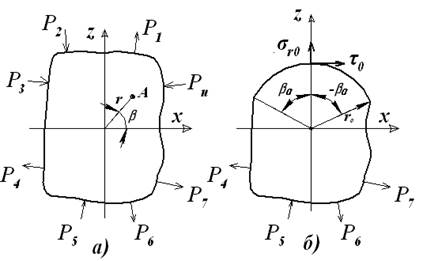
Рис. 1. Плоское упругое тело: а) расчетная схема; б) элемент тела с круговым сечением

Пусть координатами точки А будут полярный радиус r, отсчитываемый от центра тяжести, и угол в.

Для исследования напряженно-деформированного состояния воспользуемся уравнениями Ламе, описывающими равновесие бесконечно малого элемента сплошной среды в перемещениях без учета массовых сил, которые в полярной системе в условиях плоского деформированного состояния примут вид [3]:

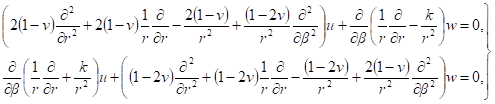
(1).

где н — коэффициент Пуассона; u и w — перемещения точек в полярной системе координа в, r; .

Введем новую переменную, с=const, тогда систему (1) можно привести к уравнениям с постоянными коэффициентами [1, 3].

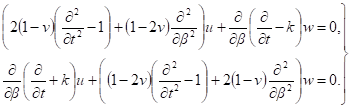
(2).

Решение системы (2) ищем в виде интегрального преобразования Фурье [4].

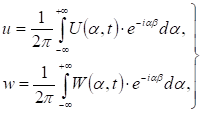
(3).

где б — произвольное вещественное число.

После подстановки (3) в (2) имеем систему уравнений:

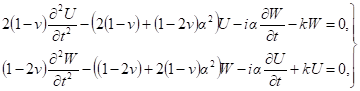
решение которой может быть представлено в виде [1]:

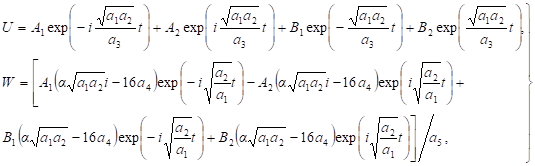
(4).

где A_n, B_n (n=1, 2) — постоянные, подлежащие определению из краевых условий;

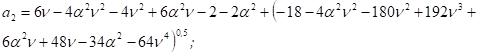
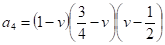
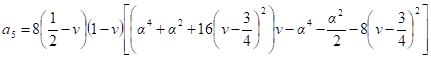
Уравнения (4) можно привести к эквивалентным смешанным гиперболическим и тригонометрическим функциям [3].

Подставляя (4) в (3) определяем перемещения u и w. По формулам Коши находим деформации.

;

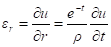
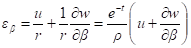
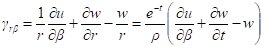
а по закону Гука — напряжения:

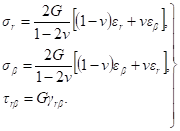
Задаемся следующими краевыми условиями:

1) Из условий симметрии, без жесткого перемещения тела и при отсутствии полости в начале координат.

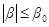
где t₀-му соответствует радиус сектора r₀, с углом полураствора в₀ (рис. 1 б).

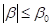
Если у_r0 и ф₀ рассматривать в качестве местных напряжений, то они в основном должны зависеть от перемещений на дуге сектора и мало зависеть от r₀, поэтому необходимо устремить его к бесконечности. Здесь координаты в₀ и r₀ определяют границы концентратора напряжений. Решить задачу удается только численными методами, однако при приходим к выражению [1, 4−7]:

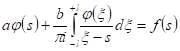
(5).

где а, b — постоянные, зависящие от упругих свойств материала; s — дуговая абсцисса линии интегрирования (сопряжения), соответствующая углу в₀; l — полуширина линии сопряжения;

Индекс 1 означает местный характер напряженно-деформированного состояния.

Частные решения интегрального уравнения (5) представлены в [4−10].

Итак, интегральное уравнение (5) может быть использовано для решения краевых задач в полярных координатах при определении местных напряжений на какой-либо дуге интегрирования, в качестве которой может служить как внешний контур тела, так и какая-либо дуговая линия сопряжения возле концентратора напряжений внутри плоского тела.

полярный уравнение напряжение концентрация.

• 1. Дородов П. В. Комплексный метод расчета и оптимального проектирования деталей машин с концентраторами напряжений: монография. — Ижевск: ФГБОУ ВПО Ижевская ГСХА, 2014. 316 с.
• 2. Ерохин М. Н., Дородов П. В. Метод оптимального проектирования деталей в зоне контакта // Вестник Федерального государственного образовательного учреждения высшего профессионального образования «Московский государственный агроинженерный университет им. В.П. Горячкина». 2014. № 3. С. 5−8.
• 3. Mixed boundary value problems of potential theory and their applications in engineering / by V.I. Fabrikant. Boston: Kluwer Academic Publishers, c1991. 451 p.
• 4. Александров В. М., Чебаков М. И.

  Введение

  в механику контактных взаимодействий. — Ростов-на-Дону: Изд-во ООО «ЦВВР», 2007. 114 с.

• 5. Мусхелишвили Н. И. Сингулярные интегральные уравнения. — М.: Изд-во «Наука», 1968. 512 с.
• 6. Trjitzinsky W.J. Singular integral equations with Cauchy kernels // Trans. Amer. Math. Soc.- 1946. -V.60. № 2. рр.167−214.
• 7. Дородов П. В. Приведение краевой задачи для плоского упругого тела к одному особому интегральному уравнению // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета, 2012, № 80. С. 1−10 URL: ej.kubagro.ru/2012/06/pdf/14.pdf.
• 8. Дородов П. В. Исследование напряжений на линии сопряжения ступенчатой пластины // Инженерный вестник Дона, 2013,№ 2. URL: ivdon.ru/ru/magazine/archive/n2y2013/1636.
• 9. Дородов П. В., Кулагин А. В. Исследование напряжений в окрестности плоского горизонтального выреза // Инженерный вестник Дона, 2012, № 2 URL: ivdon.ru/ru/magazine/archive/n2y2012/813.
• 10. Ерохин М. Н., Дородов П. В. Уточненный расчет и определение коэффициента концентрации напряжений в деталях машин, ослабленных боковыми вырезами // Международный технико-экономический журнал. 2014. № 4. С. 77−83.