Принцип Гюйгенса — Френеля

Геометрическая оптика основана на принципе прямолинейности распространения света в однородной среде. Кроме того, принималось как самоочевидное то, что световой пучок можно всегда разбить на любое число бесконечно тонких лучей и рассматривать распространение каждого из этих лучей отдельно.

При рассмотрении явлении интерференции мы также все время пользуемся представлением бесконечно тонких световых лучей, прямолинейно распространяющихся в однородной среде. Уточнение по сравнению с геометрической оптикой состояло лишь в том, что эти лучи рассматривались как направление распространения световых колебаний.

Однако ряд фактов показывает необходимость дальнейшего уточнения наших представлений о процессе распространения световых колебаний. Необходимость такого уточнения возникает при первой же, самой простой попытке получить на опыте достаточно узкий световой луч, т. е. при попытке получить экспериментально те практически бесконечно узкие лучи, представлением о которых мы так широко пользовались ранее.

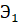
Проще всего получить узкий световой луч, взяв достаточно маленький источник света S, поместив на некотором расстоянии от него непрозрачный экран Э с небольшим отверстием. Диаметр светового пятна ab ,получающегося на экране, помещенном за экраном Э, будет характеризовать ширину получающегося светового пучка (рис. 1.1).

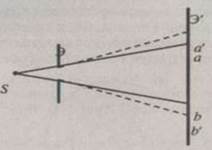
рис. 1.1.

Согласно идеям геометрической оптики следует ожидать, что чем меньше будет диаметр отверстия в экране Э, тем меньше будет диаметр светлого пятна на экране или, иными словами, тем уже будет световой луч. При достаточно малых размерах источника S, делая отверстие в экране сколь угодно малым, мы должны получить сколь угодно малое пятно на экране или сколь угодно узкий луч.

Опыт, однако, дает совершенно неожиданный результат: начиная с определенного размера отверстия, дальнейшее его уменьшение вызывает не уменьшение пятна на экране, а увеличение. При этом пятно уже теряет свою резкость, становится расплывчатым и освещенным неравномерно: на нем появляется ряд колец, заполняющих область, значительно более широкую, чем это следует из геометрических соображений. Расширению пятна соответствует, конечно, и расширение светового луча. Таким образом, попытка получить столь угодно узкий луч света терпит неудачу.

Описанное явление является одним из проявлений дифракции, точное определение которой мы дадим несколько позже. В нашем опыте дифракция проявляется в том, что световые лучи отклоняются от прямолинейного пути распространения. Оказывается, что это свойство присуще всем волнам без исключения независимо от их природы.

Для объяснения явлений, аналогичных только что рассмотренному, создатель волновой теории света голландский физик Х. Гюйгенс выдвинул принцип. Разберемся в сущности этого принципа. Гюйгенс рассматривал распределение световых волн как последовательное возмущение точек эфира, в котором распространяется свет. Каждая точка волнового фронта (т.е. геометрическое место точек в пространстве, до которых дошел процесс распространения колебаний, и колеблющихся поэтому в одинаковой фазе) является самостоятельным источником вторичных волн, распространяющихся со скоростью света.

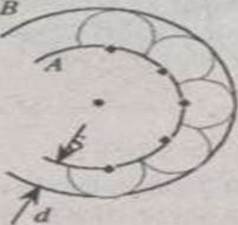
рис. 1.2.

Рассмотрим распространение света в изотропной среде, в которой скорость света по всем направлениям одинакова. Пусть в некоторый момент времени фронт волны находится в положении A (рис. 1.2). Все точки поверхности A начинают одновременно посылать колебания со скоростью c (эти вторичные волны представлены на рисунке малыми окружностями).

Как показал Кирхгоф, интенсивность этих вторичных волн будет наибольшей в направлении нормали к волновой поверхности, т. е. излучение вторичных источников, «вспыхивающих» на фронте волны, носит резко направленный характер. В результате через время t колебания распространяться на расстояние.

d=ct ,.

что, очевидно, будет соответствовать перемещению всего фронта в положение В. Фронт волны В по определению, должен проходить через все точки пространства, колеблющихся в одной фазе; следовательно, он касается всех сфер радиуса d, представляющих вторичные волновые поверхности через время t.

Итак, принцип Гюйгенса может быть сформулирован следующим образом.

• 1. Каждая точка пространства, до которой дошел колебательный процесс (каждая точка фронта волны), является источником вторичных сферических волн.
• 2. Волновой фронт, образованный вторичными волнами, есть поверхность, огибающая поверхности вторичных волн.
• 3. Световые лучи расходятся по радиусам от точечного источника.
• 4. В изотропной среде световые лучи являются нормалями к волновой поверхности.

Рис. 1.3.

Пользуясь принципом Гюйгенса, можно вывести законы отражения и преломления света. Пусть на зеркало MN падает плоская световая волна (рис. 1.3). В некоторый момент волновая поверхность АВ касается зеркала в точке А. Здесь возникают вторичные колебания, распространяющиеся со скоростью света с. Время запаздывания t, за которое колебания достигнут зеркала от точки В, равно t=BC/c. За это время вторичные колебания, распространяющиеся с той же скоростью с, достигнут сферы с радиусом AD = ВС. Можно показать, что все точки в плоскости CD, перпендикулярной к плоскости чертежа, обладают одной фазой и, следовательно, плоскость CD является фронтом отраженной волны. Из полученного геометрического построения отраженной волновой поверхности CD следует закон отражения света: углы падающего луча AT и отраженного AR с нормалью An равны друг другу.

Рассмотрим две среды, границу раздела MN между которыми для простоты будем считать плоской (рис. 1.4). Пусть на поверхность раздела падает плоская волна AB. Скорость волны в первой среде обозначим через, а во второй среде — через. Колебания в точках А и В находятся в одной фазе. В тот момент, когда фронт волны АВ касается границы раздела MN, от точки А во второй среде начинают распространяться вторичные колебания со скоростью. В это же время колебания от точки В распространяются со скоростью. Расстояние ВС в первой среде колебания проходят за время. За.

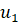
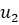
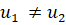
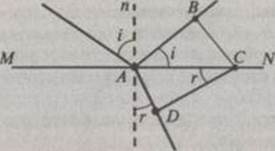
рис. 1.4.

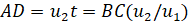
это время вторичные колебания из точки А достигнут сферы радиуса. При этом все точки сферы будут иметь фазу, одинаковую с фазой в точке С, и, следовательно, волновой поверхностью во второй среде будет плоскость CD, перпендикулярная плоскости чертежа. Произошел поворот фронта волны. Из прямоугольных треугольников АВС и ACD найдем.

.

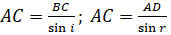
Тогда.

.

откуда.

.

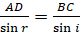
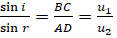
Таким образом, мы получили уже известный нам закон преломления света.

В разнообразных случаях волновая теория Гюйгенса приводит к тем законам, что и геометрическая оптика. Разница заключается пока только в том, что в геометрической оптике законы отражения и преломления рассматривались как экспериментальные данные, а волновая теория по существу дает нам объяснение этих законов, основанное на представлении о природе света. Преимущество волновой теории этим, однако, не ограничивается. Как уже говорилось, эта теория дает возможность объяснения и таких фактов, которые не укладываются и рамки геометрической оптики (дифракция). Такие эффекты возникают при экранировании части волнового фронта или при встрече волнового фронта световой волны с другими резкими неоднородностями.

Совокупность огромного количества опытных данных по распространению света позволяет определить явление дифракции следующим образом: дифракцией называется совокупность явлений, наблюдаемых при распространении волнового процесса в среде с резкими неоднородностями и связанных с отклонениями от законов геометрии.

Дифракция, в частности, приводит к огибанию волнами препятствий и проникновению волн в область геометрической тени. Огибание препятствий звуковыми волнами (т.е. дифракция звуковых волн) наблюдается постоянно в обыденной жизни (мы слышим звуки от источника, находящегося за «углом»). Для наблюдения дифракции световых волн необходимо создание специальных условий. Это вызвано тем, что появление, четкость и резкость дифракционной картины сильно зависят от соотношения размеров препятствий и длины волны. При длине волны, соизмеримой с размерами препятствия (что обычно имеет место для звуковых волн), дифракция выражена очень сильно. В случае, если длина волны значительно меньше размеров препятствия, как это имеет место для света, дифракция выражена слабо и обнаруживается с трудом.

Явление дифракции волн может быть качественно объяснено с помощью принципа Гюйгенса. Однако никаких количественных оценок принцип Гюйгенса не дает. Это означает, что принцип Гюйгенса не дает никаких указаний об амплитуде, а следовательно, и об интенсивности вторичных волн, распространяющихся в различных направлениях. Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства.

Принцип Гюйгенса в его же формулировке имел характер геометрического правила, согласно которому результат действия вторичных волн может быть найден построением поверхности, огибающей эти волны. Френель, заимствовав из принципа Гюйгенса представление о вторичных волнах, применил к ним законы интерференции. Согласно Френелю, правило построения огибающей поверхности должно быть запенено расчетом взаимной интерференции вторичных волн.

С помощью усовершенствованного им принципа Френелю удалось дать удовлетворительное объяснение ряда дифракционных явлений, а также устранить одно из основных затруднений волновой теории света — показать, как согласуются волновая природа с наблюдающимся на опыте прямолинейным распространением света.

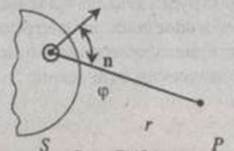
рис. 1.5.

Пусть S на рис. 1.5 представляет собой одну из волновых поверхностей света, распространяющегося от некоторого источника. Амплитуда светового колебания в некоторой точке Р, лежащей перед этой поверхностью, может быть найдена согласно Френелю следующим образом. Каждый элемент поверхности dS служит источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента dS. Амплитуда сферической волны убывает с расстоянием по закону 1/r. Следовательно, от каждого элементарного участка dS волновой поверхности S в точку Р приходит колебание.

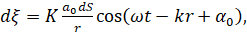
(1.1).

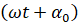
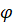
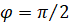
где — фаза колебания в месте расположения волновой поверхности S; k — волновое число; r — расстояние от элемента поверхности dS до точки P; о— значение колеблющейся величины (в нашем случае светового вектора Е) в точке Р в данный момент времени. Величина определяется амплитудой светового колебания в том месте, где находится элемент поверхности dS. Коэффициент пропорциональности К Френель считал убывающим при увеличении угла между нормалью n к dS и направлением от dS к точке Р (при К = 0).

Результирующее колебание в точке Р представляет собой суперпозицию колебаний (1.1). взятых по всей волновой поверхности S:

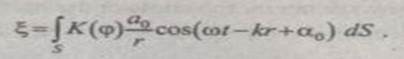
(1.2).

Формула (1.2) представляет собой аналитическое выражение объединенного принципа Гюйгенса—Френеля.

Вычисление по формуле (1.2) представляет собой в общем случае чрезвычайно трудную задачу. Однако, как показал Френель, в случаях, отличающихся симметрией, нахождение амплитуды результирующего колебания может быть осуществлено простым алгебраическим или геометрическим суммированием.

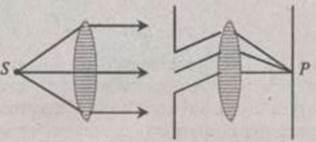
Рис. 1.6.

Различают два случая дифракции. Если источник света и точка наблюдения Р расположены относительно препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку Р, образуют практически параллельные лучи, то говорят о дифракции Фраунгофера или дифракции в параллельных лучах. В противном случае говорят о дифракции Френеля.

Дифракцию Фраунгофера можно наблюдать, поместив за источником света S и перед точкой наблюдения Р по линзе так. чтобы точки S н Р оказались в фокальных плоскостях соответствующих линз (рис. 1.6).