Эллиптические функции Якоби

Будем называть эллиптическими функциями Якоби три функции, определяемые формулами:

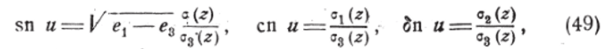
где ubzzzv

Пользуясь формулами (47) и (48), мы усматриваем, что это будут эллиптические функции: sn и имеет основные периоды 4ш У е_х—е₃, 2о)' V — 3; сп и имеет периоды 4со Уе_х —е₃, (2<�о 2<�о') Vе_х —е_г и.

?п и имеет периоды 2<�о У е_х— е₃, 4to' Уе_{—е₃.

Зная нули функций о (z) и a_k (г), мы можем написать нули и полюсы эллиптических функций Якоби в виде таблицы на стр. 292.

*) Под Vе—?₃ мы можем понимать любое из двух возможных его значений, гак как формулы (49) не изменяются при перемене знака у радикала Vei — e_s вследствие нечётности функции о и чётности функции о_л.

Очевидно, в основном параллелограме периодов лежат два простых нуля и два простых полюса каждой функции Якоби. Таким образом, это будут эллиптические функции второго порядка. Так как и — функция нечётная, a a_k — чётные,¹ то sn и — нечётная функция, сп и и Ьг и — функции чётные. Далее, sn0 = 0, сп0 = 1, $п0=1.

Не изменяя величины и, умножим шиш' на произвольное число к" тогда z умножится на ?, так как Ve_t—e_t разделится на к (е_{ и e_s однородны относительно о, о/ порядка — 2).

Отсюда, принимая во внимание свойства однородности функций а (г) и o_k(z) относительно z, о, <�о', мы выводим заключение: функции Якоби sntf, спн, дп и не изменяются, если умножить ш и о>' на произвольное число. Другими словами, эти функции нулевого измерения.

/ а/.

относительно со, со, т. е. зависят от и и отношения т = —.

' со Поэтому, если мы хотим явно выразить зависимость функций Якоби от периодов, то их следует обозначать через.

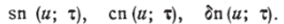
Из известных формул (z) — e_k = путём исключения функции $?> (z), получим два соотношения, связывающих три функции Якоби:

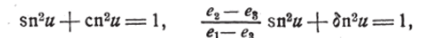
или, полагая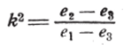

(к называется модулем наших функций), получим:

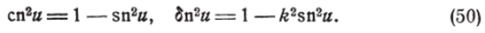
Пользуясь функциями Якоби (49), перепишем известное соотношение (43).

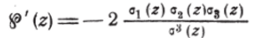
в виде:

С другой стороны, дифференцируя относительно и соотношение

найдём:

Сравнивая (52) и (51), получим:

Дифференцируя теперь тождества (50) и пользуясь (53), получим формулы производных для двух других функций Якоби:

(спи)' = — sntt&nH, ($п и)' = •— &²sn и спи. (54).

Чтобы получить дифференциальное уравнение для функции snw, возведём в квадрат соотношение (53) и воспользуемся формулами (50); тогда получим: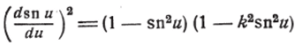

или, полагая x = snи, будем иметь:

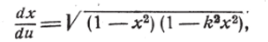
причём при и = 0 следует считать х = 0 и радикал, стоящий справа, равным единице, так как sn'(0) = l в силу (53).

Разделяя переменные и интегрируя, найдём: ₄

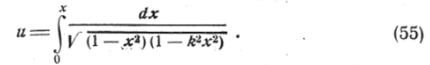
Отсюда мы видим, что функция sn и получается в результате обращения эллиптического интеграла первого рода в форме Лежандра.

Можно показать и наоборот, что, задавая произвольное комплексное число /г², отличное только от 0 и 1, получим в результате обращения интеграла (55) функцию Якоби sn". Это означает, что элементом построения для функций Якоби вместо т может служить число k. В дальнейшем мы подробно исследуем интеграл (55) с точки зрения конформного отображения для того частного случая, когда число k действите аьное и заключается между 0 и 1.

Мы увидим, что в этом случае один период будет действительным, а другой — чисто мнимым. Заметив, что при z = со, т. е. при и = в> V—е_я, функция сп и обращается в нуль, а значит sn и равна единице, поэтому

Интеграл, стоящий в правой части (56), выражает, следовательно, четвёртую часть периода функции sn и.