Классификация нормальных колебаний по форме и симметрии

Если при данном нормальном колебании происходит изменение длины связи, а углы меняются мало то такое колебание называется валентным (х).

Если при колебании изменяются углы между связями, а длины связей не меняются, такое колебание называется деформационным:

1. плоскостные (ножничные) [д]:

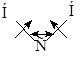
• 2. не плоскостные [р]:
• 3. веерные колебания [щ]
• 4. крутильные [с_t]
• 5. маятниковые [с_r]

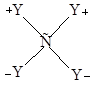
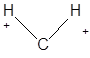
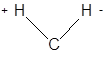
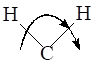
Если при данном колебании не происходит изменения симметрии равновесной конфигурации молекулы (не один из элементов симметрии не исчезает), то его относят к симметричным.

Если колебание сопровождается изменением симметрии равновесной конфигурации молекулы, то его относят к антисимметричным (А_S).

d — вырожденные колебания т. е. колебании с одинаковой частотой.

Рассмотрим нормальные колебания воды. Это трех атомная не линейная молекула. Её элементы симметрии: две у_v1,2 и С₂.=> точечная группа С_2v.

Для молекулы воды возможно: 3N — 6 => 3*3 — 6=3.

• 1. валентное симметричное;
• 2. деформационное симметричное;
• 3. валентное антисимметричное.

При последнем виде колебания пропадает у_v1 и С₂.

Для характеристики симметрии колебаний употребляются специальные обозначения в виде символов с различными индексами которые предложены Малликеном.

Символика Малликена

Не вырожденные колебания:

• а) симметричные относительно главной оси симметрии молекулы обозначается (А);
• б) антисимметричные относительно главной оси симметрии молекулы обозначается (В);

Дважды вырожденные обозначаются (Е);трижды вырожденные (F).

Индексом 1; 2 обозначают соответственно колебания различающиеся по отношению к плоскости у_v (1 — симметричные, 2 — антисимметричные) или по отношению к повороту вокруг оси симметрии отличной от главной: (1 — симметричные, 2 — антисимметричные).

1 или 2 штриха справа вверху обозначают колебания соответственно (1 штрих — симметричные, 2 штриха — антисимметричные) относительно плоскости отличной от у_v (например горизонтальная).

Индексами g и u от слов gerade и ungerade соответственно, помещенными внизу, обозначают симметричные колебания (g), и антисимметричные (u) относительно центра симметрии.

Предпочтение отдается индексам 1; 2 затем штрихом, а далее g и u.

В соответствии с этим колебания молекул воды обозначаются по символике Малликена.

• 1. А₁
• 2. А₁
• 3. В₁ (не симметрично С₂ но симметрична к у_v2).

Рассмотрим нормальные колебания молекулы СО ₂, трех атомной линейной молекулы.

Определяем элементы симметрии.

Точечная группа D_?h, число колебаний 4.

Деформационные колебания дважды вырожденные (Д_б).

Правила отбора в колебательных спектрах

Молекула поглощает оптическое излучение только тогда, когда происходит изменение её дипольного момента. В противном случае оптическое излучение не поглощается молекулой. Условия, определяющие возможность поглощения света молекулой, называются правилами отбора. Переходы, возможные по этим правилам, называются разрешенными, а невозможные — запрещенными.

Необходимо иметь в виду, что термин «запрещенный» относится к свободной молекуле. Условия свободной молекулы наиболее близко реализуются в разреженном газе. В действительности переходы, запрещенные в свободной молекуле, могут частично разрешаться по ряду причин, преимущественно обусловленных взаимодействием молекул, в иных средах.

Правила отбора связаны в первую очередь со свойствами симметрии данной системы. Особо важное значение имеют правила отбора для дипольного (имеется в виду электрический диполь) излучения, для которого разрешенным переходам соответствуют большие по сравнению с квадрупольным или магнитным излечениями вероятности (порядка 106 раз).

Для каждой точечной группы симметрии легко найти структуру представления, преобразовав компоненты дипольного момента или поляризуемости. Иными словами, можно указать, к каким типам симметрии относятся соответствующие компоненты дипольного момента или тензора поляризуемости. Эти типы симметрии уже рассчитаны и сведены в таблицы характеров точечных групп симметрии.

Таким образом, оказывается, что переход в молекуле будет разрешен, если симметрия составляющих p и б совпадает с симметрией другого колебательного состояния, переход в которое мы рассматриваем. Следовательно, можно сформулировать правило отбора при ИК-поглощении или КР для случая основных частот, получающихся при переходе из нулевого колебательного состояния, которое является всегда полно-симметричным, в состояния, в которых возбуждено одно из нормальных колебаний. Итак, разрешены такие переходы, для которых симметрия рассматриваемой составляющей дипольного момента или тензора поляризуемости совпадает с симметрией данного нормального колебания.

Для молекул, имеющих центр симметрии, составляющие дипольного момента всегда принадлежат к нечетным типам симметрии, а составляющие тензора поляризуемости — к четным. В результате нечетные колебания, активные в ИК-спектре, неактивны в КР, а четные колебания, активные в спектре КР, неактивны в ИК-поглощении. Таким образом, имеет место альтернативный запрет.

Из этого можно получить правила отбора следующего вида:

ИК — g > u.

RH — g > g, u > u.

Отметим, что альтернативный запрет справедлив не только для основных частот, но и для любых переходов между колебательными уровнями молекул, обладающих центром симметрии. Для молекул в газовой фазе альтернативный запрет выполняется строго, для иных молекул (в жидкостях, газах) не строго, могут наблюдаться его нарушения. Частоты интенсивные в ИК-спектрах, могут давать слабые линии в КР, и наоборот.