Стационарные состояния квантовых и классических систем

Покажем, что для любой квантовой или классической системы, обладающей центральной симметрией и заданной энергией, существует такая метрика (5), что действие системы будет связано с некоторым решением уравнения поля (6). Уравнение Гамильтона-Якоби в метрике (5) имеет вид.

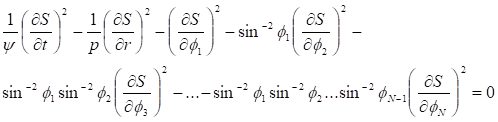
Уравнение (29) можно проинтегрировать при некоторых предположениях, используя метод Шредингера [22−23]. Суть метода состоит в том, чтобы представить решение уравнения (29) в виде Здесь в теорию в явном виде вводится классическое действие —, постоянная Планка и волновая функция. Используя классическое действие, мы определяем те параметры задачи, которые могут считаться внешними для квантовой системы. В случае метрики (5) удобно будет выбрать в качестве переменных квантовой механики углы на единичной сфере, а в качестве координат классического действия — время и радиальную координату. Тогда уравнение (29) разделяется на два уравнения.

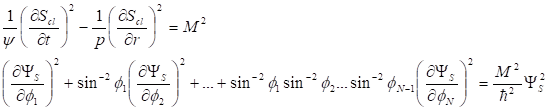
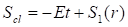
Здесь — произвольная постоянная, связанная с угловым моментом системы. В случае стационарных состояний действие системы можно представить в виде. Используя первое уравнение (31) и первый интеграл уравнения (6) в статическом случае, находим [3].

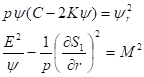
Выразим из первого уравнения (32) и подставим во второе, тогда получим.

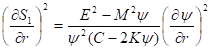
Очевидно, что решения уравнения (33) при всех вещественных значениях параметров и метрики определены в комплексной плоскости. Действительно, уравнение (33) можно представить в виде.

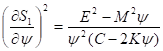
Отсюда следует, что функция действия в общем случае либо является комплексной, либо движение ограничено условием.

Поскольку же метрика допускает любые движения, то отсюда следует, что функция действия является комплексной. Разрешая уравнение (34), находим в явном виде зависимость действия стационарных систем от метрики, энергии, углового момента и химического потенциала, с которым параметр связан в силу (27) соотношением. Здесь знак + соответствует бозонам, а противоположный знак — фермионам. Таким образом, имеем.

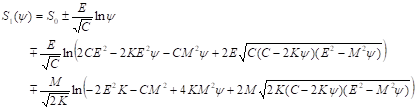
Здесь логарифмическая функция определена в комплексной плоскости, — произвольная постоянная.

В случае решение уравнения (34) имеет вид.

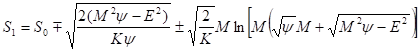
Полученные зависимости (36)-(37) решают поставленную задачу. Таким образом, мы доказали, что действие любой механической системы — классической или квантовой, находящейся в стационарном состоянии, зависит от параметров, характеризующих движение и от метрики окружающего пространства. Следовательно, для каждого типа движения существует такое уравнение состояния, что движение полностью определяется метрикой и параметрами движения — энергией и угловым моментом, что и требовалось доказать.

Отметим, что зависимость действия от параметров метрики в форме (36) является аналогичной логарифмической зависимости энтропии и коэффициента эмерджентности от числа состояний в форме (11), (17) и (25). Действительно, в статистической физике распределение типа (12) возникает в такой системе, в которой достигается экстремум энтропии. В гравитационном поле аналогичное распределение (27) возникает в системе обладающей центральной симметрией и метрикой, согласованной с метрикой Шварцшильда. Оба этих свойства, как известно, соотносятся со свойствами материи. Всякая же материальная система движется так, что действие и энтропия достигают экстремума.

Однако выражение действия (36) не зависит от предположений о виде функции, так как получено из более общих уравнений (32). Уравнение (36) описывает действие любой механической системы, в которой можно разделить действие для орбитального и радиального движения согласно (31).

Используя (36) можно определить действительную и мнимую часть действия для бозонов и фермионов в зависимости от параметров, описывающих влияние химического потенциала и размерности пространства соответственно — рис. 1. В случае фермионов действие достигает экстремума при размерности пространства равной 4, при этом. В случае же бозонов существует ряд локальных экстремумом, которые позволяют оптимизировать действие при любой размерности пространства — рис. 2. Это свойство действия бозонов сохраняется и при изменении энергии и момента системы — рис3−4.

Заметим, что случай является особенным для обсуждаемой модели, так как имеем, согласно (7),, что соответствует пустому плоскому пространству. Следовательно, в уравнении (6) положим. Отсюда находим.

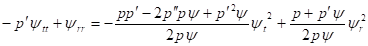
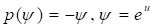
В частном случае, полагая в уравнении (38), имеем уравнение Лапласа.

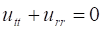
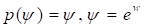
В другом частном случае, полагая в (38), приходим к волновому уравнению.

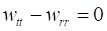
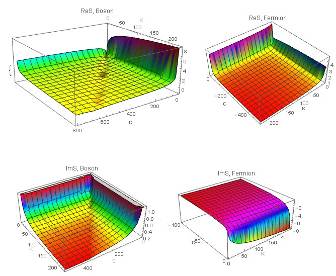
Рис. 1. Действительная (вверху) и мнимая (внизу) часть действия для бозонов и фермионов в зависимости от параметров .

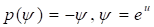
Рассмотрим динамику частиц в частном случае, когда уравнения поля сводятся к уравнению Лапласа (39). Решение уравнения (39), описывающее N центров гравитации на плоскости имеет вид.

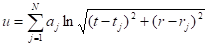
Было показано [4−5, 29], что аналогичная модель может быть получена в 6D в метрике Здесь — углы на единичных сферах, погруженных в трехмерные пространства; - координаты, связанные со временем и расстоянием соответственно.

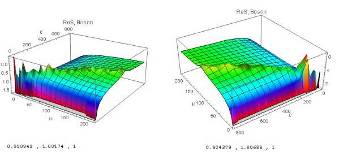
Рис. 2. Локальные экстремумы действительной части действия бозонов.

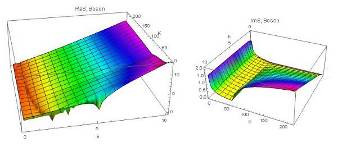
Рис. 3. Действительная и мнимая части действия бозонов в зависимости от параметров .

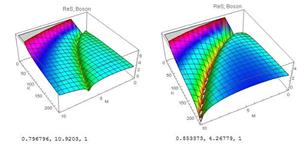
Рис. 4. Действительная часть действия бозонов в зависимости от параметров, вычисленная по (36) для (слева) и для (справа).

Действие в случае приводится к виду.

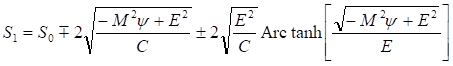
В этом случае действие также зависит логарифмически от параметров (с учетом свойств функции), однако метрика (41) также зависит логарифмически от координат источников, что позволяет сопоставить движение частиц на гиперсфере с радиальным движением в 6D и в 3D [4−5].

Таким образом, мы рассмотрели логарифмический закон в различных физических моделях — в статистике и в общей теории относительности в многомерных пространствах. Представляется интересным исследовать влияние логарифмических потенциалов на закономерности распознавания в задачах астросоциотипологии [37]. Такие задачи в астрологии, видимо, рассматривал Непер [1], так как он табулировал функцию, фигурирующую в уравнении (8,а). Однако изучение этих вопросов выходит за рамки настоящей работы.