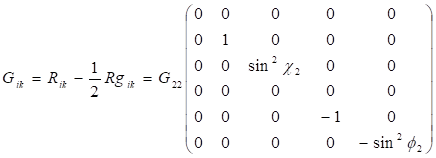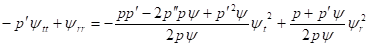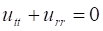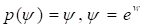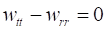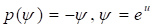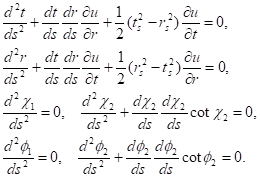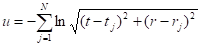Динамика частиц в 6D

В шестимерном пространстве с сигнатурой метрики можно построить естественное обобщение метрики (5) на случай наличия двух центров симметрии в виде [6].

(9).

Здесь — углы на единичных сферах, погруженных в трехмерные пространства; - координаты, связанные со временем и расстоянием соответственно.

Рассмотрим гравитацию в пространствах с метрикой (9). Заметим, что только четыре компоненты тензора Эйнштейна в метрике (9) отличны от нуля:

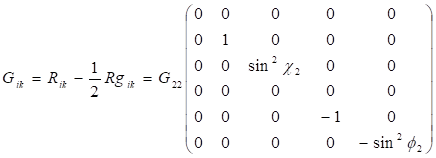
(10).

Следовательно, в этом случае в первом уравнении (1) следует положить, тогда уравнения поля в метрике (9) сводятся к одному уравнению второго порядка. Отсюда находим.

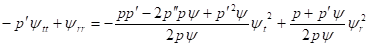
(11).

В частном случае, полагая в уравнении (11), имеем уравнение Лапласа.

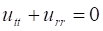
(12).

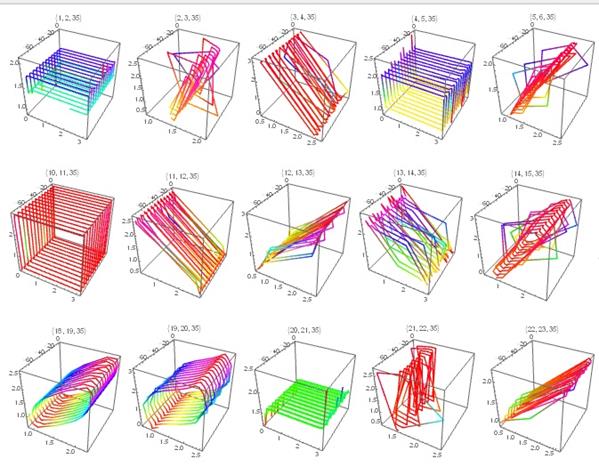
Рис. 1. Отображение движения на гиперсфере в трехмерном пространстве для N=35: над рисунками указаны комбинации углов, использованных для отображения.

В другом частном случае, полагая в (11), приходим к волновому уравнению [6].

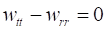
(13).

Рассмотрим динамику частиц в метрике (9) в частном случае, когда уравнения поля сводятся к уравнению Лапласа (12). В этом случае система уравнений (4) приводится к виду.

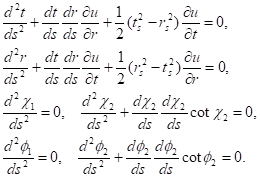
(15).

Здесь обозначено .

Решение уравнения (12), описывающее N центров гравитации на плоскости имеет вид.

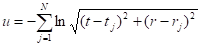
(16).

Из уравнений (15) видно, что движение в 6D в метрике (9) разделяется на движение на двух сферах и на движение в плоскости. В качестве координаты времени может быть выбран любой из углов или параметр — рис. 2−3.

На рис 2−3 представлены зависимости радиальных координат от параметра, траектории плоского и трехмерного движения в метрике (9) с потенциалом (16) с числом. Отметим, что в этих примерах 35 центров гравитации расположены равномерно по окружности радиуса 4, описанной вокруг точки .

Отметим сходство траекторий представленных на рис. 2−3 и на рис. 1. Это сходство обусловлено сходством динамических моделей (8) и (15)-(16). В системе уравнений (8) есть особые точки, где, при этом. В системе (15)-(16) этим точкам соответствуют логарифмические особенности функции .

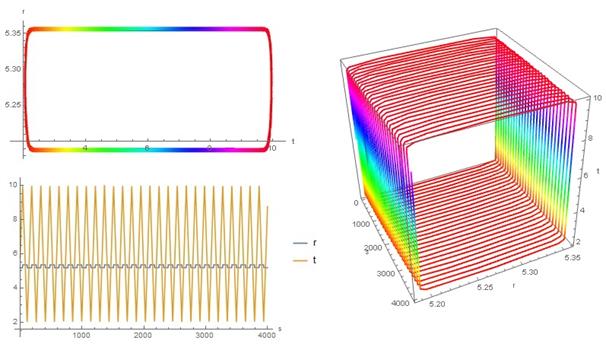
Рис. 2. Зависимость координат от параметра, траектории плоского и трехмерного нерелятивистского движения в 6D в метрике (9) с потенциалом (16) для .

Отметим, что в модели (15)-(16) различаются случаи нерелятивистского и релятивистского движения, которые соответствуют начальным данным и на рис 2−3. В первом случае траектории сгущаются вокруг сторон прямоугольника в плоскости, а во втором случае заполняют область ограниченную сторонами параллелограмма — рис. 3.

Рис. 3. Зависимость координат от параметра, траектории плоского и трехмерного релятивистского движения в 6D в метрике (9) с потенциалом (16) для .