Регрессионная модель. 
Влияние социально-экономических факторов на электоральное поведение избирателей Урала и Приволжья (по результатам выборов в Государственную Думу 2011 года)

В данном исследовании большую роль играют модели регрессии, которые, отмечу, важны нам не сами по себе, но в интерпретации, даваемой предикторам.

Регрессия — модель зависимости объясняемой переменной от объясняющих переменных. Причем зависимость в модели линейной регрессии выражается линейно [Bluman, pp.551−552].

Парная регрессия — регрессии с одним предиктором. Модель парной линейной регрессии имеет следующий вид:

Y = b₀ + b₁x + e,.

где: Y — исследуемая (зависимая) переменная;

x — предиктор;

b₀ — константа;

b — коэффициент при предикторе;

е — ошибка.

Множественная регрессия — регрессия с несколькими предикторами. Модель имеет следующий вид:

Y = b₀ + b₁x₁ + … + b_nx_n + e,.

где: Y — исследуемая (зависимая) переменная;

x₁ … x_n — предикторы;

b₀ — константа;

b₁ … b_n — коэффициенты при предикторах;

е — ошибка.

Предиктор (англ., «предсказатель») — параметр (независимая переменная), использующаяся для предсказания значений зависимой переменной в модели регрессии [Bluman, pp.551−552].

Для построения модели множественной регрессии будет использована процедура пошагового анализа, в котором предикторы пошагово включаются в модель. На первом шаге в модель включается тот предиктор, который оказывает самое большое влияние на исследуемую переменную среди всех прочих. На втором шаге — следующая по силе оказываемого влияния. При этом добавление нового предиктора не обязательно существенно изменит значение коэффициента детерминации. В такую модель могут войти не все предикторы, что обусловлено тем, что сами предикторы могут быть связаны друг с другом. Пошаговое включение будет строить столько моделей регрессии, сколько предикторов включается в модель. Конкретно в этом исследовании рассматривается модель с наибольшим числом включенных переменных.

Порядок построения такой модели следующим:

• 1) Подбор модели (вид связи — в данном случае — линейный);
• 2) Оценка параметров модели (расчет неизвестных коэффициентов);
• 3) Анализ адекватности модели (R² — коэффициент детерминации, F-статистика, анализ остатков) [Тюрин, Макаров, с.236−238].

Для оценки неизвестных коэффициентов применяется метод наименьших квадратов, который заключается в подборе таких коэффициентов b₀ и b₁, при которых квадраты остатков будут минимальны.

Приведем формулы, необходимые при расчете МНК (на примере парной регрессии):

.

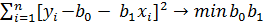
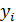
где: — истинное значение;

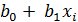
— предсказанное значение.

Таким образом, МНК-оценками для коэффициентов будут:

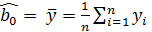
и.

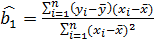
Полученные значения являются оценками неизвестных коэффициентов, которые попадают в конечную модель.

Для проверки качества (адекватности) полученной регрессионной модели используем F-критерий Фишера. Из всех различных методов расчета F-критерия предлагается работать со следующим:

.

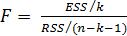
где: ESS (estimate sum of squares) — объясненная сумма квадратов,.

RSS (residual sum of squares) — сумма квадратов остатков,.

k — число объясняющих переменных,.

n — число наблюдений.

Если полученное значение F < F_crit, то это значит, что модель хорошая, а ее параметры подлежат дальнейшей адекватной интерпретации.

Еще немало важным критерием для оценки полученных результатов является коэффициент детерминации. Он показывает, какую долю значений исследуемой переменной способна объяснить модель.

.

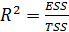
где: TSS (total sum of squares) — общая сумма квадратов.

Также при построении регрессионных моделей одним из важных моментов является анализ остатков, которая отвечает на вопрос: насколько хороша подобранная регрессионная модель. Теоретически в качественных моделях предполагается, что остатки будут вести себя как независимые одинаково распределенные случайные величины, желательно подчиняющиеся нормальному закону распределения. Для проведения анализа остатков можно использовать такие инструменты, как гистограмма частот, критерий Колмогорова-Смирнова.

Независимость остатков же проверяется при помощи критерия Дарбина-Уотсона, который позволяет определить наличие автокорреляций. Автокорреляция симптомизирует о том, что остатки в регрессионной модели достаточно сильно взаимозависимы, что существенно сказывается на качестве построенной модели. Само значение критерия варьируется по шкале от 0 до 4, при этом, полному отсутствию автокорреляций будет соответствовать значение 2.

При интерпретации полученных моделей регрессии будет уделяться внимание в первую очередь выявленным факторам, оказывающим влияние на значение, принимаемое зависимыми переменными. Значение, принимаемое коэффициентами при факторах, в этом случае способно дать представление о том, насколько сильно данный предиктор может повлиять на исследуемую переменную.

Стратегия исследования

Для успешного выполнения поставленной цели необходимо выработать стратегию работы с данными. Предполагаются следующие этапы в исследовании:

• 1) Этап описательных статистик;
• 2) Изучение нехарактерных значений с помощью диаграмм;
• 3) Расчет коэффициентов корреляции между исследуемой переменной и предикторами, определение значимых коэффициентов для включения предикторов в модель;
• 4) Построение моделей регрессии.

Последовательное выполнение перечисленных этапов позволит выполнить задачи исследования, проверить поставленные гипотезы и достигнуть цели, обозначенной во введении.

Выводы по главе 2

Здесь были описаны те статистические методы, которые используются в данном исследовании. При этом было указана не только формальное определение, но и методика расчета, которая позволит, при необходимости, вручную проверить полученные результаты. Теперь можно переходить к непосредственному статистическому анализу имеющихся у исследователя данных для проверки гипотез.

социальный экономический электоральный урбанизация.